hazy的leetcode刷题笔记(五)

leetocde.48:旋转图像-每日一题
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像

class Solution {
    /*基本思路：先存储第i行第j个元素，然后将第j行n - i个元素赋值给它。
    然后将第n - i行n - j个元素赋值给第j行n - i个
    以此类推
    */
    public void rotate(int[][] matrix) {
        int length = matrix.length;
        for(int i = 0; i < length / 2; i++) { //行
            for(int j = 0; j < (length + 1) / 2; j++) {//列
                int temp = matrix[i][j];
                matrix[i][j] = matrix[length - j - 1][i];
                matrix[length - 1 - j][i] = matrix[length - 1 - i][length - 1 - j];
                matrix[length - i - 1][length - j - 1] = matrix[j][length - i - 1];
                matrix[j][length - i - 1] = temp;
            }
        }
    }
}

leetocde.15:三数之和-hot100
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。
注意：答案中不可以包含重复的三元组。
示例：
给定数组 nums = [-1, 0, 1, 2, -1, -4]，
满足要求的三元组集合为：
[
[-1, 0, 1],
[-1, -1, 2]
]

class Solution {
    public List<List<Integer>> threeSum(int[] nums) { 
        /*基本思路：这种题很明显是首先要进行排序。原本的想法是用固定一个数，另外两个数去查哈希表，但是这样的话太复杂了
        于是使用双指针。当前数和后面两数加起来，如果大于0就移动右指针，小于0就移动左。
        等于0就加入结果集。此时，左右指针如果存在下一个数字相同，就需要继续移动左右指针直到不同
        */
        Arrays.sort(nums);
        List<List<Integer>> result = new ArrayList<>();
        int length = nums.length;
        for(int i = 0; i < length - 2; i++) {
            //当数字大于0时，由于左右指针的数肯定大于它，于是三者肯定大于0，直接返回
            if(nums[i] > 0) return result;
            //当前数跟前一个一样，就可以直接跳过了
            if(i > 0 && nums[i] == nums[i - 1]) continue;

            //左：相对于当前数字的下一个数字    右：最末尾的数字
            int left = i + 1, right = length - 1;
            while(left < right) {
                //如果等于0
                if(nums[i] + nums[left] + nums[right] == 0) {
                    //添加
                    List<Integer> temp = new ArrayList<>(3);
                    temp.add(nums[i]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    result.add(temp);
                    //存在左指针下一个数等于当前左指针所指的数，就移动左指针。右指针同理。
                    //移动结束后左指针指的是最后一个相同的数
                    while(left < right && nums[left + 1] == nums[left]) left++;
                    while(left < right && nums[right - 1] == nums[right]) right--;
                    //再次移动，此时左指针指的是与上一次所指不同的数了。比如左指针所指是 1 2 2 2 3
                    //那么第一次是在第一个2，经过上面的while就指向第三个2
                    //接下来就是在3
                    left++;
                    right--;
                }
                //如果大于0，移动右，下面同理
                else if(nums[i] + nums[left] + nums[right] > 0) {
                    right--;
                }
                else {
                    left++;
                }
            }
        }
        return result;
    }
}

leetocde.4:寻找两个正序数组的中位数
给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。
进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

//解法一：依次去两个数组中比较小的一个，取到第n/2个，但是需要判断奇偶
        int length_1 = nums1.length;
        int length_2 = nums2.length;
        int length = length_1 + length_2;
        int left = Integer.MIN_VALUE; 
        int right = Integer.MIN_VALUE;
        int start_1 = 0, start_2 = 0;
        for(int i = 0; i <= length / 2; i++) {
            left = right;
            if(start_1 < length_1 && (start_2 >= length_2 || nums1[start_1] < nums2[start_2])) {
                right = nums1[start_1++];
            }  
            else {
                right = nums2[start_2++];
            }
        }
        if((length & 1) == 0) {
            return (left + right) / 2.0;
        }
        else {
            return right;
        }

第二种解法：二分(官方题解的视频，讲得很好)

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        //思路：官方题解的视频，使用分割线来把两个数组分开，使得数组1和数组2的左边部分加起来等于n/2
        //把较短的数组赋给nums1，防止越界
        if(nums1.length > nums2.length) {
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;
        }
        int m = nums1.length;
        int n = nums2.length;
        //左边数组加起来的元素个数
        int totalLeft = (m + n + 1) / 2;

        int left = 0;
        int right = m;

        while(left < right) {
            //i为较短数组的下标 j为长数组的下标
            int i = left + (right - left + 1) / 2;
            int j = totalLeft - i;
            //当第一个数组分割线左边大于第二个数组分割线右边时，说明此时的划分不符合，缩小范围
            if(nums1[i - 1] > nums2[j]) {
                right = i - 1;
            } else {//同理 缩小范围
                left = i;
            }
        }

        int i = left;
        int j = totalLeft - i;
        int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];
        int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];
        int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];
        int nums2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];

        if (((m + n) % 2) == 1) {
            return Math.max(nums1LeftMax, nums2LeftMax);
        } else {
            return (double) ((Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin))) / 2;
        }  
    }
}

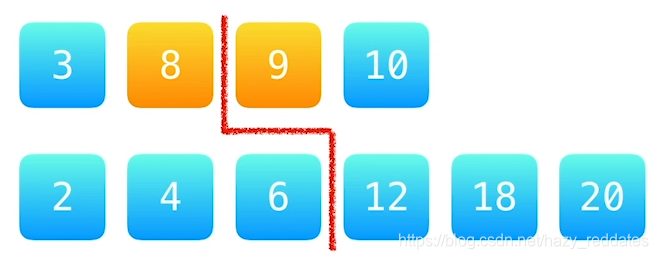
leetcode103:二叉树的锯齿形层序遍历
给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        /*基本思路：有点蠢的做法，就是根据左右依次交替，把节点添加到链表的最左或是最右进行遍历
        后面发现可以是跟普通层序遍历一样，只需要添加元素的时候添加到头或者尾就可以
        */
        LinkedList<TreeNode> record = new LinkedList<TreeNode>();
        List<List<Integer>> result = new ArrayList<>();
        if(root == null) return result;
        record.offer(root);
        boolean left = true;

        while(!record.isEmpty()) {
            int length = record.size();
            List<Integer> tempList = new ArrayList<>();
            //如果是按从左往右就跟普通层序一样
            if(left) {
                for(int i = 0; i < length; i++) {
                    TreeNode temp = record.poll();
                    tempList.add(temp.val);
                    if(temp.left != null) record.addLast(temp.left);
                    if(temp.right != null) record.addLast(temp.right);
                }
                left = false;
            } else { //如果是右往左，就添加到第i个位置上
                for(int i = length - 1; i >= 0; i--) {
                    TreeNode temp = record.remove(i);
                    tempList.add(temp.val);
                    
                    if(temp.right != null) record.add(i, temp.right);
                    if(temp.left != null) record.add(i, temp.left);
                }
                left = true;
            }
            result.add(tempList);  
        }
        return result;
    }
}

leetcode.55:跳跃游戏-hot100
给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

class Solution {
    public boolean canJump(int[] nums) {
        //基本思路：从左往右遍历 如果找到第一个能到达终点的地方，就把这个点当作新的终点
        //接着往下找 直到退出循环 否则的话说明无法到达
        int length = nums.length;
        if(length == 0 || length == 1) return true;
        int now = length - 1;
        //now为当前的终点下标
        while(now > 0) {
            //临时记录终点下标
            int temp = now;
            for(int i = 0; i < now; i++) {
                if(nums[i] + i >= now) {
                    now = i;
                }
            }
            //如果下标没有改变说明到不了这个终点直接退出
            if(now == temp) {return false;}
        }
        return true;
        
    }
}

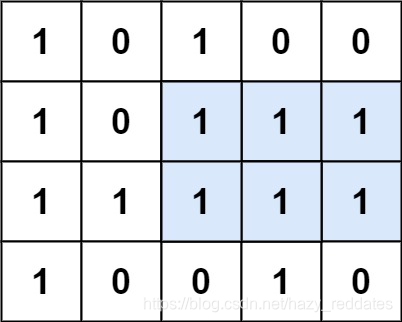
leetcode.85:最大矩形-每日一题
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

输出：6

class Solution {
    public int maximalRectangle(char[][] matrix) {
        //基本思路：先创建一个矩阵 对应位置存放对应行的连续个数，如：0 1 1 0存放为 0 1 2 0
        //接着将其转换为一个求以i j为右下角坐标的最大矩阵问题
        int row = matrix.length;
        if(row == 0) return 0;
        int col = matrix[0].length;
        int[][] continuous = new int[row][col];
        //创建对应的行连续记录数组
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                if(matrix[i][j] == '0') {
                    continuous[i][j] = 0;
                } else {
                    continuous[i][j] = j > 0 ? continuous[i][j - 1] + 1 : 1;
                }
            }
        }
        int result = 0;
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                //如果当前点为0说明其不能构成一个矩形
                if(continuous[i][j] == 0) {
                    continue;
                }
                //当前的最小长度
                int width = continuous[i][j];
                //当前的最大面积
                int area = width;
                for(int k = i - 1; k >= 0; k--) {
                    //取较短者
                    width = Math.min(width, continuous[k][j]);
                    //取面积较大者
                    area = Math.max(area, width * (i - k + 1));
                }
                result = Math.max(area, result);
            }
        }
        return result;

    }
}

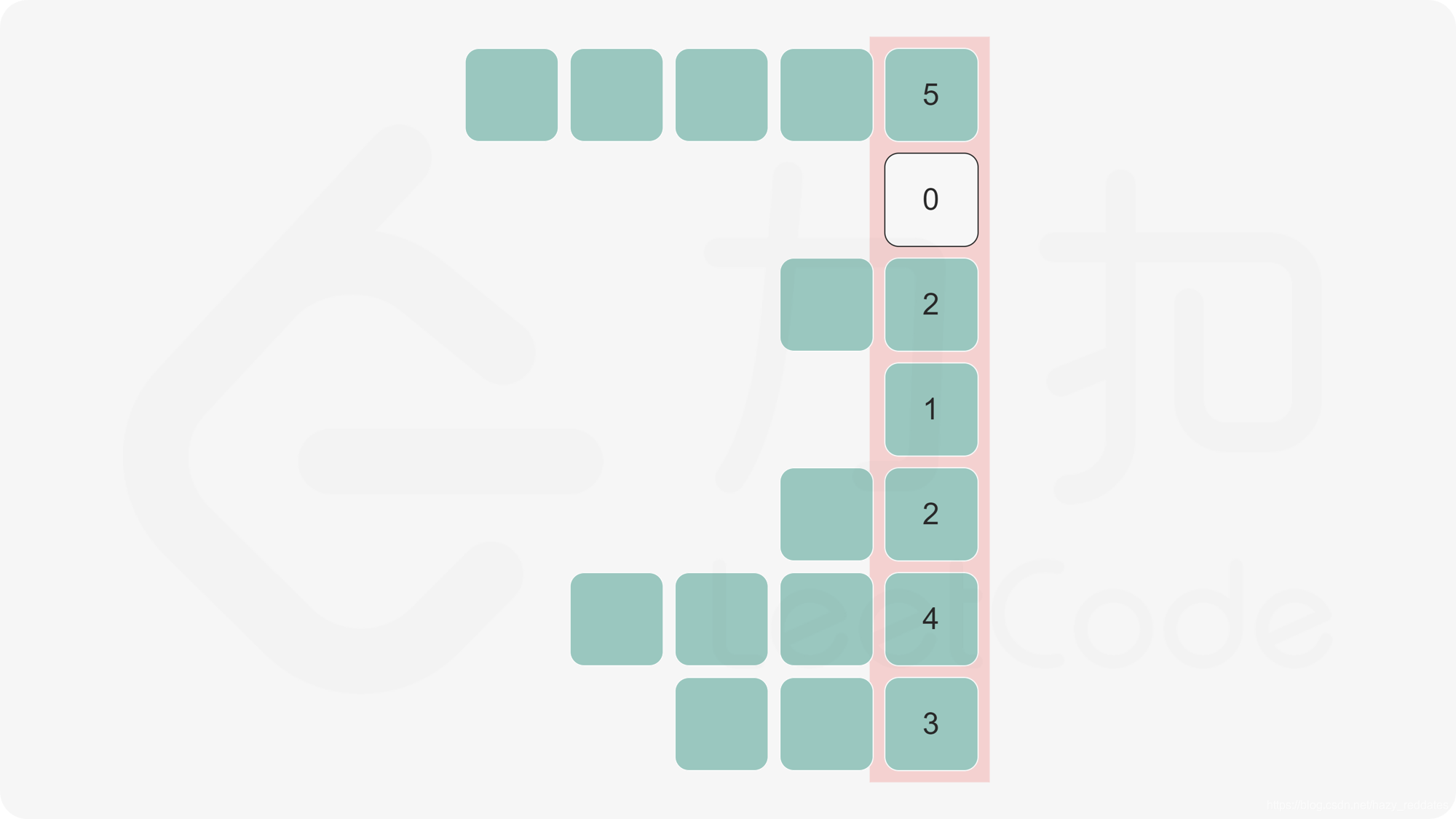
leetcode.84:柱状图中最大的矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

解法一：

class Solution {
    public int largestRectangleArea(int[] heights) {
        //基本思路：以当前柱子为右边界向左不断扩大取最大值
        int result = 0;
        for(int i = 0; i < heights.length; i++) {
            //当前柱子的面积
            int width = heights[i];
            int area = width;
            for(int j = i - 1; j >= 0; j--) {
                //往左进行扩大求面积
                width = Math.min(width, heights[j]);
                area = Math.max(area, (i - j + 1) * width);
            }
            //取最大值
            result = Math.max(result, area);
        }
        return result;
    }
}

解法二：

class Solution {
    public int largestRectangleArea(int[] heights) {
       // 这里为了代码简便，在柱体数组的头和尾加了两个高度为 0 的柱体。
        int[] tmp = new int[heights.length + 2];
        System.arraycopy(heights, 0, tmp, 1, heights.length); 
        
        Deque<Integer> stack = new ArrayDeque<>();
        int area = 0;
        for (int i = 0; i < tmp.length; i++) {
            // 对栈中柱体来说，栈中的下一个柱体就是其「左边第一个小于自身的柱体」；
            // 若当前柱体 i 的高度小于栈顶柱体的高度，说明 i 是栈顶柱体的「右边第一个小于栈顶柱体的柱体」。
            // 因此以栈顶柱体为高的矩形的左右宽度边界就确定了，可以计算面积🌶️ ～
            while (!stack.isEmpty() && tmp[i] < tmp[stack.peek()]) {
                int h = tmp[stack.pop()];
                area = Math.max(area, (i - stack.peek() - 1) * h);   
            }
            stack.push(i);
        }

        return area;
    }
}

leetcode.330:按要求补齐数组-每日一题

class Solution {
    public int minPatches(int[] nums, int n) {
        //基本思路：对于覆盖到[1, x)的区间，如果加上x就可以覆盖到[1,2x)
        //同理,对于已经覆盖到[1, x)的区间,再来一个数 a 只要它小于x,就可以覆盖到[1, x+a)
        //只需要判断数组中的下一个数是否大于x,如果是就说明要补充一个x,使区间能达到下一个数
        //如果小于就使区间变成[1, x+a) 直至满足x>n(因为是开区间所以要大于)
        long now = 1; //当前右边界
        int index = 0;
        int length = nums.length;
        int result = 0;
        while(now <= n) {
            //下一个数小于now就直接使区间变成[1, now + next)
            if(index < length && now >= nums[index]) {
                now += nums[index++];
            } else { //下一个数大于now就直接使区间变成[1, 2 * now)   result + 1
                now *= 2;
                result++;
            }
        }
        return result;
    }


}