Unet论文阅读笔记

Unet

论文链接：https://arxiv.org/pdf/1505.04597v1.pdf
github：https://github.com/milesial/Pytorch-UNet

Unet借鉴了FCN网络，其网络结构包括两个对称部分：前面一部分网络与普通卷积网络相同，使用了3x3的卷积和池化下采样，能够抓住图像中的上下文信息（也即像素间的关系）；后面部分网络则是与前面基本对称，使用的是3x3卷积和上采样，以达到输出图像分割的目的。此外，网络中还用到了特征融合，将前面部分下采样网络的特征与后面上采样部分的特征进行了融合以获得更准确的上下文信息，达到更好的分割效果.

网络概述

• 输入是572x572的，但是输出变成了388x388，这说明经过网络以后，输出的结果和原图不是完全对应的，这在计算loss和输出结果都可以得到体现.
• 蓝色箭头代表3x3的卷积操作，并且步长是1,不进行padding，因此，每个该操作以后，featuremap的大小会减2.
• 红色箭头代表2x2的最大池化操作.如果池化之前特征向量的大小是奇数，那么就会损失一些信息 。输入的大小最好满足一个条件，就是可以让每一层池化操作前的特征向量的大小是偶数，这样就不会损失一些信息，并且crop的时候不会产生误差.
• 绿色箭头代表2x2的反卷积操作.何为反卷积会在后面进行记录
• 灰色箭头表示复制和剪切操作.
• 输出的最后一层，使用了1x1的卷积层做了分类
• 前半部分也就是图中左边部分的作用是特征提取，后半部分也就是图中的右边部分是上采样
• 也叫 encoder-deconder结构

Over-tile策略

Unet的结构中没有全连接，这就表示Unet的输入图片的大小其实是可以不固定的。无论训练还是测试的时候，都可以放一整张图片进去。不过呢，通常来说，一张图片扔进去，对显存还是有一定挑战的，并且，Unet最开始是为了处理医疗图像的，一般医疗图像都非常大。

而over-tile策略可以使得任意大小输入的图片都可以获得一个无缝分割.

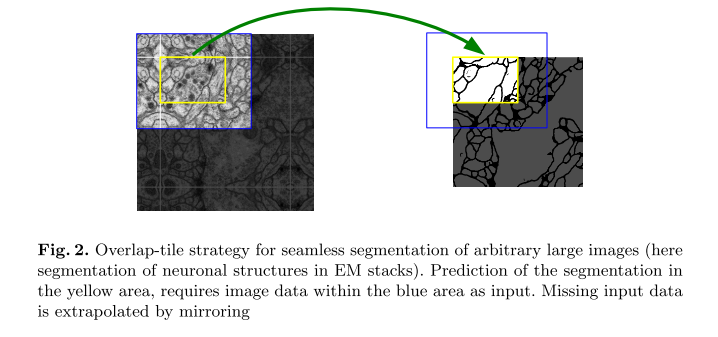
当对黄色部分进行预测的时候,需要该图像块周围的像素点(蓝色框内)提供上下文信息(context),以获得更加准确的预测.但是会出现两个问题.

• 边界的图像块是没有周围像素点的(不全).作者使用了一种镜像扩充的方式,对于没有周围的方向,沿图中的白色进行镜像扩充.
• 可能会导致土相重叠问题.即第一块和第二块会有部分重叠.作者通过不适用padding进行卷积的方法,(以及crop)消除这方面的影响(valid part of each convolution)

反卷积

• 上采样(Upsample)

在应用在计算机视觉的深度学习领域，由于输入图像通过卷积神经网络(CNN)提取特征后，输出的尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.:图像的语义分割)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)。

• 反卷积(Transposed Convolution)

上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：
反卷积是一种特殊的正向卷积，先按照一定的比例通过补 $0$来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

卷积输出尺寸计算

• 输入尺寸（input）：$i$
• 卷积核大小（kernel size）： $k$
• 步幅（stride）： $s$
• 边界扩充（padding）： $p$
• 输出尺寸（output）： $o$

$o=[\frac{i+2p-k}{s}+1]$

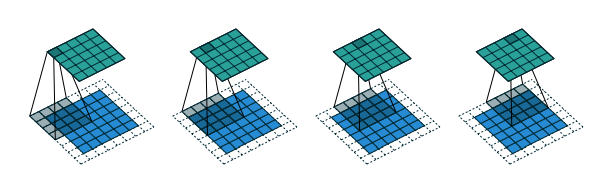
以图中为例:

$i=6,k=3,s=2,p=1,$

$o=[\frac{6+2\times 1-3}{2}+1]=3$

反卷积输出尺寸计算

• $(o+2p-k)\%s=0$

  $o=s(i-1)-2p+k$

• $(o+2p-k)\%s\ne 0$

  $o=s(i-1)-2p+k+(o+2p-k)$

数据增强

由于医学数据通常是非常少的，因此数据增强就变得异常重要。显微镜图像一般需要旋转平移不变性，弹性形变和灰度值变化鲁棒性。训练样本的随机性变形似乎是训练之后少量标注图像的分割网络的关键.因为在医学中,细胞发生弹性变化是时有的事情

$1\times 1$的卷积层

降维/升维

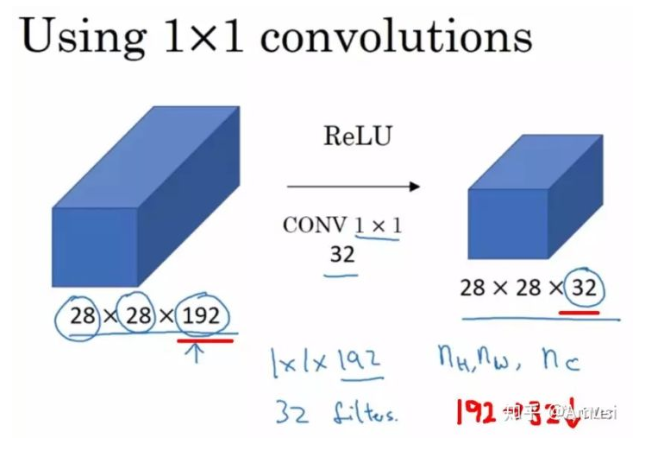
加入非线性。卷积层之后经过激励层，1*1的卷积在前一层的学习表示上添加了非线性激励（ non-linear activation ），提升网络的表达能力；

不足

• crop的原因并没有说明?不会损耗上下文信息嘛?

参考

反卷积输出尺寸计算公式

论文笔记：U-Net: Convolutional Networks for Biomedical Image Segmentation

Unet

A guide to convolution arithmetic for deep learning

一文读懂卷积神经网络中的1x1卷积核