平衡二叉树（AVL树）

1、什么是平衡二叉树

平衡因子（Balance Factor，简称BF）: BF(T) =h_L-h_R，
其中h_L和h_R分别为T的左、右子树的高度。

平衡二叉树（Balanced Binary Tree）（AVL树）：
空树，或者任一结点左、右子树高度差的绝对值不超过1，即|BF(T) |≤ 1

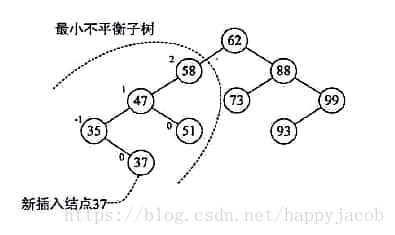
最小不平衡子树：距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树

设 n_h 高度为h的平衡二叉树的最少结点数。结点数最少时：

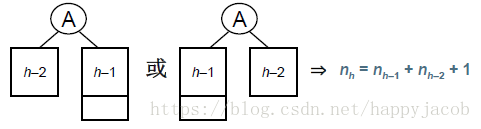
给定结点数为 n的AVL树的最大高度：O(log2n)！

2、平衡二叉树的调整

1、RR旋转：麻烦结点在发现者右子树的右边
注意：麻烦结点不一定是其父节点的右节点，也可能是左节点

2、LL旋转：麻烦结点在发现者左子树的左边
注意：麻烦结点不一定是其父节点的左节点，也可能是右节点

3、LR旋转：麻烦结点Jan在发现者May左子树的右边

4、RL旋转：麻烦结点Jan在发现者May右子树的左边

注意：有时候插入元素即便不需要调整结构，也可能需要重新计算一些平衡因子。