【文章阅读】【超解像】---Deep laplacian Pyramid Networks for Fast and Accurate Super-Resolution

【文章阅读】【超解像】–Deep laplacian Pyramid Networks for Fast and Accurate Super-Resolution

期刊论文CVPR2017链接：http://vllab.ucmerced.edu/wlai24/LapSRN/papers/cvpr17_LapSRN.pdf

项目主页：http://vllab.ucmerced.edu/wlai24/LapSRN/

本文为LapSRN的期刊论文解析，作者还对这个方法做了进一步优化，后续分析。

1.主要贡献

​ 本文主要工作如下：

​ 1). 提出一种拉普拉斯金字塔网络结构，每一级金字塔结构以粗糙分辨的图作为输入（低分辨率输入，很多方法是利用放大后的图像作为输入），用转置卷积进行升采样得到更精细的特征图;

​ 2). 利用robust Charbonnier loss function 作为损失函数；

​ 3). 一个网络结构可以实现多分辨率的放大，如一个放大8倍的模型可以同时实现2倍和4倍的图像放大。

2.论文分析

​ 1) 网络结构

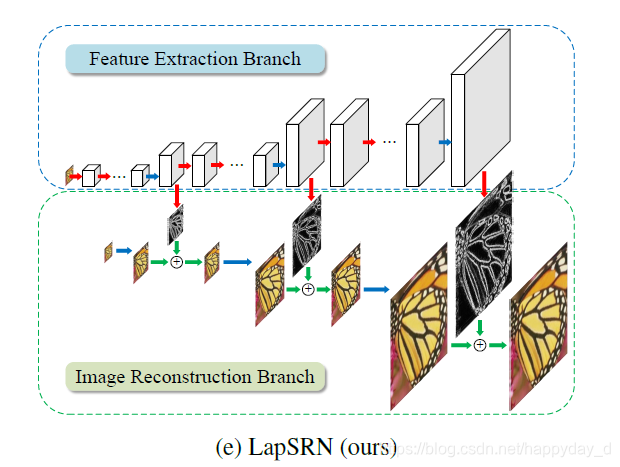
​ 分为特征提取结构和图像重建结构：

​ 特征提取结构：在第s层，特征提取网络结构有d个卷积层和一个转置卷积层，转置卷积层的作用是将提取的图像特征扩大2倍，转置卷积的输出有两个去处，一是图像重建结构的卷积层用来重建图像，一是特征提取的第s+1层；这种特征提取的好处为：直接从低分辨率图像提取图像特征，用一个转置卷积产生高分辨率的图像特征，这样降低的图像的计算复杂度，提起的低层特征作为金字塔的高层的输入，提高卷积网络的非线性，使网络结构可以学习到更复杂的特征；

​ 图像重建结构：在第s层，输入图像经过转置卷积放大2倍，与特征提取得到的高分辨率特征图相加，得到的输出作为高层图像重建结构的输入，整个网络结构是一个串联的CNN，每个层级都有相似的结构。

​ 2）损失函数
$$L(y,\hat{y},\theta )=\frac{1}{N}\sum _{i=1}^N\sum _{s=1}^L\rho (y_s^{(i)}-{\hat{y}}_s^{(i)})$$
​ 其中${\hat{y}}_s^{(i)}=x_s^{(i)}+r_s^{(i)}$ 表示网络结构中金字塔的第s层的输出，N表示一个patch的图像数量，L表示金字塔的层数，$y_s$ 表示真值图像，是真值通过降采样得到得到的。$r_s$ 表示特征提取结构经过转换卷积得到的输出，$x_s$ 表示输入图像放大后的图像。$\rho (x)=\sqrt{x^2+{\epsilon }^2}$ （l1范数的变体）

实验比较了本文提出的损失函数和L2损失函数的性能比较：

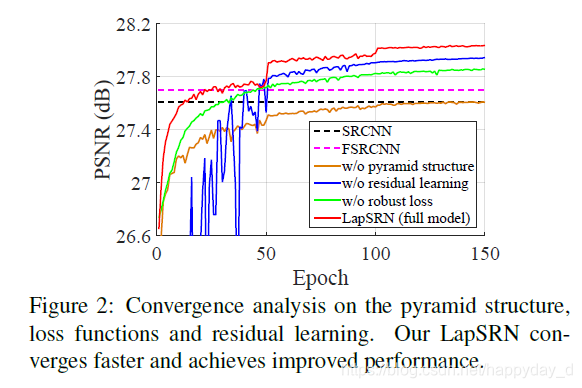
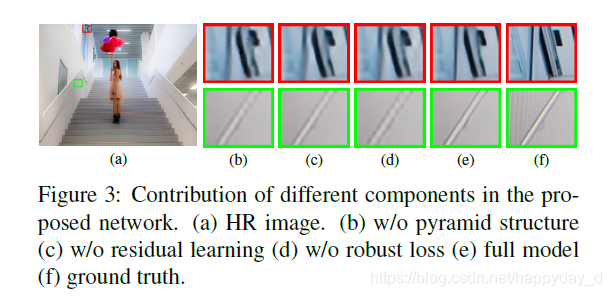
​ 图2中绿色是利用L2作为损失函数，需要更多的训练次数才能达到SRCNN的性能，从图3可看出带来了更多的人为伪像

​ 3) 训练细节

​ 每个卷积核都是$3\ast 3\ast 64$ ,转换卷积核大小为$4\ast 4$ ,激活函数使用的是LReLU，对2倍和4倍的放大，金字塔的每层卷积层为d=10,对8倍放大，d=5; 下表中不同的层数的性能和图像处理时间。

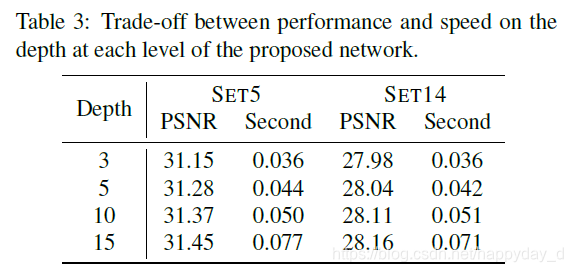
3.结果分析

​ 和之前的方法进行比较，性能如下，性能好，处理速度快。

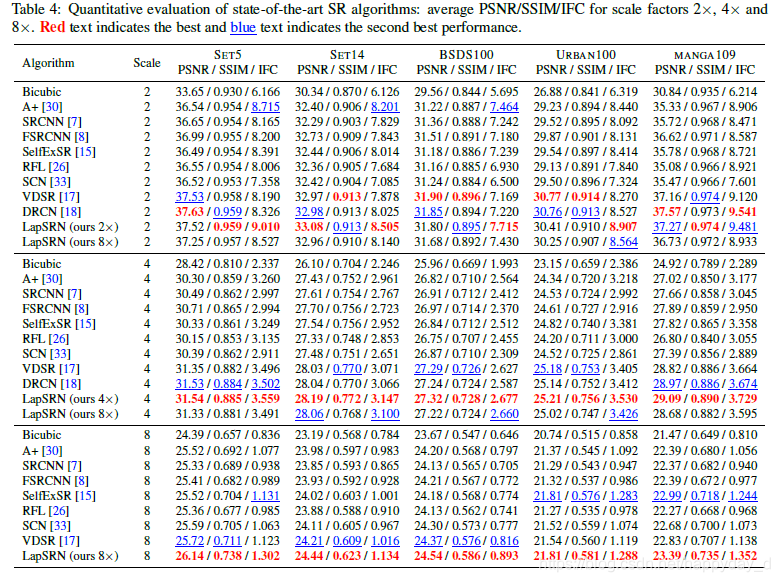
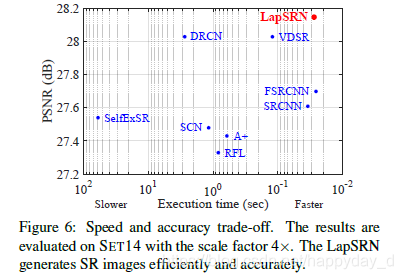
缺点，如下图，8倍放大过程中，图像细节不能正常恢复。

4.参考

https://blog.youkuaiyun.com/Cyiano/article/details/78519521

论文个人理解，如有问题，烦请指正，谢谢！