使用生存集成模型进行流失预测

I. 引言

近年来，随着社交网络和智能手机的普及，游戏经济发生了变化，催生了一种新型视频游戏：社交游戏。社交游戏面向的是新的玩家群体：休闲玩家，采用了一种新的货币化模式：免费增值（F2P或freemium），这种模式现在在所有移动平台上占据主导地位 [2], [14]。免费增值模式包括免费提供游戏，通过应用内购买收费来实现货币化。

对于社交游戏来说，玩家保留是成功货币化的关键，并且增加社交互动，从而帮助推动游戏的采用和保留玩家。此外，获取新玩家的成本不断增加 [14]，并且可能显著超过保留现有玩家的成本。

本研究的动机在于能够预测玩家何时会离开游戏，从而采取激励措施重新吸引他们并防止流失，或者将他们转移到公司的另一款游戏中。

流失预测在电信、金融、零售、付费电视和银行领域已经被广泛研究，如 [55], [58] 所示的广泛文献综述所示。它也在电子商务 [60], [61] 以及员工保留 [51] 方面进行了研究。

在视频游戏领域，开创性的研究在 [29], [31] 中提出。然而，他们主要关注的是MMORPG（大型多人在线角色扮演游戏）。MMORPG 是第一种成功的在线社交游戏类型，但它们针对的是更狭窄的受众，主要使用基于订阅的货币化模式。这意味着可以将流失测量为合同的正式终止，类似于上述提到的行业，除了电子商务之外。

免费增值（F2P）货币化是移动社交游戏使用的主要模式，涉及非合同关系。在这种情况下，流失不是通过明确声明终止合同来清楚地确定的。对于最活跃的玩家，我们可以将流失定义为长时间的不活跃。然而，这个问题与电子商务中的流失略有不同。实际上，不活跃的用户总是可以回到电子商务网站，而不活跃的移动玩家可以卸载游戏，这将对应于一个明确且最终的流失状态。然而，这些信息通常是不可用的。在非合同环境中流失的定义在 [10] 中进行了讨论。关于F2P应用程序流失定义的全面讨论超出了本文的范围，是专门研究的主题 [10]。

[19] 中提出的工作是第一个研究F2P游戏中流失预测的研究。[19] 介绍了问题的一般定义、一组独立于游戏内容的特征以及分类器的比较。[48] 中展示的第二项研究专注于F2P游戏中高价值玩家的流失预测。[48] 详细研究了问题定义和分类器评估，尽管它仅从二元分类的角度处理问题。它使用了一种假设数据分布的算法，这通常不符合流失数据的常见形态。进一步的，[49] 和 [47] 尝试解决移动游戏中流失预测的数据时间性问题。

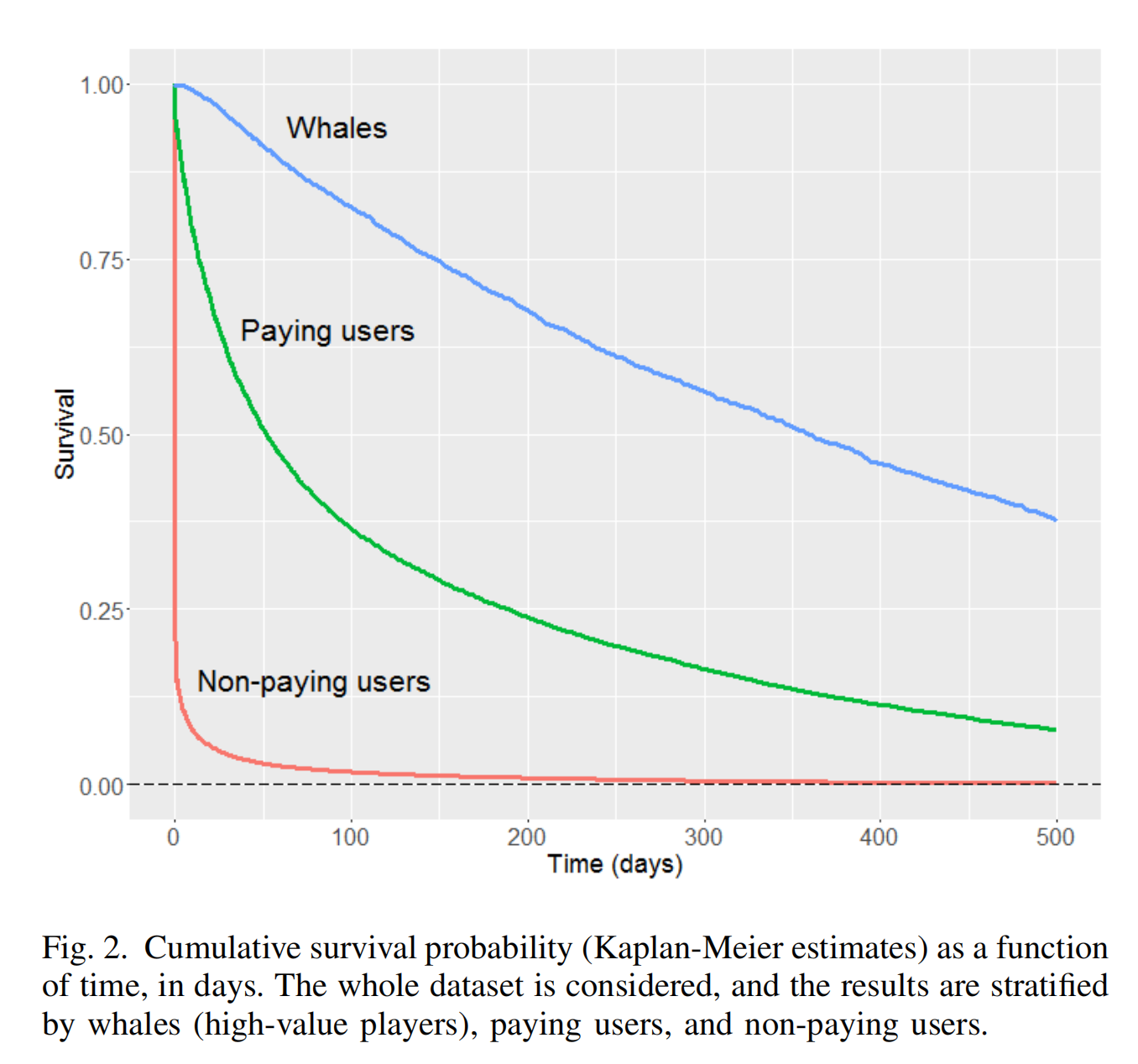
本文的工作重点是预测在视频游戏行业中通常称为鲸鱼的高价值玩家的流失。关注这一点的动机在于，鲸鱼的行为与普通玩家不同，包括他们的生存曲线，如图2所示。由于他们通常是最活跃的玩家，即几乎每天都玩，我们可以轻松地将他们的流失定义为长时间的不活跃。他们的高参与度还允许收集更多关于他们活动的数据，使他们更可能对采取的防止流失的措施作出积极回应。最后，从商业角度来看，鲸鱼玩家约占玩家的0.15%或付费用户的10% [28]，他们特别重要，因为他们是占应用内购买收入50%的顶级消费群体。

本研究选择的游戏是由Silicon Studio开发的《Age of Ishtaria》，它代表了成功的移动社交游戏，拥有数百万玩家。

A. 我们的贡献

传统的流失研究方法将问题视为二元分类：玩家是否再次连接到游戏（例如 [3]）。尽管二元模型非常直观，但它们无法预测玩家何时会停止玩游戏，此外，特征仅限于提供静态（非时间性）信息。

为了建模流失时间，传统方法如回归分析仅在所有玩家都停止玩游戏时才适用。对于包含每个用户不完整信息的数据，挑战在于一些用户仍在玩游戏。

本研究改进了之前的研究 [19], [48]，使用了一种适当的技术来处理截尾数据（关于流失时间的不完整信息的观察） [34]，并捕捉流失预测挑战的时间维度。

我们基于生存集成的模型输出了玩家流失时间的准确预测，并提供了影响玩家退出的风险因素信息。此外，本文建议的方法不仅给出了可能流失玩家的列表，还为每个玩家生成了一个生存概率函数，让我们知道流失概率如何随时间变化。这个特性使我们能够区分不同级别的忠诚度档案，即将流失、近期流失和远期流失，以及影响这种生存行为的变量（考虑到只要玩家连接到社交游戏，他们就被视为“存活”）。

从这个生存函数中提取出中位生存时间，并用作预期寿命阈值。这个特性使我们能够将玩家标记为有流失风险，提前采取行动保留有价值的玩家，并最终改进游戏开发以提高玩家满意度。

据我们所知，我们是第一个在社交游戏领域使用生存集成方法全面建模流失预测的人。我们的模型提高了传统生存方法（如Cox回归）的准确性、鲁棒性和灵活性，并且旨在在实际业务环境中可用。

II. 生存集成模型

A. 生存分析

生存分析由一组统计技术组成，传统上用于预测医学和生物研究中个体的预期寿命 [15], [26], [35]。这些方法也被应用于多个行业来预测客户流失，主要在电信 [36]、银行 [54] 和保险 [16] 领域。

生存分析专注于研究事件发生的时间及其与不同因素的关系。最初在医学研究中，事件是个体的失败或死亡，但在我们的案例中，它是玩家离开游戏的时刻。事件发生的时间也称为生存时间。

生存分析的一个基本特征是数据是截尾的。截尾表示观察结果不包括关于事件发生的完整信息。这意味着对于一定数量的玩家，我们不知道事件发生的时间（因为他们尚未经历），即测量值仅包含事件是否在给定时间 $t$ 之前发生的信息。

生存函数 $S(t)$，即玩家在某个时间 $t$ 存活的可能性，可以通过非参数的 Kaplan-Meier 估计器 [30] 来估计，其中流失概率可以直接从记录的截尾生存时间中计算出来。

如果在研究期间 $T$ 内 $k$ 个玩家在不同的时间点 $t_1<t_2<t_3\dots <t_k$ 流失，并且假设流失事件彼此独立 [9]，则可以通过从一个时间到下一个时间的存活概率相乘来获得累积存活概率：

$$S(t_j)=S(t_{j-1})\left(1-\frac{d_j}{n_j}\right)$$