吴恩达神经网络和深度学习课程自学笔记（九）之卷积神经网络

卷积神经网络

计算机视觉问题一般数据输入量非常大，因此难以获取足够的数据来防止神经网络发生过拟合以及很好的满足计算力/内存需求。解决这个问题就用到了卷积运算。

卷积运算

边缘检测问题

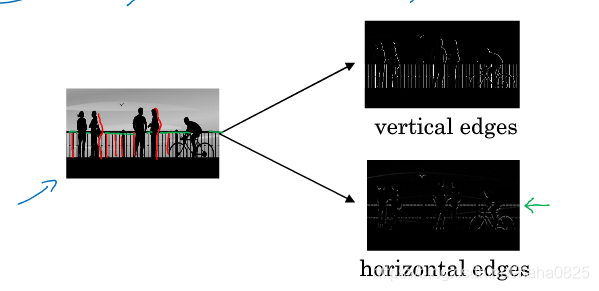
一般分为垂直边缘检测和水平边缘检测。

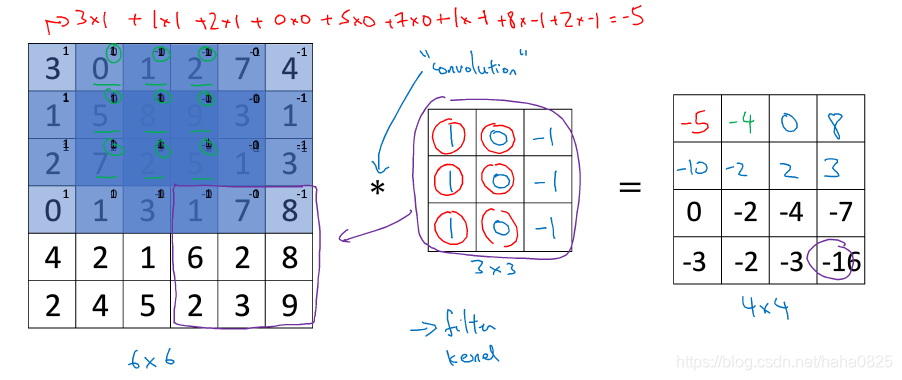
最左边的6*6为输入的一张图片，每个框内是它的每个像素点的值；中间的3行3列为过滤器，用于进行卷积运算；最右边为输出。

卷积运算过程：首先过滤器与图片的左上角做乘法，即
$$3\ast 1+0\ast 0+1\ast -1+1\ast 1+5\ast 0+8\ast -1+2\ast 1+7\ast 0+2\ast -1=-5$$

---

然后按照这种方式依次从左到右、从上到下每次移动一列/一行，直到图像的右下角，运算结束，结果是一个4*4的图像。通过改变过滤器的值即可实现水平/垂直边界检测。

垂直/水平边界检测在python中用conv_forward实现；在tf中用tf.nn.convzd实现；在Keras中使用Conv2D实现。

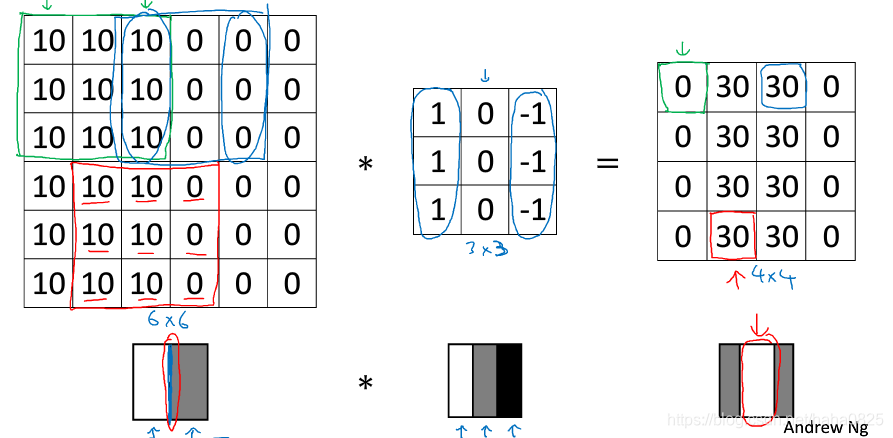
边缘检测区别正边和负边，即由亮到暗和由暗到亮的区别。

上图为垂直边缘检测，将过滤器进行翻转则就是水平边缘检测。

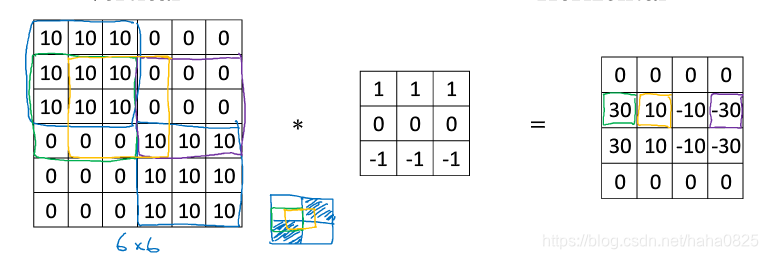
对于上面这种图像一般使用下面两个过滤器：

1	0	-1		3	0	-3
2	0	-2		10	0	-10
1	0	-1		3	0	-3

左边的为sobel过滤器，右边的为scharr过滤器。

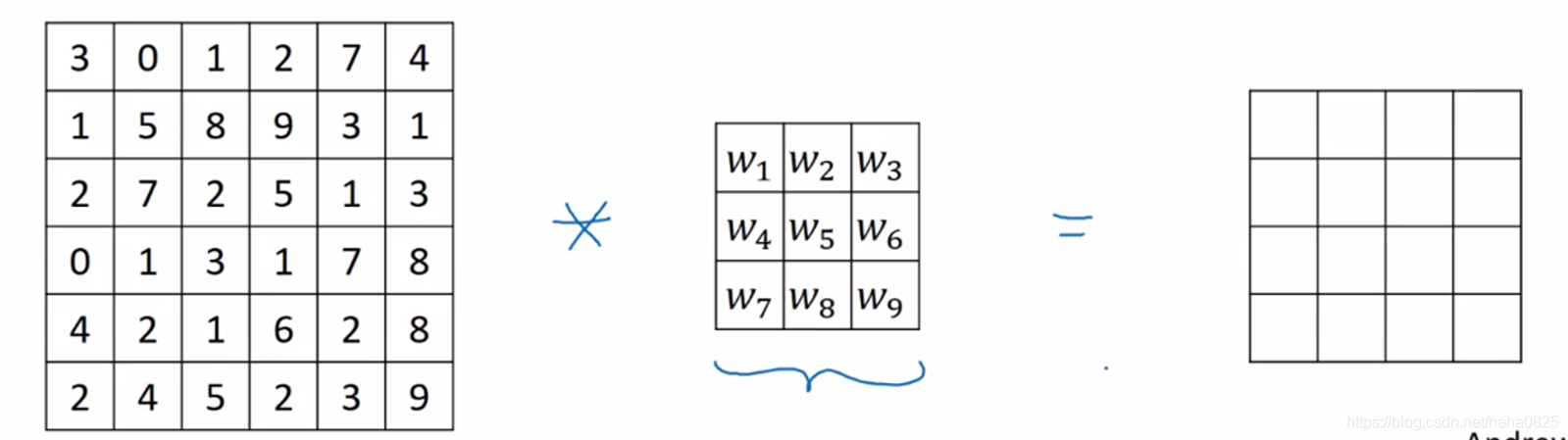
实际应用时可以设置这九个参数也可以为未知，我们可以通过反向传播算法学习出这九个参数。

padding（一个基本卷积操作—填充）

一个输入为n行n列的图像，经过与f行f列过滤器卷积运算后产生一个(n-f+1)*(n-f+1)的输出。这也体现了卷积操作的两个缺点：一是每次卷积后图像就会变小；二是中间部分重叠多，重复使用很多，而边缘部分像素点使用很少，这样会丢掉一些信息，甚至是比较重要的信息。

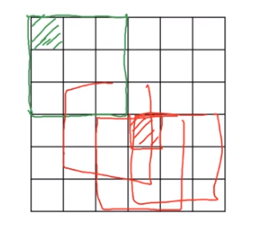
解决办法：在沿着图像边缘再填充一层像素，一般用0填充。

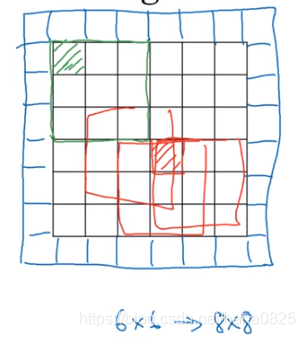
设p为填充的数量，（此时p等于1）则n行n列的输入经过卷积后输出为（n+2p-f+1）*（n+2p-f+1）

valid卷积和same卷积

valid：不填充

same：填充后使得输出大小和输入大小相同。即

$$n+2p-f+1=n==>p=(f-1)/2$$

计算机视觉问题中过滤器的p通常为奇数，若为偶数则会导致p不是整数，即填充后的图像左边多或右边多，左右不对称，因此通常建议过滤器的f为奇数。

卷积步长

前面我们都是一次移动一行/一列，这就是步长。

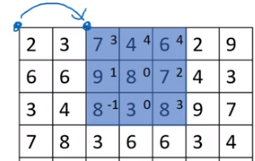
设步长为s，填充大小为p，则一个输入为n行n列的图像，经过与f行f列过滤器卷积运算后产生一个((n+2p-f)/s+1)*((n+2p-f)/s+1)的输出，若商不是整数，通常向下取整。因为过滤器必须处于图像中或填充后的区域内，此时才输出相应结果，所以向下取整。

卷积的工作方式

在RGB图像上

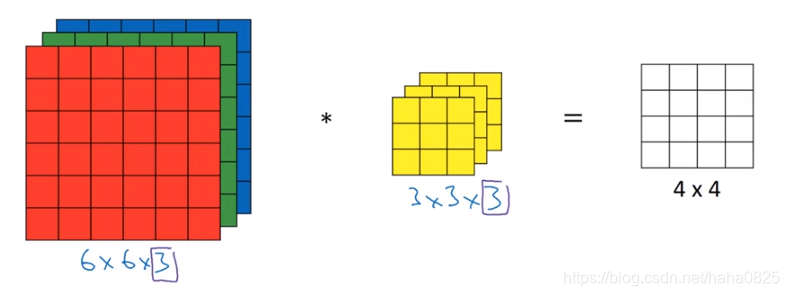
其中第三个数“3”为通道数，输入的通道数必须与过滤器的相同。

计算过程：与前面一个通道的类似，在这个立方体上，从左至右从上至下从前至后依次乘积并相加，直到最后一部分。

若想检测红色边缘，则过滤器应设置为：

R	R	R	G	G	G	B	B	B
1	0	-1	0	0	0	0	0	0
1	0	-1	0	0	0	0	0	0
1	0	-1	0	0	0	0	0	0

若检测整体的边界，则过滤器设为：

R	R	R	G	G	G	B	B	B
1	0	-1	1	0	-1	1	0	-1
1	0	-1	1	0	-1	1	0	-1
1	0	-1	1	0	-1	1	0	-1

多个过滤器的情况：假设有两个过滤器，一个水平边缘检测器一个垂直边缘检测器，分别卷积，得出的结果再组合在一起，即结果有两个通道。输出的通道数等于要检测的特征数。

单层卷积网络（构造）

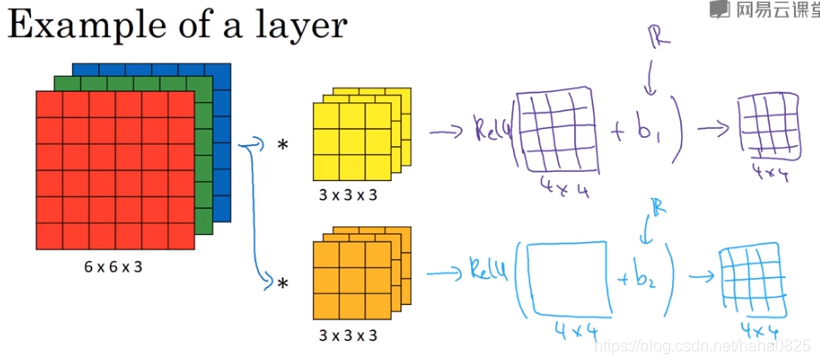
在输入图片与过滤器进行卷积操作后的输出后面加上激活函数等，就可以得到我们想要的输出。

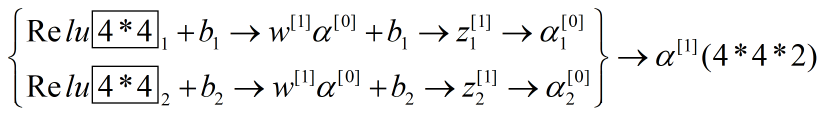
假设有10个3*3的过滤器，每个过滤器应该有3^3+1个，（1个是偏差b）即28个参数，总共是280个参数，无论输入多大，就这些参数，这也是卷积神经网络的特征，可以避免过拟合。

这些参数一一对应，就和我们前面的反向传播算法联系起来了。

卷积神经网络具体实例：

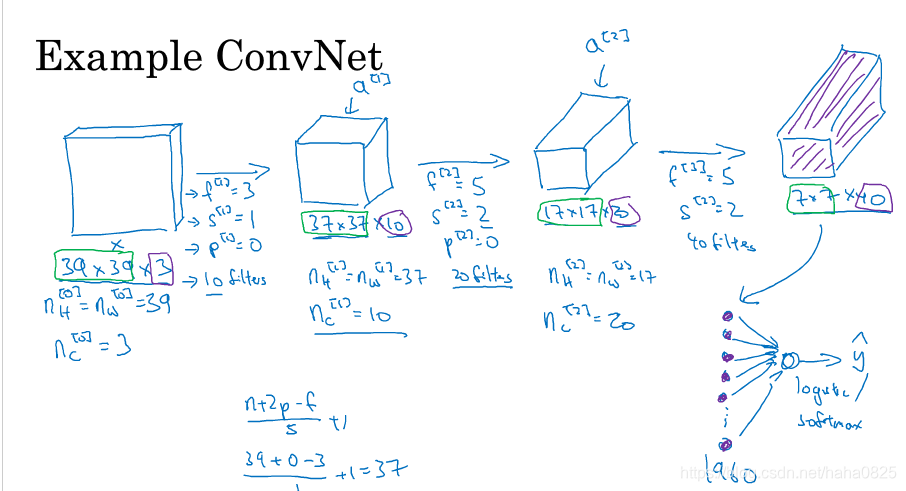
一般往右边来的过程，过滤器大小会变小，但是数量会变多。（因为步长变大了）

一个典型的卷积神经网络通常有三层：

（1）卷积层（CONV）

（2）池化层（POOL）

（3）全连接层（FC）

池化层

池化层作用：缩减模型大小，提高计算速度，提高所提取特征的鲁棒性。

1.最大池化

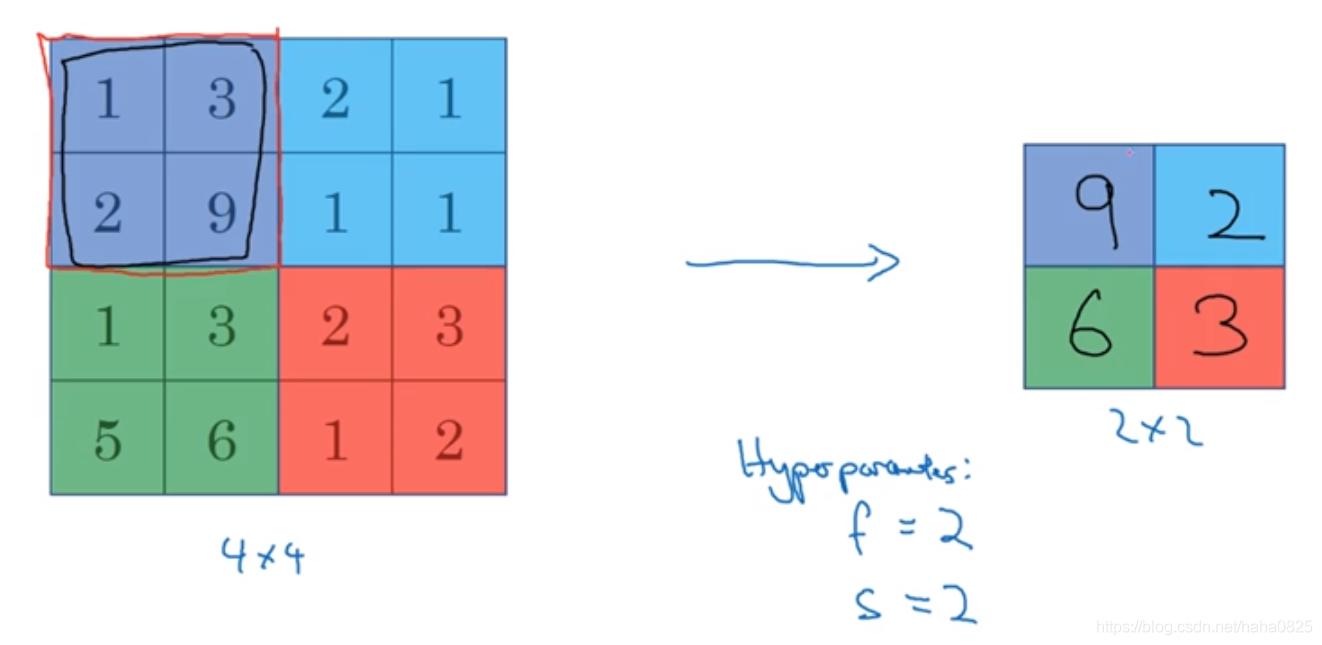
参数：过滤器大小为2*2，步长为2.

具体操作：只要在任何一个象限内提取到某个特征，他们都会保留在最大池化的输出里。即在过滤器中提取到某个特征，那么保留其最大值。

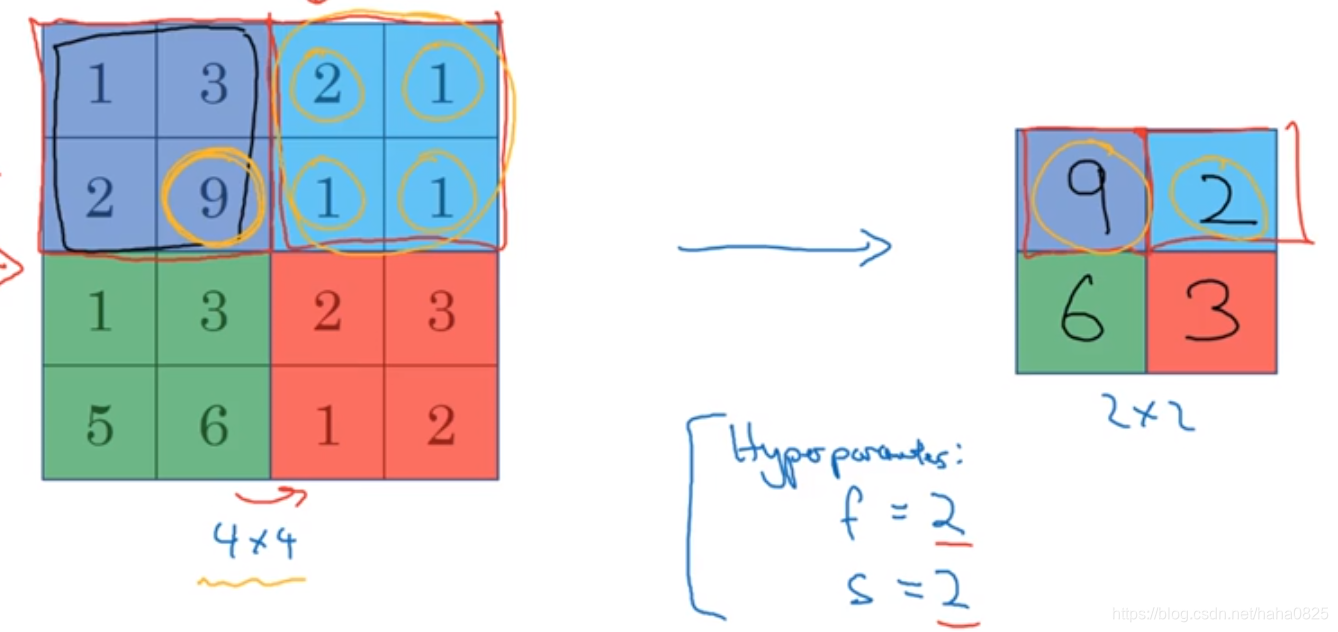
2.平均池化（不太常用）

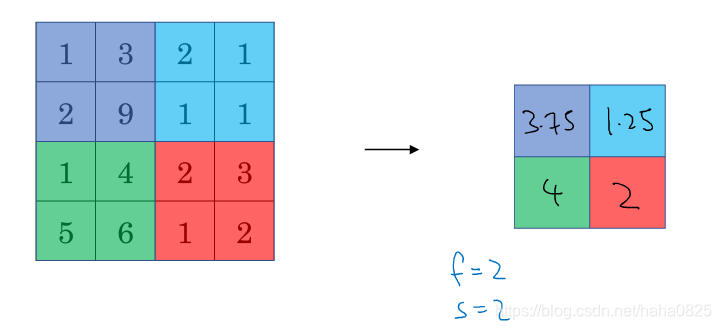
参数：过滤器大小为2*2，步长为2.

具体操作：取每个区域的平均值。

深度比较深的网络使用平均池化比较好。

池化层是没什么需要学习的参数，静态的。

全连接层

有时候统计层数只计算有权重的层（池化层参数固定不算一层）

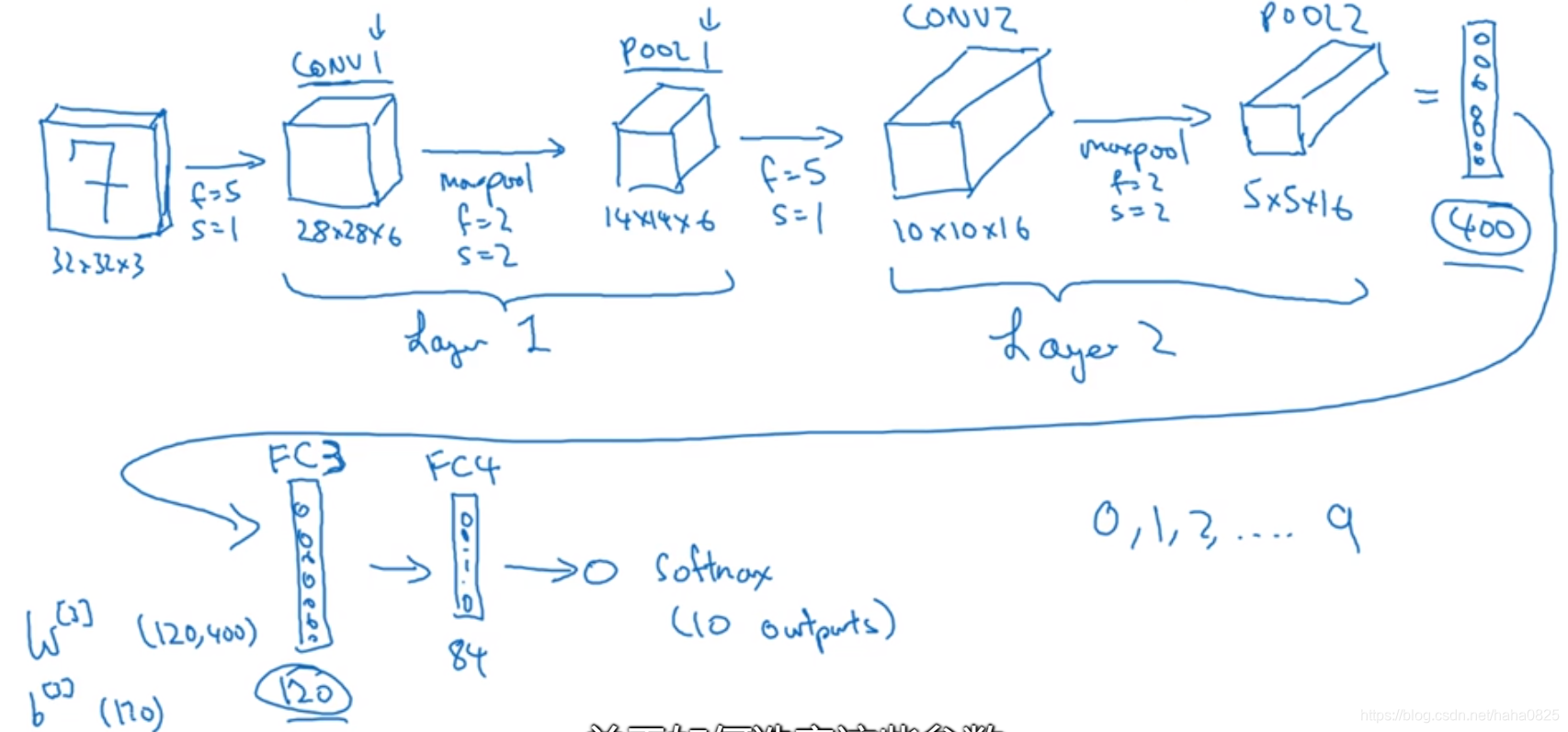
最后3层竖直排列的就是全连接层。从池化层输出的图像按像素点排成一列，然后做相应处理，最后根据softmax函数确定最终结果。

超级参数（f,s,p）尽量不要自己设置，要查看文献，看别人怎么设置，借鉴一下。

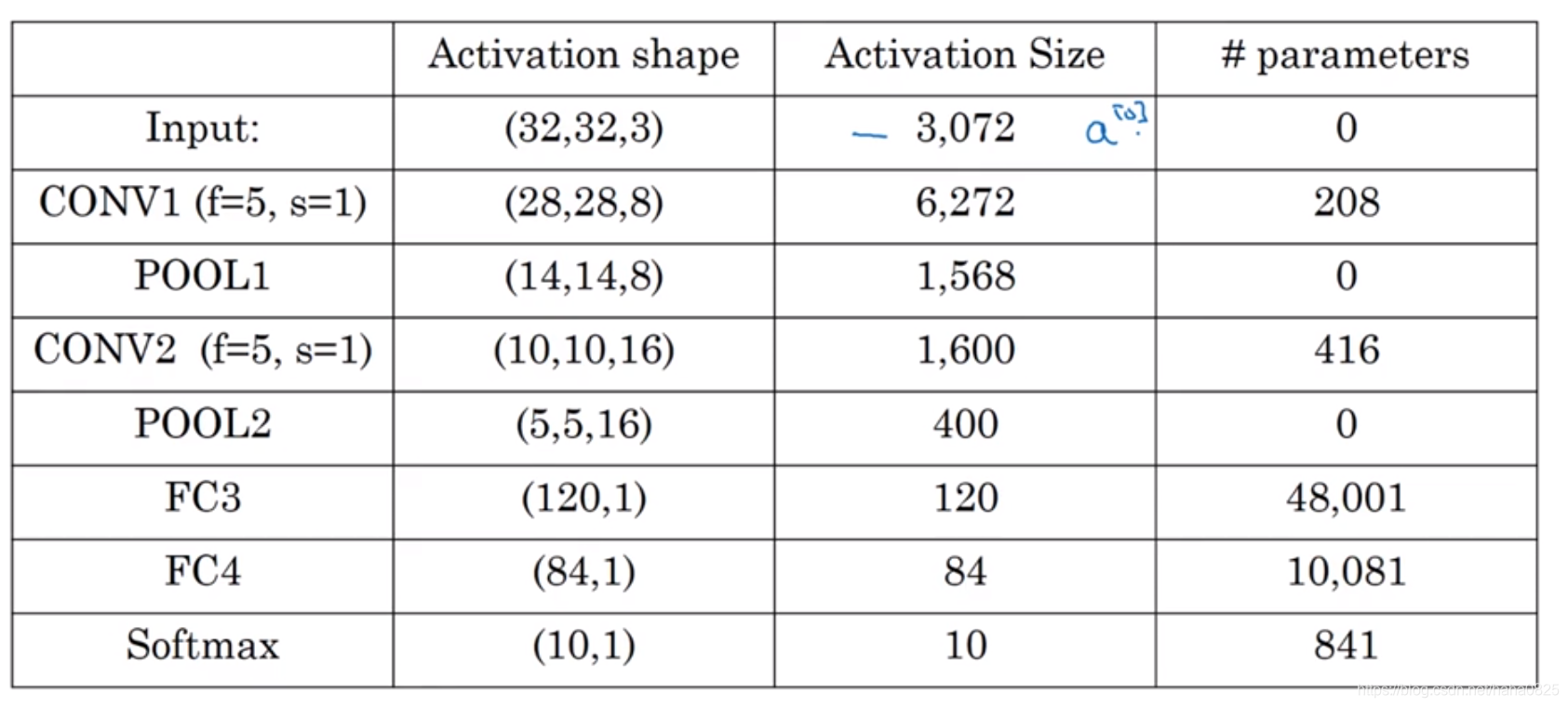
随着神经网络的加深，Activation Size会下降，如果下降得太快，会影响性能。

为什么使用卷积

与全使用全连接层相比，使用卷积有两个优点：

（1）参数共享：可以在输入图片的不同部分中使用相同的参数（过滤器），因此参数会少的多

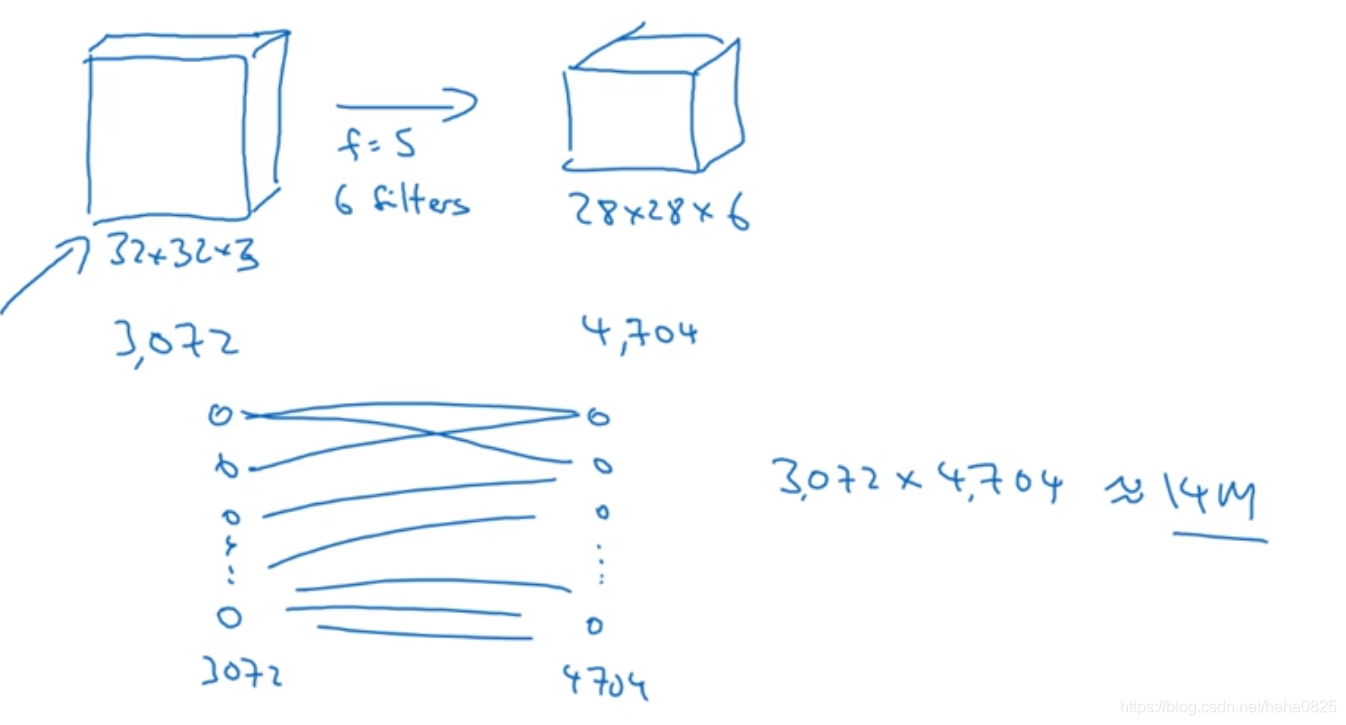
全部使用全连接层需要14万个参数，而使用卷积层只需要156个（（5*5+1）*6）。
（2）稀疏连接：在每一层，每个输出值仅由一小部分输入决定，而不是所有的输入决定，这样性能会好很多。

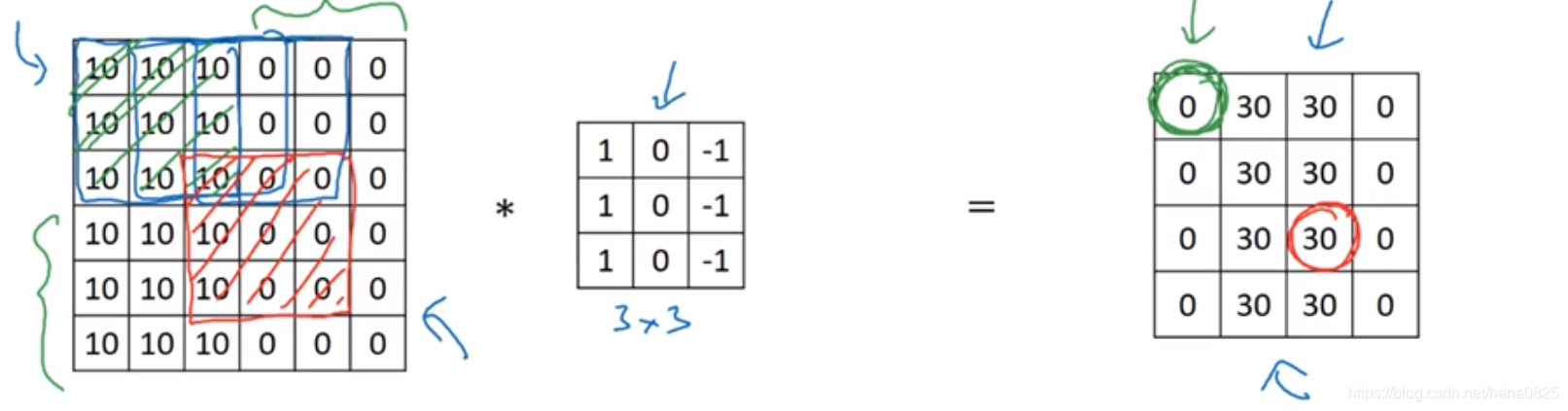
就如图中所示，输出的左上角的“0”只由输入的左上角那部分决定。

综合起来看

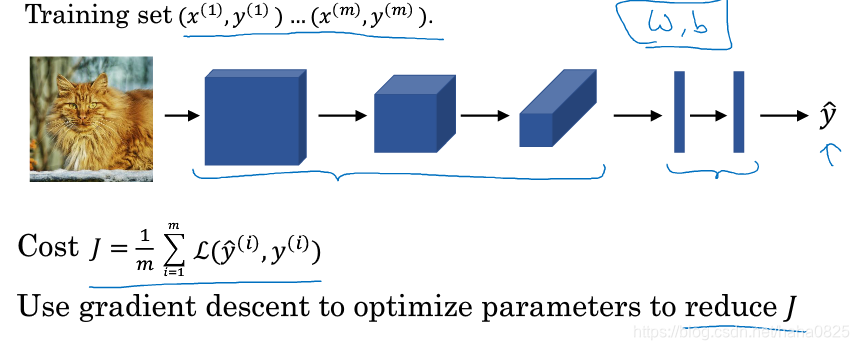
把输入层、卷积层、池化层和全连接层联系起来，最后再加上损失函数，然后使用梯度下降法来求得最优的结果，即损失函数值最小的参数。这就是一个完整的卷积神经网络。