题目: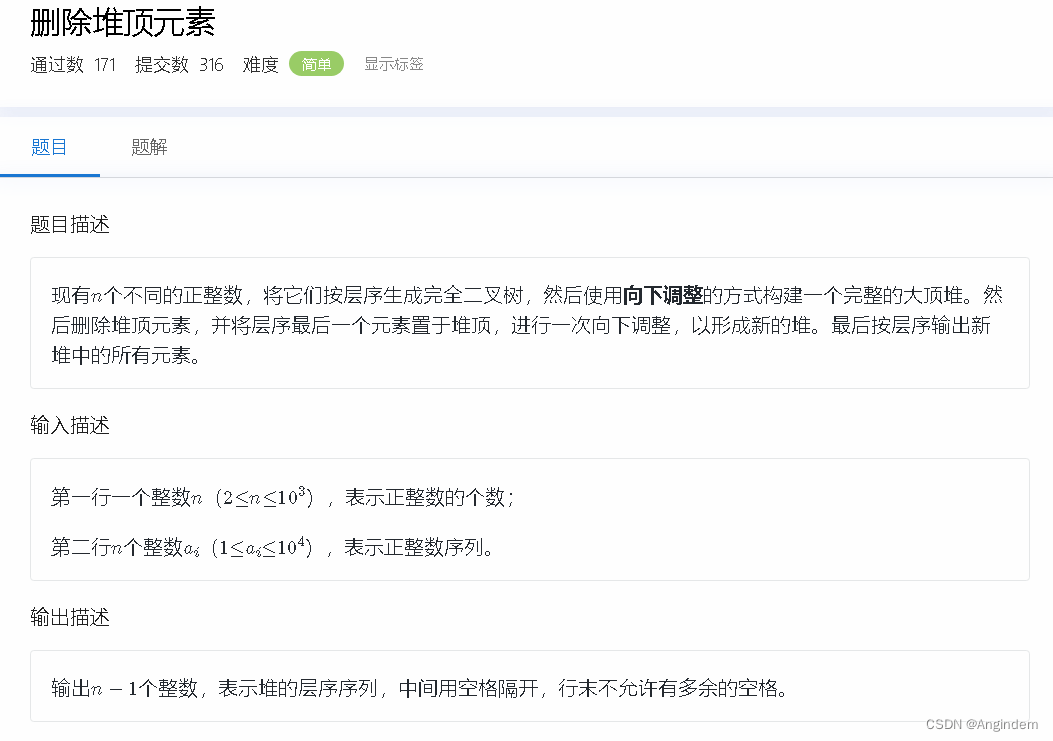
样例:
|
| 7 5 6 3 2 |
思路:
堆顶的删除,就是取 或者 覆盖掉 h[1],其中覆盖掉 h[1] 的操作,用向下调整操作堆即可,向下调整的过程相对简单,只需要将堆尾元素移动到堆顶,然后逐级与其较小(或较大)的子节点进行比较并交换位置。这个过程的时间复杂度是O(log n),其中n是堆中元素的数量。
即 h[1] = h[n--],downAdjust(1,n);
代码详解如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
umap<int,int>heap; // 建立堆数组
int n;
// 向下调整
inline void downAdjust(int low,int high)
{
int i = low,j = i << 1;
while(j <= high)
{
// 如果存在右孩子,并且右孩子 更符合 堆顶 性质,那么调整 右孩子
if(j + 1 <= high && heap[j + 1] > heap[j]) ++j;
// 堆调整
if(heap[j] > heap[i])
{
swap(heap[j] , heap[i]);
i = j;
j = i << 1;
}else break;
}
}
inline void DeleteTop()
{
heap[1] = heap[n--]; // 将尾堆 覆盖堆顶
downAdjust(1,n); // 向下调整堆
}
inline void solve()
{
cin >> n;
// 插入堆
for(int i = 1,x;i <= n;++i) cin >> heap[i];
// 根据题意,向下调整堆
for(int i = n / 2;i;--i) downAdjust(i,n);
// 删除堆顶元素
DeleteTop();
// 输出堆
for(int i = 1;i <= n;++i)
{
if(i > 1) cout << ' ';
cout << heap[i];
}
}
int main()
{
// freopen("a.txt", "r", stdin);
IOS;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}





 博客围绕堆顶删除算法展开,介绍了堆顶删除可通过取或覆盖 h[1] 实现,覆盖时将堆尾元素移到堆顶,再用向下调整操作堆,即逐级与较小(或较大)子节点比较交换,时间复杂度为 O(log n),还提及代码详解和最后提交。
博客围绕堆顶删除算法展开,介绍了堆顶删除可通过取或覆盖 h[1] 实现,覆盖时将堆尾元素移到堆顶,再用向下调整操作堆,即逐级与较小(或较大)子节点比较交换,时间复杂度为 O(log n),还提及代码详解和最后提交。


















 4729
4729

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








