八大排序之python

转载自：https://www.cnblogs.com/MrFiona/p/5978491.html
介绍之前先了解一下稳定与不稳定的概念：
在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。时间复杂度低，但时间不一定是最低的，由于忽略了维度低的量，但当n比较小时，维度低的可能反而比较大，大的量反而被忽略就容易导致复杂度低时间反而高的情况。

1. 冒泡排序：（稳定）
   换句话说也就是小的往上冒，大的往下沉。按照序列依次两两比较，重复进行，直到没有再需要交换。
   遍历方法：逐次遍历整个数列，把最小的放在最前面。
   代码如下：

def bubble_sort(a)
	for i in range(len(a)):
	    for j in range(i+1,len(a)):
	        if a[i] > a[j]:
	            a[i],a[j] = a[j],a[i]
	 return a

2.直接插入排序（稳定）
插入排序指的是插进已经排好的序列当中，将序列分为两部分，一部分是序列的前部分是排列好的，另外一部分需要一个一个的插入当中寻找合适的位置。
代码如下：

for i in range(1,len(a)):
    min1 = a[i]
    j = i-1 
    while j >= 0:
        if a[j] > min1:
            a[j+1] = a[j]
            a[j] = min1
        j -= 1

3.选择排序(不稳定）
基本算法是，第一趟每个数都跟第一个数相比较，如果比第一个数小，就交换位置，第二趟每个数都跟第二个数比较，如果比第二个小，就交换位置，依次类推。注意跟冒泡的区别，冒泡是依次两两比较把最小的放前，而选择是遍历后面，先把最小的位置选出来，再与前面交换。
代码如下：

for i in range(len(a)):
        min = i
        for j in range(i + 1, len(a)):
            if lists[min] > lists[j]:
                min = j
        a[min], a[i] = a[i], a[min]

4.快速排序（不稳定）
首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，然后再迭代这样一个过程。

def quick_sort(lists, left, right):
    if left >= right:
        return lists
    key = lists[left]
    low = left
    high = right
    while left < right:
        while left < right and lists[right] >= key:#left<right必须要加，以免减到负数
            right -= 1
        lists[left] = lists[right]
        while left < right and lists[left] <= key:
            left += 1
        lists[right] = lists[left]
    lists[right] = key
    quick_sort(lists, low, left - 1)
    quick_sort(lists, left + 1, high)
    return lists

5.希尔排序
插入排序的一种，不稳定，给序列分组，从大组再到小组，最后再逐个比较。
比如一个序列有八位list=[0,1,2,3,4,5,6,7],假设第一次分四组，那就是0-4,1-5,2-6,3-7他们相互比较，第二次分两组，就变成了 0246一组，1357一组 相互比较，最后分为一组依次比较
代码如下：

def shell_sort(slist):
    gap = len(slist)
    while gap > 1:
        gap = gap // 2
        for i in range(gap, len(slist)):
            for j in range(i % gap, i, gap):
                if slist[i] < slist[j]:
                    slist[i], slist[j] = slist[j], slist[i]
    return slist

6.堆排序
堆顶（小顶堆）的元素是整个堆中最小的元素，将堆顶元素与最后一个元素交换，然后用一次‘向下筛选’将新的堆顶元素移动到堆中正确的位置：即比较堆顶元素与其两个左右子结点的大小，如果堆顶元素最小，则将其保留在堆顶位置，停止；如果左子结点或右子结点最小，则交换堆顶元素与左子结点或右子结点的值，然后再沿着当前路径不断地比较下去，直至最初的堆顶元素在某一次比较中是最小值或者到达叶结点位置。

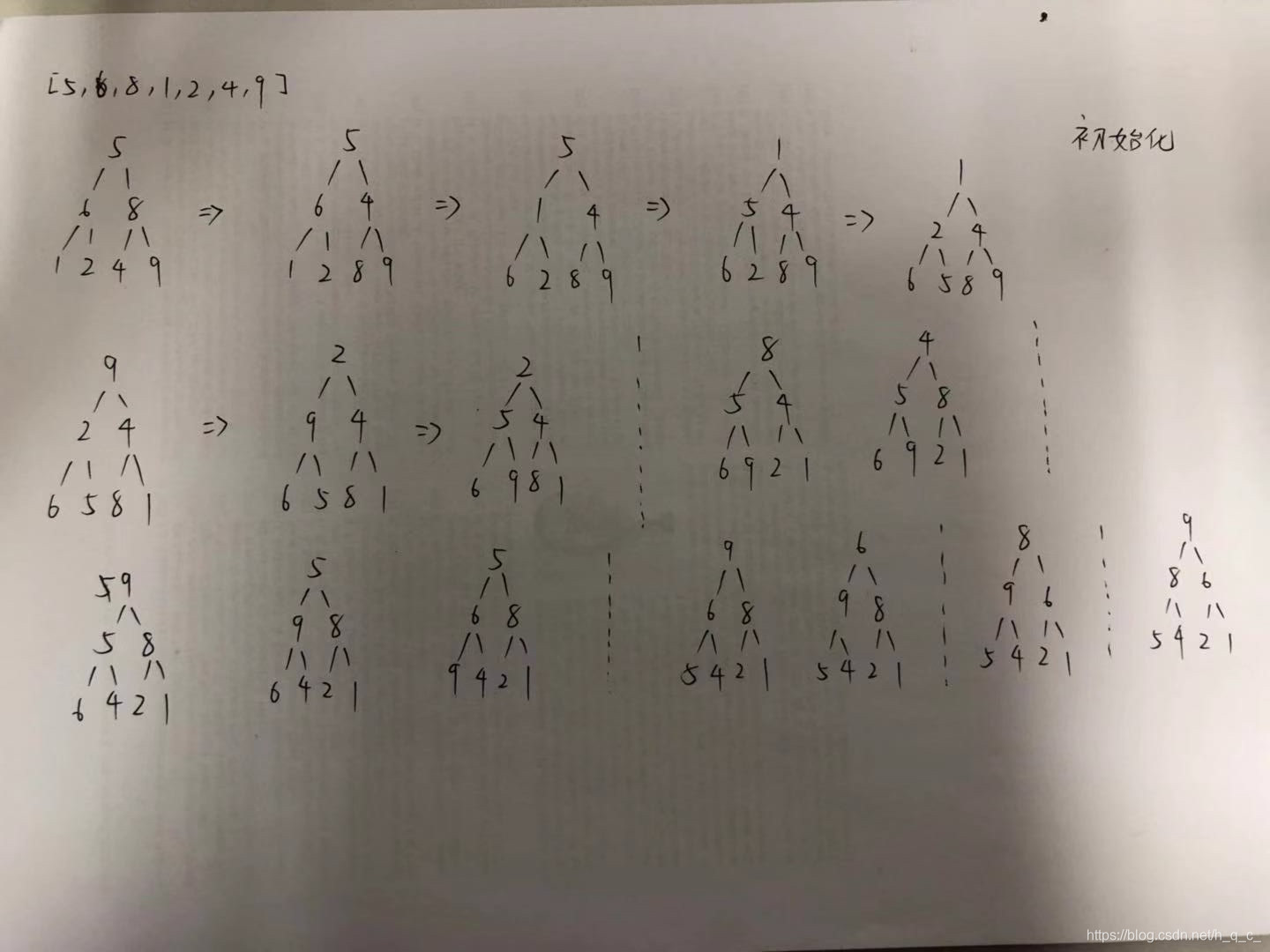
def heap_sort(elems):
    def siftdown(elems, e, begin, end): #向下筛选
        i, j = begin, begin*2+1 #j为i的右子结点，堆顶从0计数
        while j < end:
            if j+1 < end and elems[j] > elems[j+1]: #如果左子结点大于右子结点
                j += 1                              #则将j指向右子结点
            if e < elems[j]: #j已经指向两个子结点中较小的位置，
                break        #如果插入元素e小于j位置的值，则为3者中最小的
            elems[i] = elems[j] #能执行到这一步的话，说明j位置元素是三者中最小的，则将其上移到父结点位置
            i, j = j, j*2+1 #更新i为被上移为父结点的原来的j的位置，更新j为更新后i位置的右子结点
        elems[i] = e #如果e已经是某个子树3者中最小的元素，则将其赋给这个子树的父结点
                     #或者位置i已经更新到叶结点位置，则将e赋给这个叶结点。
        
    end = len(elems)
    for i in range(end//2-1, -1, -1): #构造堆序。
        siftdown(elems, elems[i], i, end)
    for i in range ((end-1), 0,-1): #进行堆排序.i最后一个值为1，不需要到0
        print(elems)
        e = elems[i] #将末尾元素赋给e
        elems[i] = elems[0] #交换堆顶与最后一个元素
        siftdown(elems, e, 0, i)
        

7.归并排序：
归并排序就是先拆分再合并的这样一个过程，不断地使用二分法，直至数组的长度等于1，然后逐个排序，然后逐步还原到原来的长度数组的这样一个过程。

def merge(left, right):
    #合并过程
    i, j = 0, 0
    result = []
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result

def merge_sort(lists):
    if len(lists) <= 1:
        return lists
    mid = len(lists) / 2
    left = merge_sort(lists[:mid])
    right = merge_sort(lists[mid:])
    return merge(left, right)

lst1 = raw_input().split()
lst = [int(i) for i in lst1]
#lst = input()
tt = merge_sort(lst)
for i in range(len(tt)):
    print tt[i],

八.基数排序
主要思想就是把数都放在桶中，假设都是两位数，个位数排一次序，然后再把十位数排一次序就好。如果三位以此类推。方法就是创建一个二维矩阵，要有10行，因为数字都是0-9的，把个位数按照大小匹配到对应的桶中去，排完之后读出来，再把十位的数按照大小匹配到对应的桶中。

import math
def radix_sort(lists, radix=10):
    k = int(math.ceil(math.log(max(lists), radix)))
    bucket = [[] for i in range(radix)]
    for i in range(1, k+1):
        for j in lists:
            bucket[j/(radix**(i-1)) % (radix**i)].append(j)
        del lists[:]
        for z in bucket:
            lists += z
            del z[:]
    return lists

lst1 = raw_input().split()
lst = [int(i) for i in lst1]
#lst = input()
radix_sort(lst)
for i in range(len(lst)):
    print lst[i]