从决策树到gbdt

1、决策树用做分类和回归

问题：

决策树如何做回归？

2、决策树的生成算法有哪几种

id3、c4.5、CART

3、决策树的结构：

内部节点表示特征，叶节点表示类。

决策树的内部节点的分支是多分支（一个内部节点可以有多个子节点）。

决策树每一层的特征（属性）都不相同。

4、决策树的特征选择：熵、条件熵、互信息、信息增益

决策树的特征选择的简单描述：如果一个特征具有更好的分类能力，那么依此特征将数据集分割成子集，使得子集在当前条件下有最好的分类，那么就应该选择这个特征，也就是说使用该特征划分子集后，各个子集内类别的不确定性更低（就是说各个子集内的样本几乎都属于1个类别）。

熵的公式：

条件熵的公式：，即X给定的条件下Y的条件概率分布的熵对X的的数学期望，即条件熵的均值。

信息增益就是互信息。

根据信息增益选择特征的方法是：对训练数据集D，计算每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。即给定条件下条件熵最小（也就是给定条件下类别纯度最高）。

在实际应用中，经验熵、经验条件熵、信息增益的计算方法：

给定数据集D，类别K，某个特征A：

经验熵：

经验条件熵：

信息增益：相减。

5、信息增益与信息增益比：

信息增益比的公式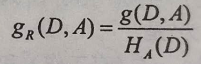：，其中是特征A的值的熵。

信息增益会倾向于选择特征的取值较多的特征，比如以物品的id为特征，一个物品对应一个id，则id3算法倾向于将每个数据自成一类，以id为特征的条件信息熵趋向于0，则信息增益最大，但是以id为特征没有意义，所以需要对其进行惩罚，惩罚系数就是以id为特征的情况下，id的个数为熵，将该熵作为分母，也就是说特征的取值个数越多，熵越大，对以该特征为条件得到的信息增益被惩罚的越厉害。

信息增益比也有缺点，倾向于特征取值较少的特征。

所以实际应用中，先用特征增益选取特征，然后再从其中使用信息增益比选取特征。

参考：https://www.zhihu.com/question/22928442/answer/117189907

6、ID3与C4.5的优缺点及区别:

参考：https://www.zhihu.com/question/27205203?sort=created

处理问题的目标相同：

C4.5和ID3都只能做分类。

样本数据差异：

ID3只能对离散变量进行处理，C4.5也可以处理连续变量（使用二分法，先对特征进行排序，然后取两个数的中间值为阈值进行二分切分）。

ID3对缺失值敏感，C4.5可以处理缺失值。

样本特征上的差异：

7、可以使用ID3或者C4.5进行特征选择。

8、决策树剪枝的原理及公式：

等号右边第一项意思是：生成的决策树，有T个叶子节点，每个叶子节点上可能有多个样本，并且可能属于不同的类别，如果一个叶子节点上的样本的类别比较单一，那么经验熵就会很小。

9、CART树是分类回归树，它假定决策树是二叉树

不同于ID3、C4.5算法的决策树，这俩算法得到决策树是多支的，而CART树是二叉的。

10、CART回归树的生成准则：

对于回归树用平方误差最小化准则，具体做法：

遍历所有的特征，在各个特征上寻找切分点，将样本划分为2个区域，寻找的切分点满足的条件是：两个区域内的样本的输出y的均值与该区域内所有的样本的标签之间的平方误差最小，之后在两个区域上重复上面的步骤。

11、这就表明一个问题：CART回归树在各个层上使用的特征是会有重复的，而ID3、C4.5生成的决策树在各个层上特征是不重复使用的。

12、也说明CART回归树的大致结构（输出结果，也即学习到的参数）就是：

每一层都会记录先挑选哪个特征，在每个内部节点也会有对该特征进行二分的切分阈值。

13、可以想象CART回归树的工作（预测）原理：

输入一个样本到决策树模型，模型的根节点会选中样本的某个特征索引，然后将该特征的特征值与模型记录的阈值进行比较，判断将样本划分到左分支还是右分支，然后在子树上重复上述步骤，直到叶子节点。

14、CART分类树的生成准则：

分类树用基尼指数选择最优特征及特征上的最优二值切分点。

15、基尼指数的定义

16、实际中怎么用基尼指数：

即：实际中用条件基尼指数，并且找条件基尼指数最小的特征及切分点。

17、adaboost的算法流程：

初始化训练数据的权值分布

基于已有的权值训练基本分类器

计算基本分类器在训练数据集上的分类误差率（分类误差率的公式）：

计算基本分类器的系数（系数计算公式）：

更新训练数据集的权值分布（更新公式，分子）

循环上面步骤，获得M个基本分类器及各个分类器对应的系数，将其组合到一起，获得最终分类器：

18、GBDT的推导公式：

gbdt与泰勒展开式

参考：https://blog.youkuaiyun.com/yangxudong/article/details/53872141

若损失函数是平方损失，则：

19、GB算法的框架：

推导：参考：https://www.bilibili.com/video/av24476653?from=search&seid=8683325314135471244

上图说明：

目标中的是我们已经学习到的树（或者其它模型），其中是输入到树中的样本，一般情况下求目标函数的值的时候是对中的参数求梯度使得与越来越接近，但是我们也可以把整个看成“参数”，直接对求梯度：，然后更新，其中，也就是梯度下降法中参数更新使用的学习率。

梯度提升的框架：

其中可以是树模型，也可以是其它模型（满足前向分步算法步骤）

20、gbdt中损失函数的种类：

参考：https://blog.youkuaiyun.com/qq_22238533/article/details/79185969

21、gb框架中，不同损失函数的初始模型的初值的计算方式：

22、gbdt中叶子节点的值的计算方式（依据损失函数的不同，有不同的计算方式）：

23、gbdt如何处理二分类：

参考：https://blog.youkuaiyun.com/qq_22238533/article/details/79192579

24、xgboost的初印象：

25、xgboost的可自定义损失函数的体现：

对损失函数用二阶Taylor展开近似。

26、泰勒展开与xgboost：

在第M步时：

损失函数：

参考泰勒展开式，则就是泰勒展开式中的x，而就是泰勒展开式中的，则的一阶导数就是：，二阶导数就是：。

那么损失函数用泰勒展开式来表示就是：

，又因为与，所以最终的损失函数可以表示为：

从这里可以看出xgboost只需要知道损失函数的形式，从而可以用梯度来表示损失函数。

27、xgboost中的树

参考：https://zhuanlan.zhihu.com/p/41207969

XGBoost的基学习器是CART回归树，但与李航的《统计学习方法》等教材里介绍的CART回归树不同，XGBoost使用的是模型树。简要的说，模型树的叶节点的输出值，不是分到该叶节点的所有样本点的均值（回归树），而是由一个函数生成的值。

树的定义：

这里W的长度就为3（叶子节点的个数）

树的复杂度：

28、xgboost完整的损失函数（二阶泰勒展开式+模型复杂度）：

29、xgboost中目标函数的求解方式：

前提是已经知道树的结构q，也就是样本属于叶子节点的索引，那么就对样本在该索引对应的叶子节点上的值w求导，另导数为零，就可以求出最佳w。注意：分数越小的树越好（分数就是损失函数的值）。

注意这里的前提是已知树的结构q，但是实际中树的结构q是通过贪婪方法，一个个试，通过比较每一种划分得到的分数，从而确定最终的q。

30、xgboost建树依据：

建树是对应于使得增益Gain最大的分裂点。

31、xgboost建树的方法：

精确搜索：

近似搜索：