机器人中液体晃动的SPH建模

机器人与自动化中液体晃动的建模

摘要

液体晃动是一种自由表面流动现象，在车辆、船舶或飞机的动力学（例如油箱中的晃动）、减振解决方案（例如调谐液体质量阻尼器）以及工业自动化和机器人系统（例如液体填充容器的处理）等应用中具有重要影响。无论晃动效应是被用来减少振动，还是相反地对系统引入干扰力，理解液体晃动动力学对于实现相应的期望系统行为都至关重要。为此，由于存在复杂的动力学效应，数值方法成为分析与优化的关键手段。在本研究中，我们聚焦于机器人技术与自动化背景下液体容器的运输与操作，并采用光滑粒子流体动力学（SPH）方法进行分析。通过文献实例对所选数值方法的特性与潜力进行了研究和评估，并提出了若干针对传统SPH实现的扩展，以提高精度和鲁棒性。

关键词 ：液体晃动，储罐晃动，晃动动力学，光滑粒子流体动力学，密度滤波，体积守恒

1. 引言

部分填充容器内流体的晃动运动在当今自动化工业过程的多个工程领域和具体应用中起着至关重要的作用（参见，例如，易卜拉欣等人（2001））。无论是车辆、航空或航天器油箱中的燃料晃动（参见，例如，图米等人（2009）），液体填充容器的自动化操作（矢野等人（2001），莫里埃洛等人（2018）），还是基于液态质量的振动阻尼器（参见，例如，高等人（1997）），这些情况均涉及复杂的自由表面流动与机械系统的耦合。液体晃动所产生的力可能对车辆或自动化系统的动力学与控制产生显著影响，可能导致机械强度与疲劳性能下降，但也可能被有益地利用。对液体晃动及耦合系统动力学的深入理解是实现成功系统设计的前提，且需针对具体应用设定优化目标。在自动化与机器人技术领域，当移动液体填充容器时，通常目标是在满足工艺时序、吞吐量或系统动力学约束的前提下，尽可能抑制晃动效应。本研究的动机正源于此——通过详细的离线及高效实时模型，支持此类系统的理解、设计、优化与控制。

尽管关于液体晃动动力学已有广泛的理论和解析成果（例如，参见易卜拉欣（2005）），但基于数值建模与仿真的方法在复杂系统设置、运动轨迹或容器几何形状的情况下能够提供更详细的见解。

已采用多种数值方法来模拟和研究晃动问题（参见，例如，雷布瓦亚和利克索诺夫（2010）），这些方法包括基于网格的方法，如使用水平集技术的两相流体有限元方法（巴塔利亚等人（2018））、采用流体体积法（VoF）技术的传统有限体积法（科诺普卡等人（2018））、混合基于网格的方法（陈塔内兹和穆勒（2011）），以及无网格技术，如光滑粒子流体动力学（SPH）（邵等人（2012），格林和佩罗（2018））或移动粒子半隐式方法（丰法赫（2016））。拉格朗日粒子方法相较于基于网格的方法的主要优势在于，自由表面流动和晃动效应——即使在复杂几何形状或运动情况下——能够被自然地捕捉，而无需显式追踪自由表面（例如，通过水平集技术、VOF方法或两相流建模）。

在本研究中，我们采用了粒子方法SPH，该方法已通过与柔性多体系统的耦合成功应用于多种流固耦合（FSI）问题（参见Schörgenhumer等人（2013）、舍尔根海默和胡默（2018）），而事实上，机器人与自动化系统中的液体晃动问题属于FSI问题的范畴。本文特别关注壁面边界条件的建模以及提高数值稳定性与一致性的技术。

本文的结构如下：在第2节中，描述了所采用的数值方法，包括已实现的扩展。在第3节中，将其应用于文献中的两个测试案例，以验证该方法、展示其潜力并进行研究。

2. 方法论

2.1 光滑粒子流体动力学（SPH）

无网格方法光滑粒子流体动力学（SPH）的主要原理是通过一组在非结构化但平均上均匀分布的粒子对连续介质进行离散。每个粒子被赋予一定的质量以及与具体问题相关的场变量，例如在热流体动力学中的速度、密度、压力和温度，或在固体力学中的应变和应力度量。问题域中任意一点$ \mathbf{r} $处的场变量$ f(\mathbf{r}) $首先通过积分形式的加权插值来近似

$$
f(\mathbf{r}) \approx \int f(\mathbf{r’}) W(|\mathbf{r}-\mathbf{r’}|, h) d^3\mathbf{r’}, \quad |\mathbf{r}-\mathbf{r’}| \leq 2h
\tag{1}
$$

在以点$ \mathbf{r} $为中心、半径为$ 2h $的球形域（即核支持域）上，其中$ h $表示所谓的光滑长度，$ W(|\mathbf{r}-\mathbf{r’}|, h) $为核函数。

在多种具有紧支集的核函数中，参见例如戈麦斯‐赫斯特拉（2010），采用五次多项式温德兰核（温德兰（1995））

$$
W(q,h) =
\begin{cases}
\frac{21}{256\pi h^3}(2 - q)^4(1 + 2q) & \text{for } q \in [0,2] \
0 & \text{otherwise}
\end{cases}
\quad \text{with } q = |\mathbf{r}-\mathbf{r’}|/h
\tag{2}
$$

是一种流行的选择，也在本研究中被采用。(1) 的SPH离散化由所谓的粒子近似给出

$$
f(\mathbf{r}) \approx \sum_j f_j \frac{m_j}{\rho_j} W(|\mathbf{r}-\mathbf{r}_j|, h), \quad |\mathbf{r}-\mathbf{r}_j| \leq 2h
\tag{3}
$$

对位于$ \mathbf{r} $周围平滑域内的所有粒子求和，其中$ f_j $是与粒子$ j $相关的场变量$ f $的值，$ m_j $和$ \rho_j $分别为其质量和密度。在三维问题中，光滑长度$ h $通常选为$ [\Delta x, 1.5\Delta x] $范围内，其中$ \Delta x $表示平均粒子间距，使得平滑域内大约包含40–100个粒子。

基于无结构插值（3），将所考虑问题的控制方程离散化，得到一组关于粒子的位置和速度$ \mathbf{r}_i $和$ \mathbf{v}_i $的常微分方程——即运动方程，以及关于场变量随时间变化的方程。质量和相关物理量随着粒子移动，如同物质点一样，这使得光滑粒子流体动力学成为一种无网格拉格朗日方法。

该方法最初源于天体物理问题中的气体动力学背景（参见，例如，卢西（1977）），随后由莫纳汉（1994）将其应用于自由表面流动。多年来，它已成功应用于固体力学与流体力学的各类问题，例如参见Monaghan (2005)或Liu and Liu (2010)。由于其无网格拉格朗日特性，光滑粒子流体动力学特别适用于涉及自由表面和随时间变化区域的复杂流动问题（如流固耦合（舍尔根海默等人（2013））或流动与混合在部分填充的复杂几何结构（Eitzlmayr 和 Khinast (2015)），因为它既不需要显式追踪自由表面，也不需要采用网格自适应或插值技术来处理随时间变化的区域。

为了研究本研究中的晃动问题，我们将弱可压缩等温牛顿流体的纳维‐斯托克斯方程采用SPH离散格式(3)进行离散化。每个粒子$ i $的运动方程以对称形式表示（以增强一致性）

$$
\dot{\mathbf{r}}_i = \mathbf{v}_i
$$

$$
\dot{\mathbf{v}} i = -\sum {j,|\mathbf{r} {ij}|<2h} m_j \left( \frac{p_i}{\rho_i^2} + \frac{p_j}{\rho_j^2} \right) \nabla_i W(\mathbf{r} {ij}, h) + \frac{2\eta}{\rho_i} \sum_{j,|\mathbf{r} {ij}|<2h} m_j \frac{\mathbf{v} {ij} \cdot \mathbf{r} {ij}}{|\mathbf{r} {ij}|^2} \nabla_i W(\mathbf{r}_{ij}, h) + \mathbf{g}
\tag{4}
$$

其中$ \mathbf{r} i $、$ \mathbf{v}_i $、$ p_i $、$ \rho_i $分别表示粒子的位置、速度、压力和密度，$ \eta $为动力粘度，$ \mathbf{g} $为重力，以及$ \mathbf{r} {ij} = |\mathbf{r} i - \mathbf{r}_j| $和$ \mathbf{v} {ij} = \mathbf{v}_i - \mathbf{v}_j $。粘性项根据莫里斯等人（1997）进行建模。密度由连续性方程计算得出。

$$
\dot{\rho} i = \sum {j,|\mathbf{r} {ij}|<2h} m_j \mathbf{v} {ij} \cdot \nabla_i W(\mathbf{r}_{ij}, h)
\tag{5}
$$

压力通过所谓的泰特状态方程与密度相关（参见莫纳汉（1994））

$$
p_i(\rho_i) = \frac{c_0^2 \rho_0}{\gamma} \left[ \left( \frac{\rho_i}{\rho_0} \right)^\gamma - 1 \right]
\tag{6}
$$

其中$ \rho_0 $表示参考密度，$ c_0 $表示声速，常数$ \gamma $通常取值为7。有关(4)–(6)推导的更多细节，可参见Monaghan (2005)或Liu and Liu (2010)。

以下两个关键方面补充了上述经典SPH公式，将在接下来的小节中进行说明，并在本研究中更详细地探讨：壁面边界条件的建模，以及密度场的平滑与修正技术，以消除虚假噪声并保持稳定性与一致性。

2.2 壁面相互作用模型

如果流体与固体壁面接触，则在界面的每个点上都需要满足两个局部边界条件，即所谓的无滑移条件。

$$
\mathbf{v} {solid} = \mathbf{v} {fluid}
\tag{7}
$$

以及力的平衡，

$$
\boldsymbol{\sigma} {solid} = \boldsymbol{\sigma} {fluid}
\tag{8}
$$

使用固体和流体区域的局部速度$ \mathbf{v} {solid} $、$ \mathbf{v} {fluid} $和应力张量$ \boldsymbol{\sigma} {solid} $、$ \boldsymbol{\sigma} {fluid} $。已有多种不同的方法被提出用于在光滑粒子流体动力学中实施壁面边界条件，详细综述可参见舍尔根海默（2016）。在本研究中，我们采用并比较以下两种方法。

首先，下文将简称为(SPH) 壁面模型A的力场方法进行考虑，其中在光滑粒子流体动力学情况下当粒子足够接近（通常在范围内）边界时，会产生排斥和粘性罚力

$$
\mathbf{f} {rep} = \int \boldsymbol{\sigma}_r d\Gamma \quad \text{and} \quad \mathbf{f} {visc} = \int \boldsymbol{\sigma}_v d\Gamma
\tag{9}
$$

在局部壁面单元与SPH粒子之间计算并施加相互作用力，以近似边界条件（7）和（8）。在公式（9）中，$ \boldsymbol{\sigma} r $和$ \boldsymbol{\sigma}_v $分别为排斥力和粘性力的短程表面密度，$ \Gamma $为流体‐固体界面，$ \mathbf{r} {wall} $和$ \mathbf{v}_{wall} $分别表示SPH粒子与$ \Gamma $上局部积分点之间的相对位置和速度。公式（9）中的面卷积积分基于通过三角形STL网格离散化的边界$ \Gamma $，采用高斯‐勒让德求积进行数值计算。更多细节参见舍尔根海默等人（2013）。

第二种方法，下文称为(SPH) 壁面模型B，利用了壁面边界粒子的概念，但并不实际引入额外的粒子，而是通过多项式拟合其缺失的贡献，并将这些贡献添加到壁面附近的粒子的控制方程（4）和（5）中（艾茨尔迈尔等人（2014））。添加到动量方程（4）中的项具有如下形式

$$
\dot{\mathbf{v}} {\Gamma} = -\frac{m_i}{\rho_i^2 h^4} F {\nabla W} \mathbf{n} {\perp} - \frac{m_i 2\eta \mathbf{v} {i,wall,\parallel}}{\rho_i^2 h^5 (1 + \Delta x / 2r_{i,wall,\perp})} F_{\nabla W/r}
\tag{10}
$$

对于连续性方程，我们有

$$
\dot{\rho} {\Gamma} = \frac{m_i \mathbf{v} {i,wall,\perp}}{h^4} F_{\nabla W}
\tag{11}
$$

其中$ \mathbf{n} {\perp} $表示壁面法向方向，定义为从光滑粒子流体动力学粒子指向壁面边界上最近点的单位向量$ \Gamma $, $ \mathbf{v} {i,wall} $表示粒子相对于壁面的速度，$ \mathbf{v} {i,wall,\perp} $为$ \mathbf{v} {i,wall} $在$ \mathbf{n} {\perp} $方向上的分量，$ r {i,wall,\perp} $为粒子到壁面的最短距离。因子$ F_{\nabla W} $和$ F_{\nabla W/r} $包含作为距离函数的边界粒子贡献的四阶多项式拟合$ r_{i,wall,\perp} $。

方程(10)和(11)用于补偿位于距离壁面$ 2h $范围内的粒子的核支持域被截断的问题，这种截断由于缺少邻近粒子而导致求和式(3)不完整且不一致。为了确保粒子不穿透壁面，引入了一种额外的短程排斥力，该力沿SPH粒子与最近的壁面单元之间的$ \mathbf{n}_{\perp} $方向作用。复杂边界几何形状再次由三维三角形曲面网格表示。

两种壁面模型均通过第3节所述的数值算例进行了测试和比较。

2.3 密度场的平滑与修正

在弱可压缩SPH公式中，对密度场进行适当的平滑（通常在10–50个时间步长的间隔内）对于抑制虚假噪声并保持数值稳定性至关重要。在本研究中，我们采用了一阶一致移动最小二乘（MLS）滤波器，其中粒子$ i $的平滑密度值$ \rho_i^* $通过求解线性方程组得到。

$$
\mathbf{M} \cdot (\rho_i^ , \frac{\partial \rho_i^ }{\partial x}, \frac{\partial \rho_i^ }{\partial y}, \frac{\partial \rho_i^ }{\partial z})^T = \mathbf{b}
$$

$$
\mathbf{b} = -\sum_{j,|\mathbf{r} {ij}|<2h} \frac{m_j}{\rho_j} W {ij} (-1, x_{ij}, y_{ij}, z_{ij})^T
$$

$$
\mathbf{M} = \sum_{j,|\mathbf{r} {ij}|<2h} \frac{m_j}{\rho_j} W {ij}
\begin{pmatrix}
1 & -x_{ij} & -y_{ij} & -z_{ij} \
& x_{ij}^2 & x_{ij}y_{ij} & x_{ij}z_{ij} \
& & y_{ij}^2 & y_{ij}z_{ij} \
& & & z_{ij}^2
\end{pmatrix}
\tag{12}
$$

使用$ (x_{ij}, y_{ij}, z_{ij})^T = \mathbf{r} i - \mathbf{r}_j $和$ W {ij} = W(\mathbf{r} {ij}, h) $。关于MLS方程的推导，参见例如戈麦斯‐赫斯特拉（2010）。在每一次平滑步骤中，求解线性方程组(12)，并将$ \rho_i $替换为$ \rho_i^ $。上述MLS滤波器是一阶一致的，即能够精确复现并因此守恒线性密度或压力场——或恒定梯度——与之相比，著名的谢泼德滤波器（参见例如Gomez‐Gesteira（2010））仅为零阶一致，会逐渐消除所有类型的梯度。只有当出现病态系统(12)时（这种情况可能发生在粒子孤立或在其平滑域内仅有极少邻居的情况下），才将$ \rho_i^ $替换为相应的谢泼德插值$ b_1/M {11} $（下标索引表示对应的分量）。

本研究中采用的SPH公式的第二个重要扩展是对密度场进行校正，以保持流体的体积，即SPH粒子占据的区域。需要注意的是，无论是连续性方程(5)的积分，还是上述密度滤波器，均未严格建立SPH粒子占据的区域、相应的质量分布与密度场之间的一致关系。这一缺陷也由伊菲尔等 (2017) 报道过，他们提出了一种密度校正方法，以保持用恒定体积完全填充封闭隔室，该方法通过周期性、均匀的密度场偏移实现，即不改变梯度。然而，对于自由表面流动，需要对该技术进行扩展。密度求和，即通过$ \rho_i $计算

$$
\rho_i^{sum} = \sum_{j,|\mathbf{r} {ij}|<2h} \frac{m_j}{\rho_j} W(\mathbf{r} {ij}, h)
\tag{13}
$$

而不是(5)，这将在空间质量分布与密度场之间建立一致关系（参见舍尔根海默（2016）），但由于粒子分布不均以及在区域边界附近存在缺失贡献的问题，该方法并不可行。尽管在本研究中我们仍使用(5)来计算密度场，但我们利用(13)的性质，并提出以下针对体积守恒的修正方法：在每次应用MLS密度滤波后，计算所有N个粒子的平均求和密度以及平均实际密度，

$$
\rho_{avg}^{sum} = \frac{1}{N} \sum_{i=1}^N \rho_i^{sum} \quad \text{and} \quad \rho_{avg} = \frac{1}{N} \sum_{i=1}^N \rho_i
\tag{14}
$$

随后，密度场被调整为校正值，类似于伊菲尔等 (2017) 的方法。

$$
\rho_i^{corr} = \rho_i + (\rho_{avg}^{sum} - \rho_{avg})
\tag{15}
$$
根据(15)调整密度场显著增强了体积守恒，同时保留了密度和压力梯度，并且由于边界或自由表面附近不一致性（如上所述，源于密度求和方法(13)）导致的误差较小。适当的密度平滑以及所提出的体积守恒扩展的性质和重要性将在下一节的测试案例中予以验证。

3. 结果与讨论

该方法已应用于近期文献中的多个实例，这些实例同时提供了测量数据以及解析和数值模型的结果。第2节中描述的SPH公式已在粒子模拟程序LIGGGHTS（参见 CFDEM (2019)）中实现，并与用于机电一体化与多物理场问题的模拟工具HOTINT耦合（参见Gerstmayr 等人 (2013)，HOTINT (2019)），以执行晃动问题的耦合仿真与分析。

3.1 测试用例1 – 莫里埃洛等人（2018）

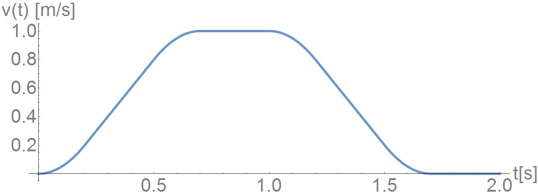
在第一个示例中，考虑了一种液体处理机器人系统。莫里埃洛等人（2018）原始研究的目标是抑制液体填充容器在点对点运动中的晃动。为此，控制策略采用了简化解析摆模型，并对一阶晃动模态的频率和阻尼（取决于容器的填充水平）以及给定轨迹下的晃动动力学进行了测量。实验中，使用半径为97.5毫米的圆柱形容器，分别装入1、2和3升水（动力粘度接近1毫帕·秒），并定义了沿地面平行直线的轨迹，其速度曲线如图1所示。

所提出的数值方法已应用于该用例——为说明起见，请参见图2中的仿真快照——并研究了壁面模型、密度平滑及修正、空间分辨率和平滑离散化（由比率$ h/\Delta x $确定）的影响。

默认的SPH设置中，我们使用了Wendland核函数 (2)、相对粗略的空间分辨率（1升水对应≈15000个粒子）以及$ h/\Delta x= 1.25 $（导致核支持域内有≈65个粒子），并结合MLS滤波器 (12) 和密度修正 (15)，每40个时间步长进行一次。对于状态方程 (6)，参数选择为$ \rho_0=1000 $ kg/m³、$ \gamma= 7 $和$ c_0= 3 $ m/s，使得密度变化保持在百分之几以内（另见莫纳汉（1994））。

首先，针对两种SPH壁面模型以及两种不同的$ h/\Delta x $比值（$ \Delta x $保持为常数）对容器上的晃荡力进行了比较。所有其他设置均相同，并按上述方式选定。需要注意的是，简化解析模型（如莫里埃洛等人（2018）中的摆动模型）通常无法在未经测量或高分辨率数值模拟模型标定的情况下提供准确的力。

：壁面模型B，$ h/\Delta x= 1.25 $。红线 (b)：壁面模型A，$ h/\Delta x= 1.25 $。蓝线 (c)：壁面模型A，$ h/\Delta x= 1.0 $)

如图3所示，尽管在所有三种情况下，主导晃动模态的频率以及容器初始运动阶段的力都能得到相对准确的预测，但数值阻尼却显著依赖于模型设置。我们观察到，壁面模型B（见图3中的曲线(a)）通常比壁面模型A（图3中的曲线(b)和(c)）引入的阻尼明显更小，但在所产生的力中伴随有更大的噪声。这可以通过壁面模型A在边界附近引入的不一致性来解释。尽管惩罚力(9)近似满足条件(7)和(8)，排斥力和粘性项却与SPH公式不一致，并且对密度（和压力）场没有贡献，从而导致诸如靠近壁面处出现过密的粒子层等伪影。当一个SPH粒子接近固体边界时，排斥力可防止穿透并建立力的平衡，然而由于墙另一侧的邻近粒子缺失，该粒子的密度和压力缺乏相应的贡献，这与壁面模型B的特性不同。我们认为，这些不一致性结合粘性惩罚项会导致过度耗散。另一方面，在力的平滑性方面，壁面模型B不仅直接耦合了粒子位置，还将压力值与壁面相互作用相耦合，这往往会产生更多的噪声。

与壁面模型A的积分惩罚项相比，通过增加$ h $来提高比率$ h/\Delta x $——这会增加式(1)中的平滑误差，但由于核支持域内粒子数量增多，相对于式(1)降低了式(3)的离散化误差——显著减小了阻尼效应（参见图3中曲线(b)与(c)的对比）。这种效应主要出现在壁面模型A中，而模型B的结果几乎不受$ h/\Delta x $的影响。其原因目前尚不明确。需要注意的是，在所有情况下，流体均采用了相同的粘度模型和参数，即使耗散最小的情况也显示出比实验结果更高的数值阻尼。对复杂耗散过程的更深入分析将是未来工作的重点。最近已有研究涉及耗散问题及长时间稳定性问题，例如格林和佩罗（2018）在储罐晃动背景下的研究。

接下来，研究了主导晃动模态的频率随壁面模型、空间分辨率（$ \Delta x $）以及平滑域大小（$ h $）的变化情况。充装量为1升时的结果汇总于表中。即使在相对粗糙的分辨率下（粒子数量较少），尤其是使用壁面模型B时，仍获得了与测量结果较为一致的结论，其与实验参考值$ f_{exp}= 1.65 $ Hz的偏差仅为百分之几。对于更高的充装量，也得到了类似的结果。

$ \Delta x $	粒子数	$ h/\Delta x $	$ f_A / f_{exp} $	$ f_B / f_{exp} $
3	37037	1.25	0.934	0.981
4	15625	1.25	0.915	0.979
5	8000	1.25	0.908	0.966
4	15625	1.0	0.969	0.995
4	15625	1.5	0.888	0.973

壁面模型A通常产生较小的频率，这是由于其数值阻尼明显高于壁面模型B，参见前述讨论以及图3。如预期所示，随着空间分辨率的提高（即$ \Delta x $更小），结果向实验结果收敛。相反，增大比率$ h/\Delta x $会导致（略微）更小的频率，同时阻尼降低。该发现有待进一步研究。

最后，针对长时间模拟中的密度场平滑性和一致性进行了研究，示意图见图4。一阶一致MLS滤波器（12）与体积修正（15）相结合，产生了理想的行为，即得到了一致的密度场和压力场（参见图4(a)中的线性静水压力分布），同时实现了体积守恒。而（零阶一致的）谢泼德滤波器如预期般逐渐导致压力场和体积出现不一致（参见图4(b)），即使采用了（15）。若省略体积守恒的修正（15），则无法获得长期稳定结果（图4(c)）。综上所述，对于密度场而言，一致的平滑与修正技术对于获得满意的结果至关重要，尤其是在长时间模拟中。一种替代本文所述方法的选择是所谓的δ-SPH方案，更多阅读请参见格林和佩罗（2018）。

带修正（15）的MLS滤波器(12)、(b) 带修正的谢泼德滤波器，以及 (c) 不带修正的MLS滤波器，在60秒模拟时间后容器静止时的稳态解。红线表示目标填充高度。底部的静水目标压力约为330 牛/平方米)

3.2 测试案例 2 – 巴塔利亚等人（2018）

在第二个示例中，研究了矩形罐在谐波激励下稳态晃动的波幅频率响应。有关实验设置的详细信息，请参见巴塔利亚等人（2018）。图5展示了两种SPH壁面模型的结果与测量值的对比。研究结果与前一个示例一致——两种壁面模型均得到令人满意的结果，其中模型B与实验参考值非常接近，而模型A由于具有更高的数值阻尼，导致波高和频率较小。

4. 结论

提出的用于晃动问题的基于模型的分析的数值方法已显示出良好的结果。关于基础SPH公式，固体壁面边界条件的建模以及密度场的一致性处理已被证明至关重要。一些特定方面，特别是壁面附近的稳定性、平滑性和一致性，以及数值耗散，仍有待进一步研究。

目前，一个包含摄像头和力传感器的自动化试验台正在建设中，用于对液体填充容器中的晃动进行详细的实验分析。测量还应用于仿真模型的标定和验证。这些研究活动的未来目标是基于精细数值仿真和实验数据，开发并标定可在实时运行的简化模型，并研究其适用性和潜力，最终目的是在自动化领域的软硬件框架中实现这些简化模型的应用，参见泽特莱特纳等 (2019)。