GAMES101---学习笔记--自用--3D transformations

一、 3D transformations

1. 基本原理

(x, y, z, w) (w != 0) 其实是3维空间中的点 (x/w, y/w, z/w），用齐次坐标来表示三维的点和向量，与二维同理。

  对于4*4仿射变换（即线性变换+平移）。三维空间中的顺序仍然是先线性变换再做平移。

2. 三维变换

下面是它的缩放和平移的公式：

  缩放时变换的为$ s_{x}、s_{y}、s_{z} $，三个轴缩放的变化可以各不相同，3\ast 3的对角阵。平移是最后一列$ t_{x}、t_{y}、t_{z} $在变化，实现三个轴方向的平移。

  任意的旋转写出来难度很大，我们来看一个物体绕着三个轴的旋转。从图中绕着X轴旋转时，我们可以发现这个物体的Y、Z坐标的点是在旋转的，而X的点没有变化。

  Y轴旋转时，根据右手螺旋定则，思考这些轴的顺序，$ x×y=z、y×z=x、 $可以看出循环对称的性质，即$ z×x=y $ 是反的。

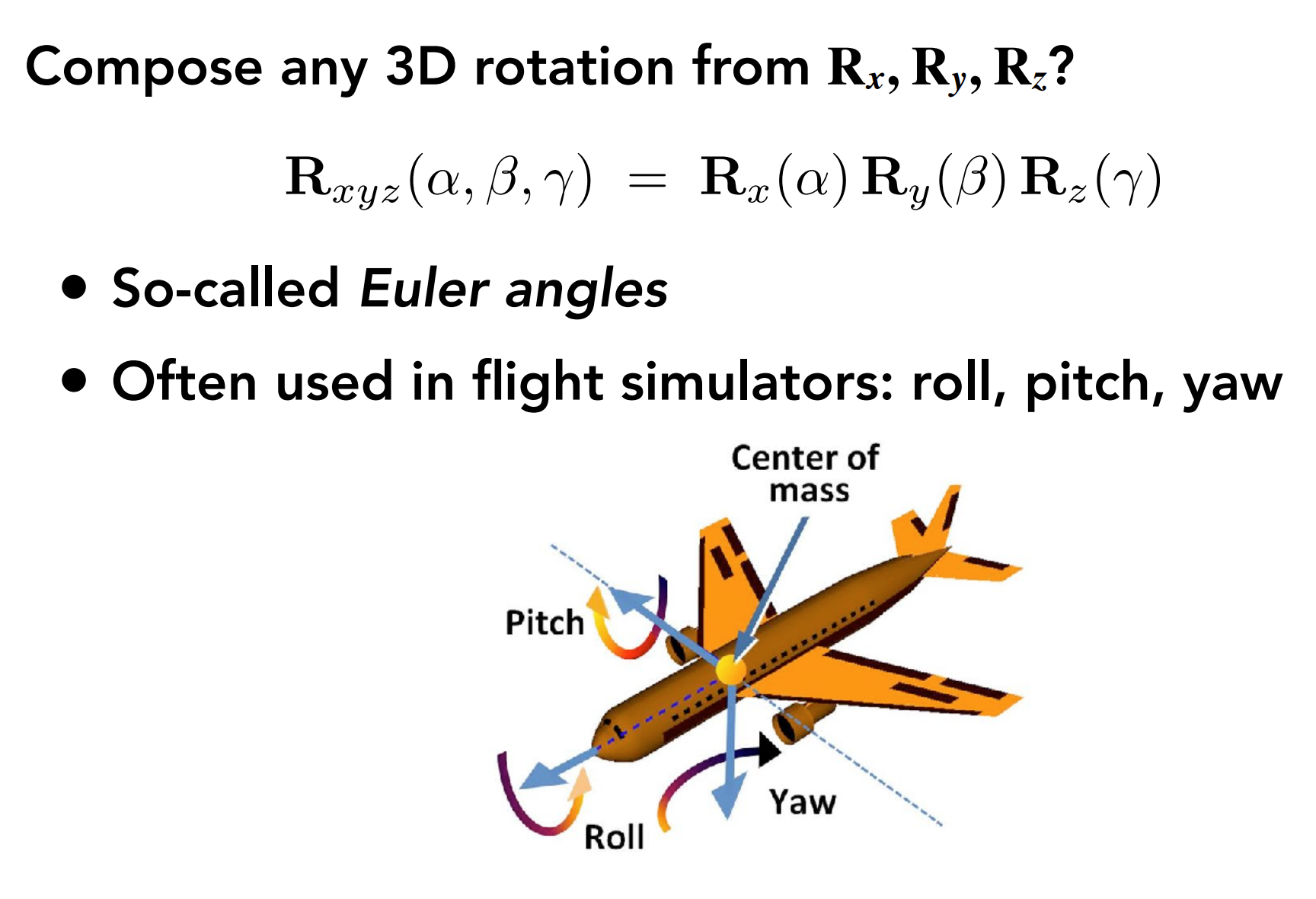
   任意一个旋转都可以被分解成由绕x，y，z轴的三个旋转合成的一个旋转，就是所说的欧拉角（Euler angle）,因此计算机图形学领域中有人提出了Rodrigues’ Rotation Formula(罗德里格斯旋转公式)。

$\mathbf{R}(\mathbf{n},\alpha )=\cos (\alpha )\mathbf{I}+(1-\cos (\alpha ))\mathbf{n}{\mathbf{n}}^T+\sin (\alpha )\underset{\mathbf{N}}{\underbrace{\left(\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right)}}$

   注意这个旋转轴n用向量表示，就是该向量过原点产生的射线。如果我们想让物体沿任意轴旋转(包括不过原点的轴)，可以和二维图像围绕任一点旋转一样，先平移到过原点轴进行旋转，再平移回去。具体推导如下所示：

二、Viewing (观测) transformation

1. View (视图) / Camera transformation

  我们可以这样来描述视图变换的任务：将虚拟世界中以（x,y,z)为坐标的物体变换到 以一个个像素位置(x,y) 来表示的屏幕坐标系之中(2维)，这确实是一个较为复杂的过程，但是整个过程可以被细分为如下几个步骤：

(1) 模型变换(modeling tranformation)：这一步的目的是将虚拟世界中或者更具体点，游戏场景中的物体调整至他们应该在的位置。

(2) 摄像机变换(camera/view tranformation)：在游戏中我们真正在乎的是摄像机(或者说眼睛)所看到的东西，也就是需要得到物体与摄像机的相对位置（角度）。

(3) 投影变换(projection tranformation)：根据摄像机变换得到了所有可视范围内的物体对于摄像机的相对位置坐标(x,y,z)之后，便是根据是平行投影还是透视投影，将三维空间投影至标准二维平面([-1,1]^2)之上 （tips：这里的z并没有丢掉，为了之后的遮挡关系检测）。

(4) 视口变换(viewport transformation)：将处于标准平面映射到屏幕分辨率范围之内，即[-1,1]^2→ \rightarrow→[0,width]*[0,height], 其中width和height指屏幕分辨率大小。

1.1如何定义初始的观测矩阵

                                                          相机的位置->往哪看->向上方向

1.2 Key observation

   如果摄像机和场景中所有的东西一起移动的话，那么整个场景在摄像机中的画面还是相对保持不变。

  我们假设永远都是物体在运动而相机是没有动的，并且相机永远放在三维坐标系的原点，永远向$ -z $的方向在看，向上的方向为Y轴。这时再根据上述的定义将物体随着相机运动，并将相机运动到原点，可以简化处理。

具体的变化方法如下：

相机和物体初始位置

变换以后的位置

  如何写成矩阵形式：$ M_{v i e w}=R_{v i e w} T_{v i e w} $这个是最重要的。我们知道一个矩阵的时候是先做线性变换再做平移，而变换相机位置时，我们先平移其位置再做旋转。

旋转时：中心思想就是我们先反过来写，在给他变回来。

即旋转矩阵的逆就是它的正交矩阵，我们直接求它的转置就可以。

总结:

1、任何时候只要是相机和物体都应用同样的变换，移动方法，只要相机移动到规定的位置上，即物体也就变化到需要的位置上。

2、视图变换操作的是相机，物体随着变换。

2. Projection transformation （投影变换）

2.1投影方式

正交投影：正方体，不会有近大远小的特点

透视投影：椎体，无限延长的平行线好像相交，近大远小

2.2 正交投影

   对于正交投影，最简单的理解方式就是将所有三维空间的物体挤压到一个二维的平面，也就是将所有物体的z坐标直接去掉，最后将图形压缩到[-1,1]的二维区域内。也就实现了从三维到二维平面的映射。

实际操作：

  即我们将空间中的一个长方体映射成标准的正方体。先做平移在做缩放，在Z轴上定义远和近，越近Z值越大，越远Z值越小，沿着-Z的方向看（右手系）。具体矩阵变换方式：

  先通过一个位移矩阵将长方体中心移动到原点，再通过一个缩放矩阵将长方体压缩成一个立方体。

2.3 投影矩阵

实现方式：

  齐次变换后的点表示都是同一个点，比如（1，0，0，1）和（2，0，0，2）表示的都是（1，0，0）点。

  我们要通过变换将左侧这个视锥“挤”成右边这个长方体，再做一次正交投影，问题就解决了。在上面我们已经知道正交投影怎么做了，所以现在所有的问题集中在如何将这个视锥“挤”成右边这个长方体。（即将透视投影的锥体变换成长方体）

  在此我们定义几个问题。首先近平面在挤压之后，任何一个点都不会变，远平面在挤压过程中，Z值不会变，也就是说挤压之后远平面的Z值依然是f；远平面的中心点在挤压之后也不会发生变化，x、y依然是0，z=f。

保证以上条件的实现，接下来我们看看怎么将左侧这个视锥“挤”成右边这个长方体：

  通过侧视图，对于视锥上任意一个点（x，y，z）和近平面（x’，y‘，z’），我们会发现两个相似三角形，近平面上的点的z‘=n，根据相似三角形对应边成比例我们可以求出

那么我们将刚刚的变换过程写成齐次坐标的形式：

  此处我们根据齐次坐标的性质，将中间的式子同乘一个z，即得到最右边的式子，这就是原来的点通过变换后得到的新的点的坐标。此时z’我们依然不知道。

我们希望算出来到底是什么样的一个变换矩阵使得这个点的坐标变换成最右边的样子，也就是我们要求出矩阵M_persp->ortho^（4×4）

4*4矩阵除了Z，其它的都是已知的，我们将其写出：

  下面我们来取两个特殊的点。刚刚在一开始已经提到，近平面在挤压之后，任何一个点都不会变，远平面在挤压过程中，Z值不会变，也就是说挤压之后远平面的Z值依然是f（z=f）。

首先我们取近平面上任意一点，由于近平面在挤压之后，任何一个点都不会变，所以此时z就可以用n来替代，得到以下式子：

  所以这个矩阵与近平面上的任意一点相乘的结果第三行是n²，而第一、二行经过齐次坐标的变换后，能将x变为nx，y变为ny，与一开始的通用写法相同，此时第三行的n²显然跟前两行的数x、y没关系，所以这个矩阵可以写成：

  我们再选取远平面的中心点，由于远平面的中心点在挤压之后也不会发生变化，x、y依然是0，z=f，所以同理可以写出矩阵：

联立刚刚的两个式子：

  至此，我们把整个变换的矩阵全部填完了。

参考信息

1、Lecture 04 Transformation Cont._哔哩哔哩_bilibili

2、GAMES101: 现代计算机图形学入门 (ucsb.edu)

3、GAMES101现代计算机图形学入门-闫令琪-随堂笔记-Lecture 04 3DTransformation_闫令琪 transformation-优快云博客

4、GAMES101_Lecture_04 (ucsb.edu)