树的源代码实现（添加、删除、据（前、中）或（中、后）序序列, 给树生成一个根节点并生成树、查找、获得前，中，后序遍历、bfs搜索遍历））

0.二叉搜索树举例

11个整数：100、10、200、0、50、150、300、25、75、30、60

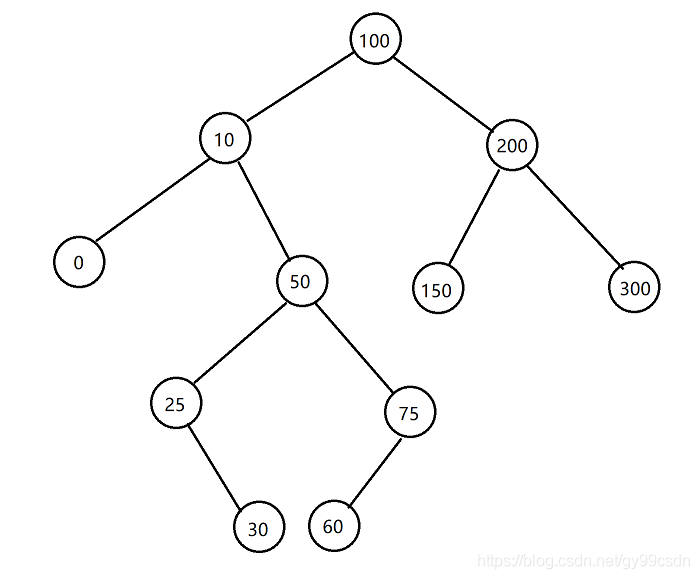
先序：100 、10、0、50、25、30、75、60、200、150、300
中序：0、10、25、30、50、60、75、100、150、200、300
后序：0、30、25、60、75、50、10、150、300、200、100

1.二叉搜索树的成员变量等

/**

• 创建一个二叉搜索树: 链表实现
• <E extends Comparable>: 在二叉搜索树种添加的元素, 应该是可以比较大小的
  */

public class MyBSTree<E extends Comparable<E>> {

    Node root; // 整个二叉搜索树的根节点
    int size;// 整个二叉搜索树的大小
    
     class Node {
        E value;// 值域
        Node left;// 左子树结点
        Node right;// 右子树结点

        public Node(Node left,  E value, Node right) {
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
}

二叉搜索树实现添加功能

 /**
     * 给二叉搜索树实现添加功能
     * @param e
     * @return
     */
    public boolean add(E e){
        // 二叉搜索树中不能是null
        if (e == null) throw new IllegalArgumentException("parame is null");
        // 树是否是空树
        if (size == 0){// 如果是空树, 那么把这个新添加的元素, 作为根节点
            root = new Node(null, e, null);
            size++;
            return true;
        }

        // 必定非空树:
        Node mid = root;
        Node midF = null;
        int com = 0;

        while (mid != null){
            // 把当前遍历结点 和 要存储的值作比较
            com = e.compareTo(mid.value);
            // midF 保存 最终遍历到的存储的位置的父节点
            midF = mid;
            if (com  > 0){
                // e的值 比当前结点大, 向right子树走, 最终存储到right子树上
                mid = mid.right;
            } else if (com < 0){
                // e的值 比当前结点小, 向left子树走, 最终存储到left子树上
                mid = mid.left;
            } else {
                // e的值 和当前结点 相等
                // 理论:
                //    计数法
                //    拉链法
                //    修正的BSTree

                // 不允许存储重复元素: compareTo 结果 = 0
                return  false;
            }
        }

        //把最终元素, 添加到具体位置
       if (com > 0){
           midF.right = new Node(null, e, null);
       }else {
           midF.left = new Node(null, e, null);
       }
       size++;
        return true;
    }

结果输出：

测试输出函数：

        MyBSTree01<Integer> tree = new MyBSTree01<>();
        tree.add(100);
        tree.add(10);
        tree.add(200);
        tree.add(0);
        tree.add(50);
        tree.add(150);
        tree.add(300);
        tree.add(25);
        tree.add(75);
        tree.add(30);
        tree.add(60);
        System.out.println(tree);

输出：

MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=25, left=null, right=Node{value=30, left=null, right=null}}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}, size=11}
添加99后的树:MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=25, left=null, right=Node{value=30, left=null, right=null}}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=Node{value=99, left=null, right=null}}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}, size=1

3.二叉搜索树上删除一个结点

/**
     * 在二叉搜索树上删除一个节点
     *
     * @param e 要删除的节点
     * @return 删除是否成功
     */
    public boolean remove(E e) {
        //参数校验
        if (e == null) throw new IllegalArgumentException("parame is null");
        if (size == 0) throw new RuntimeException("tree is null");
        //找到要删除的节点 和 他的节点
        Node mid = root;//将节点变量指向根节点root
        Node midF = null;//父节点midF置为null
        int com = 0;

        while (mid != null) {
            //把当前遍历节点 和 要删除的值做比较
            com = e.compareTo(mid.value);
            if (com > 0) {
                //midF保存当前遍历到的节点数据，作为下一要删除的节点的父节点
                midF = mid;
                mid = mid.right;//指明下一步的方向
            } else if (com < 0) {
                //midF保存当前遍历到的节点数据，作为下一要删除的节点的父节点
                midF = mid;
                mid = mid.left;
            } else {
                //找到了
                break;//退出循环，执行下一步
            }
        }
        //唯有两种情况走到这一步
        //第一种：没找到mid==null
        if (mid == null) {
            //没找到要删除的节点
            return false;
        }


        //第二种:找到了：mid删除的值，midt要删除值的父节点
        if (mid.left != null && mid.right != null) {//要删除的节点有双子节点
            //找到right子树的最小值
            Node min = mid.right;//将节点变量min指向当前遍历到的节点mid的下一右节点
            Node minF = mid;//将midF指向当前遍历到的节点mid，作为父节点

            //一直在right子树的left方向上一直移动，直到找到一个最小值
            while (min.left != null) {
                minF = min;
                min = min.left;
            }

            //min为最小值，替换
            mid.value = min.value;

            //转成删除min
            mid = min;
            midF = minF;
        }
        //mid要删除的元素
        // Node ch = mid.left != null ? mid.left : mid.right;
        Node ch = mid.right != null ? mid.right : mid.left;//将节点变量ch指向当前遍历要删除节点mid的左或者右方向（）
        if (midF == null) {//判断当前遍历节点mid的父节点是否为空
            //要删除的是一个根节点，并且这个节点 还是单分支
            root = ch;
            size--;
            return true;

        }

        //删除最终的单分支或者叶子结点：删除方式-->上移
        if (midF.left == mid) {//
            midF.left = ch;
        } else {
            midF.right = ch;
        }
        size--;
        return true;
    }

结果输出：

测试输出函数：

System.out.println(tree.remove(25));
        System.out.println("删除值为25后的树:"+tree);
        System.out.println(tree.remove(99));
        System.out.println("删除值为99后的树:"+tree);
        System.out.println(tree.remove(300));
        System.out.println("删除值为300后的树:"+tree);

结果：

true
删除值为25后的树:MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=30, left=null, right=null}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=Node{value=99, left=null, right=null}}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}, size=11}
true
删除值为99后的树:MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=30, left=null, right=null}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}, size=10}
true
删除值为300后的树:MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=30, left=null, right=null}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=null}}, size=9}

4.据前、中序序列, 生成树并确认根节点

/**
     * 根据提供中序和前序序列, 给这个树生成一个根节点
     *
     * @param inOrder
     * @param preOrder
     */
    public void createRoot(ArrayList<E> preOrder, ArrayList<E> inOrder) {
//参数检验
        int count = 1;
        Node rootByPreAndIn = createRootByPreAndIn(preOrder, inOrder, count);

        root = rootByPreAndIn;
        size = inOrder.size();
        System.out.println(rootByPreAndIn);
    }

    //递归构建一个树的方法
    private Node createRootByPreAndIn(List<E> preOrder, List<E> inOrder, int count) {
        //出口
        if (inOrder.size() == 0) {//判断中序数组长度是否为0，及树是否为空
            return null;
        }

        if (inOrder.size() == 1) {
            return new Node(null, inOrder.get(0), null);
        }

        //获得这个递归树的根节点
        E e = preOrder.get(0);

        //获得根节点，在前序序列的位置
        int index = inOrder.indexOf(e);

        List<E> leftInOrder = inOrder.subList(0, index);
        List<E> rightInOrder = inOrder.subList(index + 1, inOrder.size());
        System.out.println("InOrder第" + count + "次递归找到的根节点为" + e);
        System.out.println("leftInOrder第" + count + "次递归" + leftInOrder);
        System.out.println("rightInOrder第" + count + "次递归" + rightInOrder);
        List<E> leftPreOrder = preOrder.subList(1, index + 1);
        List<E> rightPreOrder = preOrder.subList(index + 1, inOrder.size());
        System.out.println("PreOrder第" + count + "次递归找到的根节点为" + e);
        System.out.println("leftPreOrder第" + count + "次递归" + leftPreOrder);
        System.out.println("rightPreOrder第" + count + "次递归" + rightPreOrder);
        Node left = createRootByPreAndIn(leftPreOrder, leftInOrder, ++count);
        Node right = createRootByPreAndIn(rightPreOrder, rightInOrder, ++count);

        Node root = new Node(left, e, right);
        return root;
    }

结果输出：

测试输出函数：

/**
 *
 * 通过前序和中序确定根节点，并创建一个树
 */
        ArrayList<Integer> pre = new ArrayList<>();
        pre.add(100);
        pre.add(10);
        pre.add(0);
        pre.add(50);
        pre.add(25);
        pre.add(30);
        pre.add(75);
        pre.add(60);
        pre.add(200);
        pre.add(150);
        pre.add(300);

        ArrayList<Integer> in = new ArrayList<>();
        in.add(0);
        in.add(10);
        in.add(25);
        in.add(30);
        in.add(50);
        in.add(60);
        in.add(75);
        in.add(100);
        in.add(150);
        in.add(200);
        in.add(300);
         tree.createRoot(pre,in);
        System.out.println("通过前序和中序确定根节点，并创建一个树:"+tree);

输出：

InOrder第1次递归找到的根节点为100
leftInOrder第1次递归[0, 10, 25, 30, 50, 60, 75]
rightInOrder第1次递归[150, 200, 300]
PreOrder第1次递归找到的根节点为100
leftPreOrder第1次递归[10, 0, 50, 25, 30, 75, 60]
rightPreOrder第1次递归[200, 150, 300]
InOrder第2次递归找到的根节点为10
leftInOrder第2次递归[0]
rightInOrder第2次递归[25, 30, 50, 60, 75]
PreOrder第2次递归找到的根节点为10
leftPreOrder第2次递归[0]
rightPreOrder第2次递归[50, 25, 30, 75, 60]
InOrder第4次递归找到的根节点为50
leftInOrder第4次递归[25, 30]
rightInOrder第4次递归[60, 75]
PreOrder第4次递归找到的根节点为50
leftPreOrder第4次递归[25, 30]
rightPreOrder第4次递归[75, 60]
InOrder第5次递归找到的根节点为25
leftInOrder第5次递归[]
rightInOrder第5次递归[30]
PreOrder第5次递归找到的根节点为25
leftPreOrder第5次递归[]
rightPreOrder第5次递归[30]
InOrder第6次递归找到的根节点为75
leftInOrder第6次递归[60]
rightInOrder第6次递归[]
PreOrder第6次递归找到的根节点为75
leftPreOrder第6次递归[60]
rightPreOrder第6次递归[]
InOrder第3次递归找到的根节点为200
leftInOrder第3次递归[150]
rightInOrder第3次递归[300]
PreOrder第3次递归找到的根节点为200
leftPreOrder第3次递归[150]
rightPreOrder第3次递归[300]
Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=25, left=null, right=Node{value=30, left=null, right=null}}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}

5.据中、后序序列, 生成树并确认根节点

/**
     * 根据提供中序和后序序列, 给这个树生成一个根节点
     *
     * @param inOrder
     * @param postOrder
     */
    public void createRoot2(ArrayList<E> inOrder, ArrayList<E> postOrder) {
        // 参数检验
        int count = 1;
        Node rootByInAndPost = createRootByInAndPost(inOrder, postOrder, count);
        root = rootByInAndPost;
        size = inOrder.size();
        System.out.println(rootByInAndPost);

    }

    // 递归构建一个树的方法
    private Node createRootByInAndPost(List<E> inOrder, List<E> postOrder, int count) {
        // TODO: 出口

        if (inOrder.size() == 0) {//若中序数组长度为0
            return null;
        }
        if (inOrder.size() == 1) {//若中序数组长度为1，返回第一个节点
            return new Node(null, inOrder.get(0), null);
        }


        // 获得这个递归树的根节点（每次递归都有一个）
        E e = postOrder.get(inOrder.size() - 1);
        // 获得根结点, 在中序序列的位置
        int index = inOrder.indexOf(e);

        // 中序:
        //      0 ~ index-1 : left中序
        //      index + 1 ~ size-1 : right中序

        // 后序:
        //       0 ~ index -1: left后序
        //      index ~ size-2:  right 后序

        List<E> leftInOrder = inOrder.subList(0, index);//根结点在中序序列的位置左边(0, index)的序列
        List<E> rightInOrder = inOrder.subList(index + 1, inOrder.size());//根结点在中序序列的位置右边(index + 1, inOrder.size())的序列
        System.out.println("InOrder第" + count + "次递归找到的根节点为" + e);
        System.out.println("leftInOrder第" + count + "次递归" + leftInOrder);
        System.out.println("rightInOrder第" + count + "次递归" + rightInOrder);
        List<E> leftPostOrder = postOrder.subList(0, index);//
        List<E> rightPostOrder = postOrder.subList(index, inOrder.size() - 1);
        System.out.println("PostOrder第" + count + "次递归找到的根节点为" + e);
        System.out.println("leftPostOrder第" + count + "次递归" + leftPostOrder);
        System.out.println("rightPostOrder第" + count + "次递归" + rightPostOrder);
        Node left = createRootByInAndPost(leftInOrder, leftPostOrder, ++count);

        Node right = createRootByInAndPost(rightInOrder, rightPostOrder, ++count);

        Node root = new Node(left, e, right);

        return root;
    }

结果输出：

/**
 *
 * 通过中序和后序确定根节点，并创建一个树
 */

 ArrayList<Integer> in = new ArrayList<>();
        in.add(0);
        in.add(10);
        in.add(25);
        in.add(30);
        in.add(50);
        in.add(60);
        in.add(75);
        in.add(100);
        in.add(150);
        in.add(200);
        in.add(300);

        ArrayList<Integer> post = new ArrayList<>();
        post.add(0);
        post.add(30);
        post.add(25);
        post.add(60);
        post.add(75);
        post.add(50);
        post.add(10);
        post.add(150);
        post.add(300);
        post.add(200);
        post.add(100);
        tree.createRoot2(in,post);
        System.out.println("通过中序和后序确定根节点，并创建一个树:"+tree);

输出;

InOrder第1次递归找到的根节点为100
leftInOrder第1次递归[0, 10, 25, 30, 50, 60, 75]
rightInOrder第1次递归[150, 200, 300]
PostOrder第1次递归找到的根节点为100
leftPostOrder第1次递归[0, 30, 25, 60, 75, 50, 10]
rightPostOrder第1次递归[150, 300, 200]
InOrder第2次递归找到的根节点为10
leftInOrder第2次递归[0]
rightInOrder第2次递归[25, 30, 50, 60, 75]
PostOrder第2次递归找到的根节点为10
leftPostOrder第2次递归[0]
rightPostOrder第2次递归[30, 25, 60, 75, 50]
InOrder第4次递归找到的根节点为50
leftInOrder第4次递归[25, 30]
rightInOrder第4次递归[60, 75]
PostOrder第4次递归找到的根节点为50
leftPostOrder第4次递归[30, 25]
rightPostOrder第4次递归[60, 75]
InOrder第5次递归找到的根节点为25
leftInOrder第5次递归[]
rightInOrder第5次递归[30]
PostOrder第5次递归找到的根节点为25
leftPostOrder第5次递归[]
rightPostOrder第5次递归[30]
InOrder第6次递归找到的根节点为75
leftInOrder第6次递归[60]
rightInOrder第6次递归[]
PostOrder第6次递归找到的根节点为75
leftPostOrder第6次递归[60]
rightPostOrder第6次递归[]
InOrder第3次递归找到的根节点为200
leftInOrder第3次递归[150]
rightInOrder第3次递归[300]
PostOrder第3次递归找到的根节点为200
leftPostOrder第3次递归[150]
rightPostOrder第3次递归[300]
Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=25, left=null, right=Node{value=30, left=null, right=null}}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}
通过中序和后序确定根节点，并创建一个树:MyBSTree01{root=Node{value=100, left=Node{value=10, left=Node{value=0, left=null, right=null}, right=Node{value=50, left=Node{value=25, left=null, right=Node{value=30, left=null, right=null}}, right=Node{value=75, left=Node{value=60, left=null, right=null}, right=null}}}, right=Node{value=200, left=Node{value=150, left=null, right=null}, right=Node{value=300, left=null, right=null}}}, size=11}

6.查找指定值的节点并返回

/**
     * 查找指定值的节点，并返回该节点
     */
    public Node findNode(E e) {
        if (e == null) throw new IllegalArgumentException("e is null");
        if (root == null) throw new EmptyStackException();
        Node mid = root;
        //遍历找到待查找元素的节点
        while (mid != null) {
            int com = e.compareTo(mid.value);
            if (com > 0) {
                mid = mid.right;
            } else if (com < 0) {
                mid = mid.left;
            } else
                break;
        }
        //没找到
        if (mid == null)
            return null;
        else
            return mid;
    }

结果输出：

 System.out.println("查找节点:"+tree.findNode(75));

查找节点:Node{value=75, left=Node{value=60, left=null, right=null}, right=null}

7.前序遍历

（1）栈实现

/**
     * 获得该BSTree 前序遍历结果,栈实现
     *
     * @return
     */
    public List<E> preOrder() {
//存储遍历结果（出栈的元素）
        List<E> list = new ArrayList<>();
        //辅助的栈，用来帮助遍历
        LinkedList<Node> stack = new LinkedList<>();

        //根节点入栈
        stack.push(root);
        //遍历栈中元素
        while (!stack.isEmpty()) {
            Node pop = stack.pop();
            list.add(pop.value);
            if (pop.right != null) {
                stack.push(pop.right);
            }
            if (pop.left != null) {
                stack.push(pop.left);
            }
        }
        return list;
    }

结果输出：同下

（2）递归实现

 /**
     * 实现前序遍历: 使用递归
     *
     * @return 遍历结果
     */
    public List<E> preOrder2() {
        List<E> list = new ArrayList<>();
        preOrder2(list, root);
        return list;
    }

    public void preOrder2(List<E> list, Node root) {
        if (root == null) {//递归出口
            return;
        }
        list.add(root.value);//先遍历根节点
        preOrder2(list, root.left);//遍历left子树
        preOrder2(list, root.right);//遍历right子树
    }

结果输出：

//获得该BSTree 使用栈来辅助调用，List存储实现前序遍历结果,preOrder()来测试

        System.out.println("栈来辅助调用，List存储实现前序遍历结果:"+tree.preOrder());
        //递归获得该BSTree 前序遍历结果,preOrder2()来测试
        System.out.println("递归实现前序遍历结果:"+tree.preOrder2());

栈来辅助调用，List存储实现前序遍历结果:[100, 10, 0, 50, 25, 30, 75, 60, 200, 150, 300]
递归实现前序遍历结果:[100, 10, 0, 50, 25, 30, 75, 60, 200, 150, 300]

8.中序遍历

（1）栈实现

 /**
     * 中序遍历:  利用栈来实现
     *
     * @return 遍历的序列
     */
    public List<E> inOrder() {
        //创建存储遍历结果的list
        ArrayList<E> list = new ArrayList<>();
        //创建一个栈用来遍历
        LinkedList<Node> stack = new LinkedList<>();

//标记节点
        Node flagNode = root;

        //循环条件：栈不为空，或者标记节点不为null
        while (!stack.isEmpty() || flagNode != null) {

            while (flagNode != null) {//直到flagNode节点为null出循环
                stack.push(flagNode);//flagNode节点入栈
                flagNode = flagNode.left;//flagNode节点的下一左节点
            }
            //出栈一个元素，遍历
            Node pop = stack.pop();
            list.add(pop.value);


            //让标记节点，指向出栈节点的right节点
            flagNode = pop.right;
        }

        return list;
    }

结果输出：同下

（2）递归实现

 /**
     * 中序遍历:  利用递归来实现
     *
     * @return 遍历的序列
     */
    public List<E> inOrder2() {
        ArrayList<E> list = new ArrayList<>();
        inOrder2(list, root);
        return list;

    }

    public void inOrder2(ArrayList<E> list, Node root) {
        if (root == null) {
            return;
        }

        inOrder2(list, root.left);
        list.add(root.value);
        inOrder2(list, root.right);
    }

结果输出：

//中序遍历:  利用栈来实现,inOrder()
        System.out.println("栈来实现中序遍历:"+tree.inOrder());

        //中序遍历:  利用递归来实现
        System.out.println("递归来实现中序遍历:"+tree.inOrder2());

输出;

栈来实现中序遍历:[0, 10, 25, 30, 50, 60, 75, 100, 150, 200, 300]
递归来实现中序遍历:[0, 10, 25, 30, 50, 60, 75, 100, 150, 200, 300]

9.后序遍历

（1）栈实现

 /**
     * BSTree 的 后序遍历--- 栈
     *
     * @return 遍历结果
     */
    public List<E> postOrder() {
        // 存储遍历结果
        ArrayList<E> list = new ArrayList<>();
        // 临时用来遍历的栈
        LinkedList<Node> stack = new LinkedList<>();
        // 根节点入栈
        stack.push(root);
// 循环遍历
        while (!stack.isEmpty()) {
            Node pop = stack.pop();
            // 遍历(头插法)
            list.add(0, pop.value);
            // 让遍历元素的左右子元素入栈
            if (pop.left != null) {
                stack.push(pop.left);
            }
            if (pop.right != null) {
                stack.push(pop.right );
            }
        }
        return list;

    }

结果输出：同下

（2）递归实现

/**
     * BSTree的后序遍历 --- 递归实现
     *
     * @return: 遍历结果
     */
    public List<E> postOrder2(){
        ArrayList<E> list=new ArrayList<>();
        postOrder2(list,root);
        return list;
    }
    public void postOrder2(ArrayList<E> list,Node root){
        if (root==null){
            return;
        }
        //遍历left子树
        postOrder2(list,root.left);
        //遍历right子树
        postOrder2(list,root.right);
        //遍历根节点
        list.add(root.value);

    }

结果输出：

//后序遍历--- 栈实现postOrder
        System.out.println("栈来实现后序遍历:"+tree.postOrder());

        //后序遍历--- 递归实现postOrder
        System.out.println("递归来实现后序遍历:"+tree.postOrder2());

输出：

栈来实现后序遍历:[0, 30, 25, 60, 75, 50, 10, 150, 300, 200, 100]
递归来实现后序遍历:[0, 30, 25, 60, 75, 50, 10, 150, 300, 200, 100]

10.广度（层级）优先搜索bfs

 /**
     * 层级遍历, 广度遍历, 广度优先搜索
     */
    public List<E> bfsOrder(){
        // 创建一个存储遍历结果集合
        ArrayList<E> list=new ArrayList<>();
        // 创建队列
        LinkedList<Node> queue=new LinkedList<>();
// 根节点入队列
        queue.offer(root);
// 循环遍历
        while (!queue.isEmpty()){
            // 出队列一个元素, 遍历
            Node poll=queue.poll();
            list.add(poll.value);
            // 左右子结点入队列
            if (poll.left!=null) queue.offer(poll.left);
            if (poll.right!=null) queue.offer(poll.right);

        }
        return list;
    }

结果输出：

//层级遍历, 广度遍历, 广度优先搜索bfsOrder()
        System.out.println("广度优先搜索遍历:"+tree.bfsOrder());

输出;

广度优先搜索遍历:[100, 10, 200, 0, 50, 150, 300, 25, 75, 30, 60]