SVM解释：一、SVM的整体框架

支持向量机（Support Vector Machine）是一种非常重要的分类方法，大的范畴上讲，属于监督学习。它最早由Vapnik等人在1992年提出，已经发展了近30年。尽管它的训练速度偏慢，但是由于其对复杂非线性数据的强大的建模能力，依然在很多领域，包括手写数字识别，对象识别，基准时间序列预测检验等有着非常广泛的应用。可以说，任何一种二分类的问题都在理论上都可以用SVM解决。

当然，SVM如此强大的原因也要归功于它背后巧妙而又复杂的数学原理，如果没有相关的基础，学习SVM是一件费时费力的事情。和机器学习中那些相对简单的分类算法不同，学习SVM的过程是非常浩繁的。这一点从我写的这个SVM的学习笔记就能看出来：我前后一共用了5篇博文。因此也实在难免出错，如果有心的读者发现了我的错误，或者觉得内容有需要改进的地方，还望不吝赐教。

本文类似于一篇引言，我将简单介绍一下什么是SVM，它用来做什么，大致的框架是什么样的，以及我这5篇博文都大概说了些什么。以求在最大程度上给大家，也给未来健忘的我自己一个清晰的概念。

1. SVM是什么

支持向量机（简称SVM）是一种分类算法。它主要应用于二分类问题，通过定位两类数据在几何空间中的边缘，来确定分类器。一个简单的例子如Fig.1所示，黑点和白点分别代表两类数据，SVM的目的就是要找到一个超平面，比如Fig.1中的红色虚线（后面我们会知道，对于线性不可分数据来说，实际要找的是一个曲面），恰好能“最好地”将两类数据分开，这样的超平面（或曲面）就是SVM分类器，找到分类器后，我们自然可以依据测试数据与分类器的位置关系，预测它的分类。比如Fig.1中，如果测试数据在虚线以上，就属于黑点这个类；若在虚线以下，就属于白点这个类。

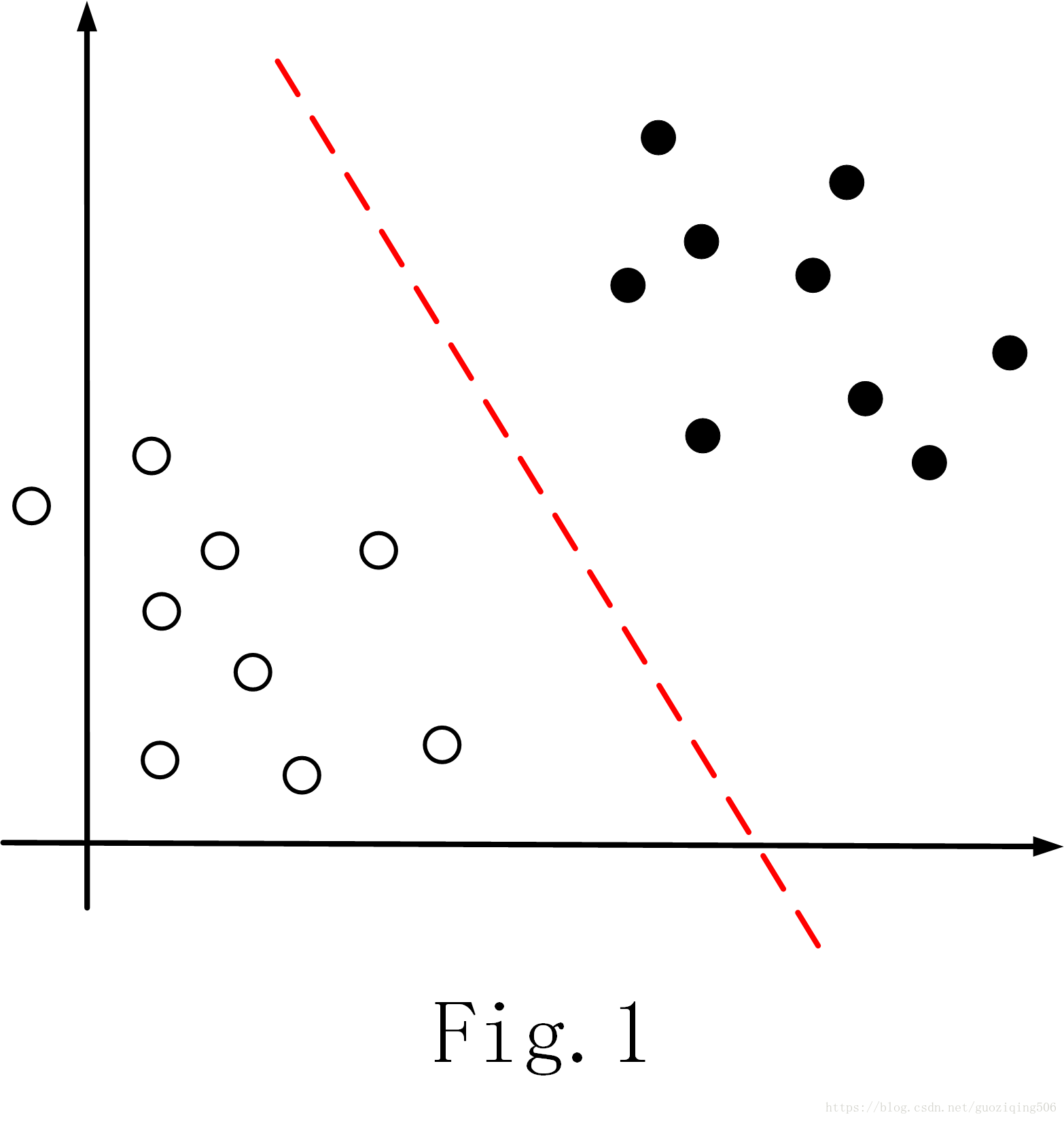
所以，核心的问题是，什么样的超平面（或曲面）是“最好的”呢？直观感受告诉我们，这样的超平面在两类数据之间，同时应该具备如下两个条件：

• 最近距离最远：两类数据中，每类数据都有一个点距离该超平面的距离是最近的，而“最好的”超平面要这个两个最近距离的和尽可能的远；
• 等距：超平面距离两类数据最近的点的距离是相等的；

上面这两个条件也是SVM最基本的原理，就是找到所谓的“最大间隔”。

你看，分类问题现在转换成了一个求“最大”的问题，这显然是一个优化问题，而怎么解这个优化问题（即怎么找到这样“最好的”平面或者曲面）就是SVM的全部内容了。

2. 二分类转多分类的策略

在介绍SVM的整体框架之前，我先在这里插一点别的东西，那就是二分类问题到多分类问题的转换策略。前面说SVM是典型的解决二分类问题的算法，那你肯定会产生疑问，能不能把它拓展到多分类问题呢？其实不仅是SVM，大多二分类问题都可以通过“一对一”和“一对多”两种策略转换到多分类问题中。

2.1 一对一

现有训练集$X$，其中的数据元组共属于$n$个类。所谓“一对一”策略就是将类别两两组合，构成$\frac{n(n - 1)}{2}$种组合。举个例子，现在数据元组共属于4个类$A, B, C, D$，那就有6种组合： AB,AC,AD,BC