声明:
本文是我在学习 NumPy 科学计算库相关知识过程中,结合个人实践与理解整理的学习笔记,参考了NumPy 快速入门 — NumPy v2.4 手册 - NumPy 科学计算库。本文仅用于个人学习交流使用,不涉及任何商业用途。
一、堆叠数组
(1)np.vstack():
对于二维数组,垂直堆叠(沿axis=0,行方向)(沿行方向操作,行数变化)(上下拼),堆叠的两个数组列数一致,否则上下拼不到一起。
(2)np.hstack():
对于二维数组,水平堆叠(沿axis=1,列方向 )(沿列方向操作,列数变化)(左右拼 ),堆叠的两个数组行数一致,否则左右拼不到一起。
(3)np.dstack():
对于二维数组,后面堆叠(沿axis=2,深度方向,增加深度维度),多个数组在 “垂直于行列的方向” 拼接(可以理解为 “在现有数组的‘后面’叠层”)。 待堆叠的数组,前面的维度(行、列)必须完全一致,堆叠后会新增 / 扩展 “第三个维度(深度)” 。
- 若堆叠一维数组:先将每个一维数组转为
(长度, 1)的二维数组,再沿axis=2堆叠 → 结果是(长度, 1, 堆叠数); - 若堆叠二维数组:直接沿
axis=2堆叠 → 结果是(行数, 列数, 堆叠数)
dstack 是沿 “深度” 拼接数组,适合合并 “同尺寸的二维数据(如图像通道、特征矩阵)”,最终得到包含 “层 / 通道” 信息的三维数组。
import numpy as np
# 两个一维数组(长度都是3)
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# dstack堆叠
res = np.dstack((a, b))
print("a的形状:", a.shape) # (3,)
print("b的形状:", b.shape) # (3,)
print("堆叠后形状:", res.shape) # (3, 1, 2) → 长度3,列1,深度2
print("堆叠结果:")
print(res)
# 输出:
# [[[1 4]]
# [[2 5]]
# [[3 6]]]
# 两个2行3列的二维数组(模拟灰度图)
img1 = np.array([[10, 20, 30], [40, 50, 60]]) # 灰度图1
img2 = np.array([[11, 21, 31], [41, 51, 61]]) # 灰度图2
# dstack堆叠(沿深度维度合并通道)
color_img = np.dstack((img1, img2))
print("img1形状:", img1.shape) # (2, 3)
print("img2形状:", img2.shape) # (2, 3)
print("堆叠后形状:", color_img.shape) # (2, 3, 2) → 2行3列2通道
print("堆叠结果:")
print(color_img)
# 输出:
# [[[10 11]
# [20 21]
# [30 31]]
#
# [[40 41]
# [50 51]
# [60 61]]](4)np.column_stack():
对于二维数组,等价于np.hstack(),沿列方向拼接(列数变化)。同时它也可以将1维数组作为列堆叠到2维数组上。 1D数组的元素个数=2D数组的行数 。同时也可以将1D与1D按列堆叠。
import numpy as np
np.random.seed(42)
a=np.random.randint(0,10,size=(2,3))
print(a) #[[6 3 7]
# [4 6 9]]
b=np.random.randint(0,10,size=(3,3))
print(b) #[[2 6 7]
# [4 3 7]
# [7 2 5]]
c=np.vstack((a,b))
print(c) #[[6 3 7]
# [4 6 9]
# [2 6 7]
# [4 3 7]
# [7 2 5]]
d=np.random.randint(0,10,size=(2,2))
print(d) #[[4 1]
# [7 5]]
print(np.hstack((a,d))) #[[6 3 7 4 1]
# [4 6 9 7 5]]
print(np.column_stack((a,d))) #[[6 3 7 4 1]
# [4 6 9 7 5]]a=np.random.randint(0,10,size=(2,))
b=np.random.randint(0,10,size=(2,3))
print(a) #[6 3]
print(b) #[[7 4 6]
# [9 2 6]]
print("1D堆叠到2D",np.column_stack((a,b))) #1D堆叠到2D [[6 7 4 6]
# [3 9 2 6]]
c=np.random.randint(0,10,size=(2,))
print(c) #[7 4]
print("1D堆叠到1D",np.column_stack((a,c))) #1D堆叠到1D [[6 7]
# [3 4]](5)np.concatenate:
可以指定轴来拼接函数,支持任意维度数组。
对于二维数组:np.concatenate((a,b),axis=0),即沿行拼接,等价于vstack
np.concatenate((a,b),axis=1),即沿列拼接,等价于hstack
3D数组的维度通常记为 (块数, 行数, 列数),对应的 axis 索引是:
axis=0:沿 块 维度 拼接(块数增加);(把b的2个块“追加”到a的2个块后面)axis=1:沿 行 维度 拼接(行数增加);(把b的3行“追加”到a的3行后面(每个块内的行数变多))axis=2:沿 列 维度 拼接(列数增加)。(把b的4列“追加”到a的4列后面(每个块的每行列数变多))- 拼接三维数组时,必须保证:除了
axis指定的维度外,其他两个维度的长度完全一致。# 构造两个三维数组:shape=(2, 3, 4) → 2个块、3行、4列 a = np.fromfunction(lambda k, i, j: 100*k + 10*i + j, (2, 3, 4), dtype=int) b = np.fromfunction(lambda k, i, j: 100*k + 10*i + (j+4), (2, 3, 4), dtype=int) print("原数组a的shape:", a.shape) # 输出 (2, 3, 4) print("原数组b的shape:", b.shape) # 输出 (2, 3, 4) print("原数组a:", a)# 原数组a [[[ 0 1 2 3] # [ 10 11 12 13] # [ 20 21 22 23]] # [[100 101 102 103] # [110 111 112 113] # [120 121 122 123]]] print("原数组b:", b) # 原数组b: [[[ 4 5 6 7] # [ 14 15 16 17] # [ 24 25 26 27]] # [[104 105 106 107] # [114 115 116 117] # [124 125 126 127]]] res_axis0 = np.concatenate((a, b), axis=0) print("\naxis=0拼接后的shape:", res_axis0.shape) # 输出 (4, 3, 4) # 效果:把b的2个块“追加”到a的2个块后面 print("\naxis=0拼接后:", res_axis0)# axis=0拼接后: # [[[ 0 1 2 3] # [ 10 11 12 13] # [ 20 21 22 23]] # [[100 101 102 103] # [110 111 112 113] # [120 121 122 123]] # [[ 4 5 6 7] # [ 14 15 16 17] # [ 24 25 26 27]] # [[104 105 106 107] # [114 115 116 117] # [124 125 126 127]]] res_axis1 = np.concatenate((a, b), axis=1) print("axis=1拼接后的shape:", res_axis1.shape) # 输出 (2, 6, 4) # 效果:把b的3行“追加”到a的3行后面(每个块内的行数变多) print("axis=1拼接后:", res_axis1)# axis=1拼接后: # [[[ 0 1 2 3] # [ 10 11 12 13] # [ 20 21 22 23] # [ 4 5 6 7] # [ 14 15 16 17] # [ 24 25 26 27]] # [[100 101 102 103] # [110 111 112 113] # [120 121 122 123] # [104 105 106 107] # [114 115 116 117] # [124 125 126 127]]] res_axis2 = np.concatenate((a, b), axis=2) # 效果:把b的4列“追加”到a的4列后面(每个块的每行列数变多) print("axis=2拼接后的shape:", res_axis2.shape) # 输出 (2, 3, 8) print("axis=2拼接后:", res_axis2)# axis=2拼接后: # [[[ 0 1 2 3 4 5 6 7] # [ 10 11 12 13 14 15 16 17] # [ 20 21 22 23 24 25 26 27]] # [[100 101 102 103 104 105 106 107] # [110 111 112 113 114 115 116 117] # [120 121 122 123 124 125 126 127]]]
二、切割数组
1. np.vsplit():
垂直切割(axis=0,沿行方向,行数变化,二维数组专用),把数组按 “行” 分成多个子数组。
- 要求:数组的行数能被 “拆分份数” 整除(否则会报错)。
2. np.hsplit():
水平切割(axis=1,沿列方向,列数变化,二维数组专用),把数组按 “列” 分成多个子数组。
- 要求:数组的列数能被 “拆分份数” 整除(否则会报错)。
可以用np.hsplit(a,(3,4))来从d的第三列第四列之后分割数组。
x=np.arange(1,25).reshape((2,12))
b=np.hsplit(x,3) #[array([[ 1, 2, 3, 4],
# [13, 14, 15, 16]]),
# array([[ 5, 6, 7, 8],
# [17, 18, 19, 20]]),
# array([[ 9, 10, 11, 12],
# [21, 22, 23, 24]])]
print(b)
c=np.hsplit(x,(3,4))
print(c) #[array([[ 1, 2, 3],
# [13, 14, 15]]),
# array([[ 4], [16]]),
# array([[ 5, 6, 7, 8, 9, 10, 11, 12],
# [17, 18, 19, 20, 21, 22, 23, 24]])]3. np.array_split():
通用切割(支持任意维度 + 不均等拆分)
- 任意维度的数组(二维、三维等);、
- 允许指定哪个轴进行分割;
- 不均等拆分(数组长度不能被份数整除时,自动调整子数组的长度,不会报错)。
import numpy as np
# 5个学生的成绩表(5行3列)
scores = np.array([
[85,90,88], [78,82,80], [92,88,95],
[80,85,82], [75,79,76]
])
# 沿行方向(axis=0)拆分为2份(前3行、后2行)
class1, class2 = np.vsplit(scores, 2) # 注意:5不能被2整除,这里实际会报错!
# 正确操作:拆分为“能整除的份数”,比如拆分为5份(每个学生单独一行)
students = np.vsplit(scores, 5)
print("拆分后的第一个学生成绩:", students[0]) # 输出 [[85 90 88]]
# 5行3列的成绩表(数学、英语、语文)
scores = np.array([
[85,90,88], [78,82,80], [92,88,95],
[80,85,82], [75,79,76]
])
# 沿列方向(axis=1)拆分为2份(数学列、英语+语文列)
math, others = np.hsplit(scores, [1]) # 用[1]表示“在列索引1的位置切割”
print("数学成绩列:")
print(math) # 输出5行1列的数组(仅数学成绩)
# 5个学生的成绩表(5行3列)
scores = np.array([
[85,90,88], [78,82,80], [92,88,95],
[80,85,82], [75,79,76]
])
# 沿行方向(axis=0)拆分为2份(不均等:前3行、后2行)
class1, class2 = np.array_split(scores, 2, axis=0)
print("class1的行数:", class1.shape[0]) # 输出3
print("class2的行数:", class2.shape[0]) # 输出2(自动调整长度)三、广播
1.自动广播
- 广播的核心:自动扩展形状不匹配但兼容的数组,使其能做算术运算;
- 判断规则:从最后一维开始(从数组形状的 “最右侧维度” 开始,向左依次比对每个维度的长度”),维度长度要么相等、要么一个是 1、要么一个缺失;
判断两个数组能否广播时,需要把两个数组的形状都补到 “维度数相同”(缺维度的在左边补 1),然后从最右侧的维度(最后一维)开始,向左逐个比对每个位置的维度长度。
广播的第一条规则是,如果所有输入数组的维度数不相同,则会在较小数组的形状前面反复添加“1”,直到所有数组都具有相同的维度数。
广播的第二条规则确保沿特定维度的尺寸为 1 的数组的行为,就好像它们在那个维度上具有最大形状的数组的尺寸一样。“广播”数组在该维度上假定其元素值相同。
最常用场景:标量和数组运算、一维数组和二维数组运算(比如给每行 / 每列加固定值)。
a = np.array([[1,2], [3,4], [5,6]]) # 二维数组(3行2列)
b = 2 # 标量(无维度)
# 标量b被广播成(3,2)的数组,每个元素都是2,再和a相乘
result = a * b
print(result)
# 输出:
# [[ 2 4]
# [ 6 8]
# [10 12]]
a = np.array([[1,2], [3,4], [5,6]])# 二维数组(3行2列)
b = np.array([10, 20])# 一维数组(长度2,对应二维数组的“列维度”)
# b被广播成(3,2)的数组:[[10,20], [10,20], [10,20]],再和a相加
result = a + b
print(result)
# 输出:
# [[11 22]
# [13 24]
# [15 26]]
a = np.array([[1], [2], [3]])# 数组1:(3,1)(3行1列)
b = np.array([[10, 20]])# 数组2:(1,2)(1行2列)
# a广播成(3,2):[[1,1], [2,2], [3,3]]
# b广播成(3,2):[[10,20], [10,20], [10,20]]
result = a + b# 相加后得到结果
print(result)
# 输出:
# [[11 21]
# [12 22]
# [13 23]]
a = np.array([[1,2,3], [4,5,6]])# 数组1:(2,3)(2行3列)
b = np.array([[1,2], [3,4], [5,6]])# 数组2:(3,2)(3行2列)
# 对比维度:最后一维3 vs 2(既不相等,也没有1)→ 不兼容
result = a + b # 报错:ValueError: operands could not be broadcast together with shapes (2,3) (3,2)2. np.ix_()
将多个一维数组,转换为 “广播兼容的多维索引数组”,让它们可以直接运算。
结合 数组的 “维度顺序”+ np.ix_()的参数顺序,给每个一维数组 “分配一个专属维度”,只让这个维度用数组本身的长度(>1),其他维度都用 1 填充。
np.ix_()接收的参数顺序是(a, b, c),对应三维数组的 第 1 维度、第 2 维度、第 3 维度。
ax的形状是(4, 1, 1),bx的形状是(1, 3, 1),cx的形状是(1, 1, 5)。
让这三个数组满足广播规则,运算时会自动扩展成相同的形状(4,3,5)
a = np.array([2, 3, 4, 5])
b = np.array([8, 5, 4])
c = np.array([5, 4, 6, 8, 3])
ax, bx, cx = np.ix_(a, b, c)
print(ax) #array([[[2]]
#[[3]]
# [[4]]
# [[5]]])
print(bx) #array([[[8]
#[5]
# [4]]])
print(cx) #array([[[5, 4, 6, 8, 3]]])
ax.shape, bx.shape, cx.shape #((4, 1, 1), (1, 3, 1), (1, 1, 5))
result = ax + bx * cx
result
result[3, 2, 4] #17
a[3] + b[2] * c[4] #17四、视图与拷贝
1.a.view():
创建原数组的视图(view),与原数组共享同一块内存,修改视图会影响原数组。
2.a.copy():
创建原数组的副本(copy),与原数组内存完全独立。
a=np.array([[1,2],[3,4]])
print(a) #[[1 2]
# [3 4]]
a_view=a.view()
a_copy=a.copy()
print(a_view) #[[1 2]
# [3 4]]
a_view[0]=99
print(a) #[[99 99]
# [ 3 4]]
a_copy[0]=90
print(a) #[[99 99]
# [ 3 4]]五、技巧
1.自动重塑
更改数组的维度,可以省略其中一个尺寸(-1),该尺寸将自动推断
a = np.arange(30)
b = a.reshape((2, -1, 3)) # -1 means "whatever is needed"
b.shape #(2, 5, 3)
2.向量堆叠
二维数组直接用np.vstack、np.hstack、np.dstack
x = np.arange(0, 10, 2)
y = np.arange(5)
m = np.vstack([x, y])
m #array([[0 2 4 6 8]
# [0 1 2 3 4]])
xy = np.hstack([x, y])
xy #array([0 2 4 6 8 0 1 2 3 4])
c=np.dstack([x,y])
print(c) #[[[0 0]
# [2 1]
# [4 2]
# [6 3]
# [8 4]]]3.访问文档
help(max):
适用于你创建的函数和其他对象。只需记住在函数中使用字符串字面量(""" """ 或 ''' ''' 括起你的文档)包含文档字符串
六、直方图
用plt.hist(values,bins,density=True)来生成归一化直方图,bins=50:把数据分成50个区间(柱子);density=True:把直方图归一化,(密度,所有柱子面积之和为1)
(n,bins)=np.histogram(v,bins=50,density=True):
np.histogram:计算出每个区间的 “密度值(n)” 和 “区间边界(bins)”
n:长度为 50 的数组,对应 “50 个区间(bin)内数据的归一化密度值”(因为density=True,所有区间的密度面积之和为 1);bins:长度为 51 的数组,对应 “50 个区间的边界值”(比如第 1 个区间是bins[0]~bins[1],第 2 个是bins[1]~bins[2],以此类推)。
plt.plot(0.5 * (bins[1:] + bins[:-1]), n):
这是用 Matplotlib 绘制直方图的轮廓折线,核心是计算每个区间的 “中点” 作为折线的 x 坐标:
bins[1:]:取bins去掉第一个元素(即所有区间的 “右边界”);bins[:-1]:取bins去掉最后一个元素(即所有区间的 “左边界”);0.5 * (bins[1:] + bins[:-1]):计算每个区间的中点(比如区间是[1.0, 2.0],中点就是1.5);plt.plot(...):最终以 “区间中点” 为 x 轴、“区间密度值 n” 为 y 轴,绘制折线,展示数据分布的轮廓。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
mu=2
sigma=0.5
v=np.random.normal(mu,sigma,10000) #生成正态分布数据
plt.hist(v,bins=50,density=True) #绘制归一化直方图
(n,bins)=np.histogram(v,bins=50,density=True) #计算数据直方图统计量
plt.plot(0.5*(bins[1:]+bins[:-1]),n)
plt.show()七、使用数学公式
均方误差公式:
在numpy中是error=(1/n)*np.sum(np.square(predictions-labels)),只需要predictions和labels大小相同。
可视化:


八、保存和加载Numpy对象
将数组保存到磁盘并在不重新运行代码的情况下将其加载回来。
np.save():确保指定要保存的数组和文件名。它保存的后缀是.npy。
np.load():加载.npy文件,需指定文件名
a = np.array([1, 2, 3, 4, 5, 6])
np.save('filename', a)
b = np.load('filename.npy')
print(b) #[1 2 3 4 5 6]np.savetxt():将 NumPy 数组保存为普通文本文件,如 **.csv** 或 **.txt** 文件
np.loadtxt():加载如 **.csv** 或 **.txt** 文件文件,需指定文件名
a=np.array([1,2,3,4])
np.savetxt("test.csv",a)
b=np.loadtxt("test.csv")
print(b) #[1. 2. 3. 4.]np.savez():确保指定要保存的数组和文件名。它保存的后缀是.npz
.npy/.npz(NumPy 专属二进制格式):优势是体积小、读取速度快(适合大规模数据的本地存储)。
示例 1:用 np.savetxt() 保存带头部 / 尾部、指定分隔符的文件
先创建数据,再保存为 CSV 格式(逗号分隔),并添加头部说明、尾部注释:
delimiter:统一保存 / 加载时的数据分隔规则(避免因分隔符不匹配导致加载失败);header/footer:给文本文件添加说明信息(不影响数据本身,以注释形式存在);skiprows(loadtxt参数):加载时跳过注释行 / 无关行,确保只读取数据部分
import numpy as np
# 准备测试数据(2维数组)
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 保存为CSV文件:指定分隔符为逗号,添加头部/尾部
np.savetxt(
'test_data.csv', # 保存的文件名
data, # 要保存的数据
delimiter=',', # 数据分隔符(CSV用逗号)
header='这是测试数据的头部说明(列:a,b,c)', # 头部注释
footer='这是测试数据的尾部注释(共3行数据)' # 尾部注释
)结果如下:
示例 2:用 np.loadtxt() 加载指定分隔符、跳过头部的文件
加载上面保存的 test_data.csv,需指定分隔符,并跳过头部注释行:
# 加载CSV文件:指定分隔符,跳过头部1行注释
loaded_data = np.loadtxt(
'test_data.csv',
delimiter=',', # 与保存时的分隔符一致
skiprows=1 # 跳过头部的1行注释(#开头的行)
)
print(loaded_data)
# 输出:
# [[1. 2. 3.]
# [4. 5. 6.]
# [7. 8. 9.]]np.genfromtxt():相比于np.loadtxt()更灵活,能处理缺失值、不规则分布符号(空格、逗号、制表符混合)、混合数据类型(字符串、整数、浮点数)、能读取列名,返回结构化数组(方便按列名访问数据)等场景,将文本文件解析为Numpy数组(缺失值默认填充为NaN)
import numpy as np
data=np.genfromtxt("test_data.csv",
delimiter=',',
names=True,#自动读取表头第一行作为列名,并跳过表头行
missing_values=[''],# 把“空字符串”识别为缺失值
filling_values=0,# 缺失值填充为0(默认是NaN)
dtype=[('name','U10'),# 指定name列为字符串类型(U10表示最多10个字符的Unicode字符串)
('age',float),# age列为浮点型
('score',float)])# score列为浮点型
print(data) #[('Alice', 20., 85.) ('Bob', 0., 90.) ('Charlie', 22., 0.)]九、导入导出CSV
利用pandas
1.导入CSV
pd.read_csv("test_data.csv", header=0):
读取test_data.csv文件,header=0表示 “文件的第 1 行是表头(列名)”,最终得到一个 Pandas 的 DataFrame(表格型数据结构)。.values:将 DataFrame 转换为NumPy 数组(方便后续用 NumPy 做数值计算)。
import pandas as pd
x=pd.read_csv('test_data.csv',header=0).values#表示 “文件的第 1 行是表头(列名)
print(x)
#[['Alice' 20.0 85.0]
# ['Bob' nan 90.0]
# ['Charlie' 22.0 nan]](1)将全部空值填充为0。
import pandas as pd
df=pd.read_csv('test_data.csv',header=0)#表示 “文件的第 1 行是表头(列名)
df_filled=df.fillna(0) #将空值填为0
print(df_filled)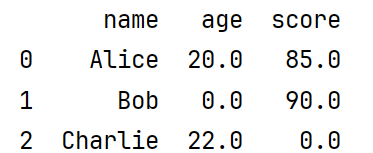
(2)将指定列的空值填充为0。
df['age']=df['age'].fillna(0) #指定列填充为0
print(df)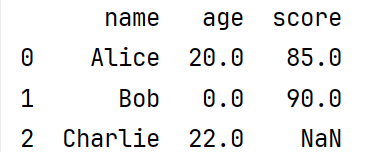

pd.read_csv("test_data.csv", usecols=['name','score']).values:
读取 CSV 的指定列并转为 NumPy 数组。
b=pd.read_csv('test_data.csv',usecols=['name','score']).values
print(b)#[['Alice' 85.0]
#['Bob' 90.0]
# ['Charlie' nan]]2.导出CSV
np.random.seed(42)
a=np.random.random(size=(5,4))
print(a)
#[[0.37454012 0.95071431 0.73199394 0.59865848]
# [0.15601864 0.15599452 0.05808361 0.86617615]
# [0.60111501 0.70807258 0.02058449 0.96990985]
# [0.83244264 0.21233911 0.18182497 0.18340451]
# [0.30424224 0.52475643 0.43194502 0.29122914]]pd.DataFrame():将数组变成表格型数据结构
df=pd.DataFrame(a)
print(df) # 0 1 2 3
#0 0.374540 0.950714 0.731994 0.598658
#1 0.156019 0.155995 0.058084 0.866176
#2 0.601115 0.708073 0.020584 0.969910
#3 0.832443 0.212339 0.181825 0.183405
#4 0.304242 0.524756 0.431945 0.291229df.to_csv():存储为csv文件
df.to_csv('pd.csv')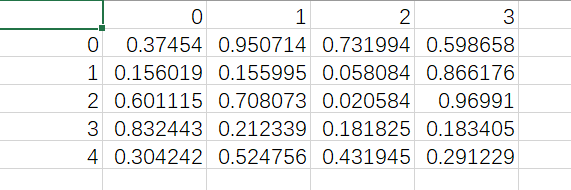
读取csv文件
data=pd.read_csv('pd.csv')
print(data)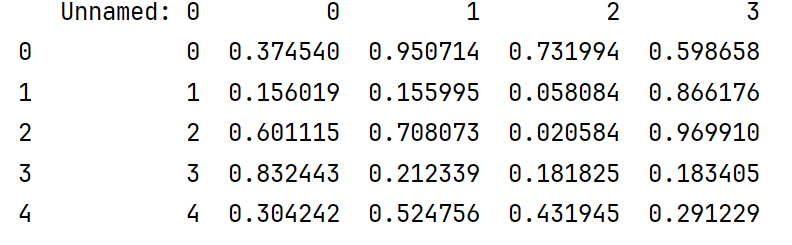




















 1969
1969

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








