数据结构和算法2 线性表的物理结构

1 线性表的定义

        线性表（List）：由零个或多个数据元素组成的有限序列。

        这里需要强调几个关键的地方： 首先它是一个序列，也就是说元素之间是有个先来后到的。 若元素存在多个，则第一个元素无前驱，而最后一个元素无后继，其他元素都有且只有一个前驱和后继。 另外，线性表强调是有限的，事实上无论计算机发展到多强大，它所处理的元素都是有限的。

       如果用数学语言来进行定义，可如下： 若将线性表记为（a1,…,ai-1,ai,ai+1,…an）,则表中ai-1领先于ai,ai领先于ai+1,称ai-1是ai的直接前驱元素,ai+1是ai的直接后继元素。 所以线性表元素的个数n(n>=0)定义为线性表的长度，当n=0时，称为空表。

       

2 数据类型

        数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。 例如很多编程语言的整型，浮点型，字符型这些指的就是数据类型

          在计算机中，内存也不是无限大的，你要计算入1+1=2这样的整型数字的加减乘除运算，显然不需要开辟很大的内存空间。 而如果要计算1.23456789+2.987654321这样带大量小数的，就需要开辟比较大的空间才存放的下。 于是计算机的研究者们就考虑，要对数据类型进行分类，分出多种数据类型来适合各种不同的计算条件差异。

          我们对已有的数据类型进行抽象，就有了抽象数据类型。 抽象数据类型（Abstract Data Type，ADT）是指一个数学模型及定义在该模型上的一组操作。 抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关。 比如1+1=2这样一个操作，在不同CPU的处理上可能不一样，但由于其定义的数学特性相同，所以在计算机编程者看来，它们都是相同的

         为了便于在之后的讲解中对抽象数据类型进行规范的描述，我们给出了描述抽象数据类型的标准格式：

        ADT 抽象数据类型名

        Data

                   数据元素之间逻辑关系的定义

       Operation

                   操作

       endADT

         抽象数据类型就是把数据类型和相关操作（相关操作又称为运算）捆绑在一起。

          数据结构的主要运算包括：建立create，消除destroy，从一个数据结构中删除delete一个数据元素，把一个数据元素插如insert到一个数据结构中，对一个数据结构进行访问access，对要给数据结构中的数据元素进行修改modify，对一个数据结构的数据元素进行排序sort，对要给数据结构中的数据元素进行查找search

3 线性表的抽象数据类型

    ADT 线性表（List）

    Data

            线性表的数据对象集合为｛a1,a2,a3,a4,...an｝,每个元素的类型均为DataType，其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除了最后一个元素an外，每一个元素有且只有一个直接后继元素，数据元素之间的关系是一对一的关系。

   Operation

            InitList（*L）:初始化操作，建立要给空的线性表L

            ListEmpty（L）：判断线性表是否为空表，若线性表为空，返回true，否则返回false

            ClearList（*L）：将线性表清空

            GetElem（L，i，*e）：将线性表L中的第i个位置元素值返回给e

            LocateElem（L,e）：在线性表L中查找与给定值e相等的元素，如果查找成功，返回该元素在表中的序号表示成功，否则，返回0表示失败

            ListInsert（*L，i，e）：在线性表L中第i个位置插入新元素e

            ListDelete（*l,i,*e）:删除线性表L中第i个位置元素，并用e返回其值

     endADT

4 线性表的顺序存储结构    

4.1   常规知识

           线性表有两种物理存储结构：顺序存储结构和链式存储结构。

           线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

           线性表（a1,a2,a3,...,an）的顺序存储如下：

           

             物理上的存储方式事实上就是在内存中找个初始地址，然后通过占位的形式，把一定的内存空间给占了，然后把相同数据类型的数据元素依次放在这块空地中

            接下来看一下线性表顺序存储的结构代码

#define MAXSIZE 20
typedef int ElemTyep;
typedef struct
{
	ElemTyep data[MAXSIZE];
	int length;
}SqList;

           大家可以看到，其就是对数组进行封装，同时增加了一个当前长度的变量

           总结：顺序存储结构封装需要三个属性：1、存储空间的起始位置，数组data，他的存储位置就是线性表存储空间的存储位置，即data数组第一个元素的存储地址就是该线性表的起始存储位置；2、线性表的最大存储容量：数组的长度MAXSIZE;3、线性表的当前长度length

           注意1：数组的长度和线性表的当前长度需要区分一下【数组的长度是存储线性表的存储空间的总长度，一般初始化后不变。而线性表的当前长度是线性表中元素的个数，是会变化的】

           注意2：线性表的计数从1开始

           注意3：假设ElemType占用的是c个存储单元（字节），那么线性表中第i+1个数据元素和第i个数据元素的存储位置的关系是【LOC(ai+1)=LOC(ai)+c】                                                                                  

           所以：对于第i个数据元素ai的存储位置可以由a1推算得出LOC(ai)=LOC(a1)+（i-1）*c

           

           注意4：通过上述公式，我们可以随时计算出线性表中任意位置的地址，不管他是第一个还是最后一个，都是相同的时间，那么他的存储时间性能当然就是O(1),我们通常称为随机存储结构

4.2 顺序存储的线性表的基本操作

        顺序存储的线性表中，很容易实现线性表的一些操作：初始化、赋值、查找、修改、插入、删除、求长度等

4.2.1 获取指定位置元素值

    实现GetElem的具体操作，即将线性表L中的第i个位置元素值返回，就程序而已，我们只需要把数组的i-1下标的值返回即可

#define ok 1
#define error 0

typedef int status;

status GetElem(SqList L, int i, ElemTyep *e)
{
	if (L.length == 0 || i<1 || i>L.length)
		return error;
	*e = L.data[i - 1];
	return ok;
}

             注意：上述代码返回值类型status是一个整型，约定返回1代表ok，返回0表示error，时间复杂度为o(1)

4.2.2、插入操作

              插入操作ListInsert（*L,i,e）,即在线性表L中的第i个位置插入新元素e

              插入算法的思路如下：如果插入位置不合理，抛出异常（或返回error状态）；如果线性表长度大于等于数组长度（即插入此元素后元素个数超出列表可以存放的元素最大值）则抛出异常或动态增加数组容量；从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置。将要插入元素填入位置i处【注意：位置i处在数组中下标为i-1】；线性表长度加1

status ListInsert(SqList *L, int i, ElemTyep e)
{
	/*step1:判断插入位置是否合理，不合理则直接返回*/
	if (i<1 || i>L->length+1)  //情况1：插入位置不合理，注意：可以在线性表尾部添加元素
		return error;
	if (L->length == MAXSIZE)  //情况2：线性表长度大于等于数组长度
		return error;
	/*step2:移动相应位置元素，将列表中下标为[i-1，length-1]之间所有元素向后移动*/
     if(i<=L->length)  //注意：i等于L->length+1时表示在表尾添加元素，此时无需移动元素
    {
	    for (int k = L->length-1;k >= i - 1;k--)  //情况3：插入位置在[1,length]之间
	    {
		    L->data[k+1] = L->data[k];
	    }
    }
	/*step3:将元素e插入线性表中下标为i-1的地方，同时线性表长度加一*/
	L->data[i - 1] = e;
	L->length++;
	return ok;
}

         分析时间复杂度如下：

         最好的情况：插入操作刚好要求在线性表尾部【例如一共有3个元素，此时下标最大为2，若要求在第4个位置处添加元素，则无需移动，直接data[3]=value即可】，此时无需移动元素，所以此时的时间复杂度为o(1)

         最坏的情况：如果插入操作的位置在第一个元素位置，那么就意味着要将所有元素都将后面移动一位，所以时间复杂度为O(n)

         平均的情况：取最好情况和最坏情况的中间值O（(n-1)/2）

         综上所述：插入操作的时间复杂度为O(n)

4.2.3 删除操作

            删除操作算法的思路：如何删除位置不合理，抛出异常；取出删除元素的元素值；从删除元素位置开始遍历到最后一个元素位置，分别将它们向前移动一个位置；表长减一

status ListDelte(SqList *L, int i, ElemTyep *e)
{
	/*step1:判断插入位置是否合理，不合理则直接返回*/
	if (i<1 || i>L->length)  //情况1：删除位置不合理
		return error;
	if (L->length == 0)      //情况2：线性表长度已经为0，没有可以删除的元素
		return error;
	/*step2:将被删位置i处元素值返回给e*/
	*e = L->data[i - 1];
	/*step3:移动相应位置元素，将列表中下标为[i，length-1]之间所有元素向前移动*/
	if (i < L->length)  //如果删除元素是最后一个，即i ==L.length，则不需要移动元素
	{
		for (int k = i;k >= L->length - 1;k++)  //情况3：删除元素位置在[1,length]之间
		{
			L->data[k - 1] = L->data[k];
		}
	}
	/*step4:线性表长度减一*/
	L->length--;
	return ok;
}

        分析时间复杂度如下：

         最好的情况：删除操作刚好要求在线性表最后一个元素【例如一共有3个元素，此时下标最大为2，若要求删除第三个元素，则无需移动，直接将线性表的长度减一即可】，此时无需移动元素，所以此时的时间复杂度为o(1)

         最坏的情况：如果删除操作的位置在第一个元素位置，那么就意味着要将所有元素都将向前移动一位，所以时间复杂度为O(n)

         平均的情况：取最好情况和最坏情况的中间值O（(n-1)/2）

         综上所述：删除操作的时间复杂度为O(n)

4.3 线性表顺序存储结构的优缺点

         线性表的顺序存储结构，在存【注意：存即是赋值】、读数据时，不管是哪个位置，时间复杂度都是O（1），而在插入或删除时，时间复杂度都是O(n)

         这就说明：它比较适合元素个数比较稳定，不经常插入和删除元素，而更多的是存取数据的应用

          线性表顺序存储结构的优点如下：

          1、无需为表示表中元素之间的逻辑关系而增加额外的存储空间；

          2、可以快速地存取表中任意位置的元素

          线性表顺序存储结构的缺点如下：

          1、插入和删除操作需要移动大量元素，此为最大缺点

          2、当线性表长度变化较大时，难以确定存储空间的容量

          3、容易造成存储空间的“碎片”

           上述讲的线性表的顺序存储结构，它最大的缺点就是插入和删除时需要移动大量元素，这显然就需要耗费时间。那我们能不能针对这个缺陷或者说遗憾提出解决的方法呢？要解决这个问题，我们就得考虑一下导致这个问题的原因。

            为什么当插入和删除时，就要移动大量的元素？原因就在于相邻两元素的存储位置也具有邻居关系，它们在内存中的位置是紧挨着的，中间没有间隙，当然就无法快速插入和删除

            解决方法就是：每个元素多用一个位置来存放指向下一个元素位置的指针，这样子从第一个元素就可以找到第二个元素，第二个元素可以找到第三个元素，以此类推，所有的元素我们就都可以通过遍历而找到，即线性表的链式存储即可解决这一缺陷

---

拓展知识1  结构体类型

                       https://www.cctry.com/thread-289320-1-1.html

                      1、自定义数据类型：
                      C/C++语言本身提供了很多基本数据类型，例如：int、float、char 等供我们使用。但是程序编写的过程中问题往往比较复杂，基本的数据类型有时候不能满足我们的需求，所以C/C++语言允许开发者根据自己的需要自定义数据类型，接下来要讲解的结构体struct、联合体union、枚举类型enum，类类型class 等就是用户自定义的数据类型。这些用户自定义的数据类型跟C/C++语言提供的基本类型一样，都可以用来定义变量。只不过在这些自定义数据类型在使用之前要先由用户声明出来才行。

                     2、定义结构体的必要性：
                    例如一个学生的信息包括：姓名，学号，性别，年龄 等等。按照我们之前的做法，可以使用数组来定义：

string name[100]; //姓名
int num[100]; //学号
char sex[100]; //性别
int age[100]; //年龄

                   这样虽然也能满足需求，但是比较麻烦，如果想获得一个学生的信息需要从4个数组中分别找到该学生的所有信息，而且没有什么关联性，容易乱，能不能把一个学生的信息都统一到一起呢？把他们当做一个组合项，在一个组合项中包含若干个类型的数据项。C/C++语言允许用户自己定义这样的数据类型，这样的类型就称作结构体。例如：

struct Student
{
    string name;
    int num;
    char sex;
    int age;
};

            这样就声明了一个结构体类型 Student，struct 是结构体类型的关键字，不能省略。

            3、结构体类型的声明：

struct 结构体类型名
{
    //成员表;
};

               struct 是声明该类型为结构体类型的关键字，不能省略。结构体类型名就是该结构体类型的名字，以后可以直接拿这个类型名来定义变量，就跟使用int，double一样用。类型名的命名规则跟变量一样，可以是数字、字母、下划线，且数字不能开头。上面例子中的 Student 就是结构体的类型名。接下来的一对大括号内的成员表包含了该结构体中的全部成员。上例中的 name、num、sex、age 都是结构体中的成员。在声明一个结构体类型时必须对各成员进行类型声明，即：
              类型名 成员名;
              例如：int num;
             备注：C语言中结构体的成员只能是数据，C++对此进行了扩充，结构体的成员既可以包含数据，也可以包含函数，其实在C++中 struct 跟 class 从使用角度来说差别不大！

            4、结构体类型变量的定义及初始化：
            A、定义：
          结构体类型声明完了之后就可以定义变量了，如：Student zhangsan, lisi;
          这种是非常常用的一种定义结构体类型变量的方法。当然也可以在声明结构体类型的时候就定义变量，当然这种是不常用的方法：

struct Student
{
    string name;
    int num;
    char sex;
    int age;
} zhangsan, lisi;

             B、初始化： Student zhangsan = {"张三", 1001, 'm', 25};
备注：初始化参数的顺序一定要和结构体类型声明的成员表顺序一致才行，不然会报错而且会错误的赋值。

           5、结构体类型变量成员的访问：
           结构体变量名.成员名

Student zhangsan = {"张三", 1001, 'm', 25};
zhangsan.num = 29;
int num = zhangsan.num;

拓展知识2    结构体声明时注意事项

                       

                 注意上述两段声明方式，左图使用typedef+struct来声明结构体，SqList是结构体类型名字，右图只是使用struct来声明结构体，lisi是结构体类型变量

拓展知识3  typedef和define具体的详细区别

                         https://www.cnblogs.com/rainbow70626/p/8809013.html

                         1) #define是预处理指令，在编译预处理时进行简单的替换，不作正确性检查，不关含义是否正确照样带入，只有在编译已被展开的源程序时才会发现可能的错误并报错。
                        2）typedef是在编译时处理的。它在自己的作用域内给一个已经存在的类型一个别名                                                                                           3）注意到#define 不是语句 不要在行末加分号，否则 会连分号一块置换。

---

5 线性表的链式存储结构（单链表）

          注意：线性表的链式存储结构包含：单链表、单循环链表、双向链表，双循环链表，本章主要介绍单链表，第六章主要介绍单循环链表，第七章注主要介绍双向链表，第八章介绍双循环链表

5.1 基础知识

            线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以存在内存中未被占用的任意位置

            存储链表中结点的任意一组的存储单元可以是连续的也可以是不连续的，甚至是零散分布在内存中的任意位置上，故链表中结点的逻辑顺序和物理顺序不一定相同

           比起顺序存储结构的每个数据元素只需要存储一个位置就可以了，现在的链式存储结构中，除了要存储数据元素信息外，还要存储它的后继元素的存储地址，称为指针pointer或链link

           也就是说除了存储其本身的信息外，还需存储一个指示其直接后继的存储位置的信息

           我们把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成的数据元素为存储映像，称为节点node

            n个节点链成一个链表，即为线性表（a1,a2,a3,...,an）

            因为此链表的每个节点中只包含一个指针域，所以叫做单链表

             

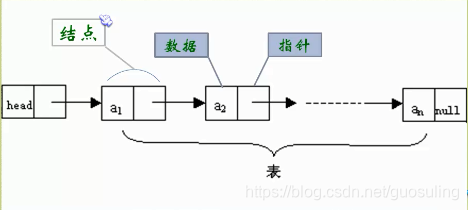
              对于线性表来说，总得有个头也有尾，链表也不例外，我们把链表中第一个结点的存储位置叫做头指针，最后一个结点指针为空null

            

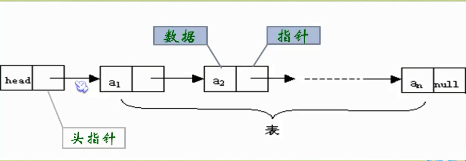
5.1.1 头指针和头结点的异同????????????? 

           头结点的数据域一般不存储任何信息。那么头指针和头结点有何异同呢？

           头指针：

           1、头指针是指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针

           2、头指针具有标识作用，所以常用头指针冠以链表的名字

           3、无论链表是否为空，头指针均不为空

           4、头指针是链表的必要元素

           头结点：

           1、头结点是为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义（但也可以存放链表的长度）

           2、有了头结点，对在第一个元素结点前插入结点和删除第一结点的操作与其他结点的操作就统一了

           3、头结点不一定是链表的必须要素

          单链表图例：

          

           空链表图例

           

5.1.2 单链表存储结构

typedef int ElemType;

typedef struct
{
	ElemType data;
	//struct node* next;  //注意此处：此语句和下一行语句意思一致，两种写法都可以
	node* next;
}node;

            我们可以看到结点由存放数据元素的数据域data和存放后继结点地址的指针域next组成。

            假设p是指向线性表第i个元素的指针，则该结点ai的数据域我们可以用p->data的值表示，结点ai的指针域可以用p->next来表示，p->next的值是一个指针，该指针指向的是第i+1个元素

            在线性表的顺序存储结构中，我们要计算任意一个元素的存储位置是很容易的。

            但是在单链表中，由于第i个元素到底在哪我们压根没办法一开始就知道，必须的从第一个结点开始挨个儿找

            因此，对于单链表实现获取第i个元素的数据的操作GetElem,在算法上相对要麻烦一点

5.2 单链表的基础操作

5.2.1 单链表的整表创建

          对于顺序存储结构的线性表的整表创建，我们可以用数组的初始化来直观理解

          而单链表和顺序存储结构就不一样了，它不像顺序存储结构这么集中，他的数据可以是分散在内存各个角落的，他的增长也是动态的

          对于每个链表来说，它所占用空间的大小和位置是不需要预先分配划定的，可以根据系统的情况和实际的需求即时生成

           创建单链表的过程是一个动态生成链表的过程，从空表的初始状态其，依次建立各元素结点并逐个插入链表

           所以单链表整表创建的算法思路如下：

           1、声明一结点p和计数器变量i；

           2、初始化一空链表L

           3、让L的头结点指针指向null，即建立一个带头结点的单链表

           4、循环实现后继结点的赋值和插入

           5、头插法从一个空表开始，生成新结点，读取数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到结束为止

简单来说，就是把新加进的元素放在表头的第一个位置：先让新结点的next指向头结点之后，然后让表头的next指向新结点

           6、尾插法就是将新结点都插入到最后。

          动态的建立单链表的常用方法有如下两种

           方法1：头插入法建表

           从一个空表开始，重复读入数据，生成新结点，将读入数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到读入结束标志为止，即每次插入的结点都作为链表的第一个结点。函数只需返回头结点即可。

LinkList  create_LinkList()
{
	/*step1：创建链表的头结点*/
	LinkList p, head;
	head = (LinkList)malloc(sizeof(node));
	head->next = NULL;
	/*step2:循环创建结点*/
	int data;
	while (1)
	{
		scanf("%d", &data);
		if (data == 32767)//注意：若int类型占用2个字节，2^16=32768
			break;
		p = (LinkList)malloc(sizeof(node));
		p->data = data;//为新结点的数据域赋值
		p->next = head->next;// 将新结点的成员指针next指向之前头结点指针指向的结点
		head->next = p;//将新结点接到头结点之后
	}
	return head;
}

         下为c++版本

#include<iostream>
using namespace std;
struct ListNode
{
	int data;
	ListNode * pnext;
};

ListNode * createList()
{
	//step1
	ListNode * cur = new ListNode;
	cur->data = 0;
	cur->pnext = NULL;
	//step2
	while (1)
	{
		int data;
		cin >> data;
		if (!data)
			break;
		ListNode * node = new ListNode;
		node->data=data;
		node->pnext = cur;
		cur = node;
	}
	//step3
	return cur;
}
int main()
{
	ListNode * head = createList();
	return 0;
}

 方法2 尾插入法建表

           头插入法建立链表虽然算法简单，但生成的链表中结点的次序和输入的顺序相反。若希望二者次序一致，可采用尾插法建表

           该法是将新结点插入到当前链表的表尾，使其成为当前链表的尾结点

LinkList  create_LinkList()
{
	/*step1：创建链表的头结点*/
	LinkList p, head, q;
	head = p = (LinkList)malloc(sizeof(node));
	p->next = NULL;
	/*step2:循环创建结点*/
	int data;
	while (1)
	{
		scanf("%d", &data);
		if (data == 32767)//注意：若int类型占用2个字节，2^16=32768
			break;
		q = (LinkList)malloc(sizeof(node));
		q->data = data;
		q->next = p->next;
		p->next = q;
		p = q;
	}
	return head;
}

       

ListNode * createList_back()
{
	ListNode * head = new ListNode;
	ListNode * cur = head;
	head->data = 0;
	head->pnext = NULL;
	while (1)
	{
		int data;
		cin >> data;
		if (!data)
			break;
		ListNode * node = new ListNode;
		node->data = data;
		node->pnext = NULL;
		cur->pnext = node;
		cur = node;
	}
	return head;
}

无论是哪种插入方法，如果要插入建立的单线性链表的结点是n个，算法的时间复杂度均为O(n)

       对于单链表，无论是哪种操作，只要涉及到钩链或重新钩链，如果没有明确给出直接后继，钩链或重新钩链的次序必须是先右后左

5.2.2 单链表的查找

          1、按序号查找，时间复杂度为O（n）

         对于单链表，不能像顺序表中那样直接按序号i访问结点，而只能从链表的头结点出发，沿链域next逐个结点往下搜索，直到搜索到第i个结点为止，因此，链表不是随机存取结构。

         获取链表第i个数据的算法思路如下：

         1、声明一个结点p指向链表第一个结点，初始化j从1开始，表示当前的p指向单链表的第一个结点

         2、当j<i时，就遍历链表，让p的指针向后移动，不断指向下一个结点，j++

         3、若在j还未等于i时，p指向的结点的指针域就等于空，那么说明第i 个元素不存在

         4、否则查找成功，返回p指向结点的数据

typedef int state;
#define ok 1
#define error 0

state GetElem(LinkList L, int i, ElemType *e)
{
	/*step1:初始化变量，使结点指针p指向头指针为L的单链表的第一个结点*/
	LinkList p;
	p = L->next;
	int j = 1;  //j表示此时结点指针p指向单链表的第几个元素
	/*step2:从第一个结点开始，遍历单链表，直至获得指向第i个结点的指针*/
	while (p&&j < i)
	{
		p = p->next;
		j++;
	}
	/*step3：判断此时指针p状态，若非法则返回error*/
	if (!p || j > i)  //！p表示指针为空，即已经到达最后一个结点；j>i表示此函数的输入i为小于1的值，此值非法
		return error;
	/*step4:此时指针p指向第i个结点，返回第i个元素的值*/
	*e = p->data;
	return ok;
}

     

int  GetItem(const ListNode * head, int index)
{
	//step1
	if (head == NULL || head->pnext == NULL||index<=0)
		return 0;
	//step2
	ListNode * cur = const_cast<ListNode *>(head);
	
	for (int i = 0;i <= index-1&&cur!=NULL;++i)
		cur = cur->pnext;
	//step3
	if (cur==NULL)
		return 0;
	return cur->data;
}

说白了，就是从头开始，直到找到指向第i个结点的指针位置，由于这个算法的时间复杂度取决于i的位置，当i=1时不需要遍历，而i=n时则遍历n-1次才可以，因此最坏情况的复杂度为O(n)

       由于单链表的结构中没有定义表长，岁不能事先知道要循环多少次，因此不方便使用for来控制循环

       其核心思想就是“工作指针后移”

       2、按值查找

        按值查找就是在链表中，查找是否有结点值等于给定值key的结点，若有，则返回首次找到的值为key的结点的存储位置，否则返回null，

        查找时从头结点出发，沿链表逐个将结点的值个给定值key做比较

LinkList Locate_node(LinkList L,ElemType e)
{
	/*step1:创建结点p，使其和L都指向头结点*/
	LinkList p = L;
	/*step2:遍历单链表，找到值就返回*/
	while (p)
	{
		if (p->data == e)
		{
			return p;
		}
		else
		{
			p = p->next;
		}
	}
	/*strp3:能执行到此步说明已经遍历到单链表的最后一个结点，故没有找到*/
	return NULL;
}

ListNode * GetItem_value(const ListNode * head, int value)
{
	//step1
	if (head == NULL || head->pnext == NULL)
		return NULL;
	//step2
	ListNode * cur = const_cast<ListNode *>(head);
	while (cur)
	{
		if (cur->data == value)
			return cur;
		cur = cur->pnext;
	}
	//step3
	return NULL;
}

---

拓展知识1    typedef struct node和struct node有什么区别

                             https://wenda.so.com/q/1474487914723293

                             typedef是类型定义的意思。typedef struct 是为了使用这个结构体方便

                            struct //是C中的结构体的关键词。 如： struct node{｝
                           node 相当于结构体的类型,关键是！其实在C中struct node 才相当于一个数据类型，如int ，所以在才会给初学者的带来困难，如在定一个变量时，要用 struct node xxx,而不是 node xxx 这就是关键。

                           而 typedef // 是自定义数据类型。
                           而且 typedef struct node {}A;
                           则是把 struct node 看做一个数据类型，不同的是这个结构体类型的定义也放在后面。 而A则是那个直观的数据类型名，引用的时候更加方便。

                          具体区别在于:
                          若struct node{ }这样来定义结构体的话。在定义 node 的结构体变量时，需要这样写:struct node n;若用typedef，可以这样写：typedef struct node{}NODE; 。在申请变量时就可以这样写：NODE n;其实就相当于 NODE 是node 的别名。区别就在于使用时，是否可以省去struct这个关键字。

---

5.2.3 单链表的插入

         

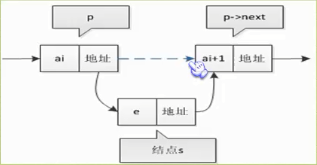
         单链表第i个数据处插入结点的算法如下：

          1、声明一结点p指向链表头结点，初始化j从1开始；

          2、当j<i时，就遍历链表，让p的指针向后移动，不断指向下一结点，j++

          3、若j<i时已经走到链表末尾则p指向的指针域为空，则说明第i个元素不存在

          4、否则查找成功，在系统中生成一个空结点s

          5、将数据元素e赋值给S->data

          6、单链表的插入：s->next=p->next,p->next=s

          下述代码中实现的功能是在第i个结点之后插入结点

//L为链表的头指针，其指针域指向头结点，头结点的指针域指向第一个结点
//此函数实现结果为：在链表的第i个结点之后插入新结点
state ListInsert(LinkList L, int i, ElemType e)
{
	/*step1:初始化变量，使结点指针p指向头指针为L的单链表的第一个结点*/
	LinkList p,s;    //s用于创建新结点
	p = L->next; //头指针的next内存放第一个结点的地址
	int j = 1;  //j表示此时结点指针p指向单链表的第几个元素
	/*step2:从第一个结点开始，遍历单链表，直至获得指向第i个结点的指针*/
	while (p&&j < i)
	{
		p = p->next;
		j++;
	}
	/*step3：判断此时指针p状态，若非法则返回error*/
	if (!p || j > i)  //！p表示指针为空，即已经到达最后一个结点；j>i表示此函数的输入i为小于1的值，此值非法
		return error;
	/*step4:此时指针p指向第i个结点，执行插入操作*/
	s = (LinkList)malloc(sizeof(node));
	s->data = e;  //数值域赋值
	s->next = p->next;  //新结点的指针域赋值，将当前链表中第i个元素接在新结点之后
	p->next = s;   //将新结点接在p结点之后，注意：此处的p结点是链表中第i-1个结点
	return ok;
}

         设链表的长度为n，合法的插入位置是1<=i<=n,算法的时间主要耗费在移动指针p上，故时间复杂度为O（n）

         若想在链表的第i个结点之前插入结点，则可按下述代码实现

//L为链表的头指针，其指针域指向头结点，头结点的指针域指向第一个结点
//此函数实现结果为：在链表的第i个结点之前插入新结点
state ListInsert(LinkList L, int i, ElemType e)
{
	/*step1:初始化变量，使结点指针p指向头指针为L的单链表的第一个结点*/
	LinkList p,s;    //s用于创建新结点
	p = L; //此时p是头指针，指向头结点
	int j = 0;  //j表示此时结点指针p指向单链表的第几个元素,j=0表示指向头结点
	/*step2:从第一个结点开始，遍历单链表，直至获得指向第i个结点的指针*/
	while (p&&j < i-1)  //此为找到第i个结点的前一个结点，即第i-1个结点
	{
		p = p->next;
		j++;
	}
	/*step3：判断此时指针p状态，若非法则返回error*/
	if (!p || j > i)  //！p表示指针为空，即已经到达最后一个结点；j>i表示此函数的输入i为小于1的值，此值非法
		return error;
	/*step4:此时指针p指向第i个结点，执行插入操作*/
	s = (LinkList)malloc(sizeof(node));
	s->data = e;  //数值域赋值
	s->next = p->next;  //新结点的指针域赋值，将当前链表中第i-1个元素接在新结点之后
	p->next = s;   //将新结点接在p结点之后，注意：此处的p结点是链表中第i个结点
	return ok;
}

int insertnode(ListNode * head, int index,int value)
{
	//step1
	if (head == NULL || index <= 0)
		return 0;
	//step2
	ListNode * cur = head;
	int i = 0;
	for (;i <= index-2&&cur;++i)
		cur = cur->pnext;
	//step3
	if (i==index-1&&cur != NULL)
	{
		ListNode * tmp = new ListNode;
		tmp->data = value;
		tmp->pnext = cur->pnext;
		cur->pnext = tmp;
		return 1;
	}
	return 0;
}

5.2.4 单链表的删除

         第一种删除：按序号删除

          

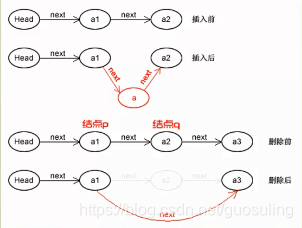
           假设元素a2的结点为q，要实现结点q的删除，其实就是将它的前继结点p的指针绕过结点q，直接指向结点q的后继结点即可。

            即：p->next=p->next->next

           单链表第i个数据删除结点的算法思路：

            1、声明结点p指向链表的头结点，初始化j=0

             2、当j<i-1时，就遍历链表，让p的指针向后移动，不断指向下一个结点，j++

             3、若p为空，则说明第i-1个元素不存在

            4、否则查找成功，将欲删除结点q->next赋值给p

            5、单链表的删除标准语句p->next=q->next

            6、将q结点中的数据赋值给e，作为返回

            7、释放q结点

state ListDelete(LinkList L, int i, ElemType *e)
{
	/*step1:初始化结点p，使其指向链表的头结点*/
	LinkList p,q;
	p = L; //此时p为头指针，指向头结点
	int j = 0; //j=0表示此时指针指向头结点
	/*step1:遍历链表，找到欲删除结点q的直接前继结点*/
	while (p&&j<i-1)
	{
		p = p->next;
		j++;
	}
	/*step3:判断是否找到前继结点*/
	if (!p || j > i)
		return error;
	/*step4:返回欲删除元素的值，执行删除结点操作,同时释放结点q*/
	//此时p结点指向欲删除结点q的前继结点
	q = p->next;
	*e = q->data;
	p->next = p->next->next;
	free(q);//注意：一定要在最后才释放q
	return ok;
}

       

int deletenode(ListNode * head, int index, int value)
{
//step1
	if (head == NULL || index <= 0)
		return 0;
	//step2
	ListNode * cur = head;
	int i = 0;
	for (;i <= index - 2 && cur != NULL;++i)
		cur = cur->pnext;
	//step3
	if (i == index - 1 && cur)
	{
		ListNode * tmp = cur->pnext;
		value = tmp->data;
		cur->pnext = tmp->pnext;
		delete tmp;
		return 1;
	}
	return 0;
}

 第二种删除：按值删除

        删除单链表中值为key的第一个结点

         与按值查找类似，首先要找到值为key的结点是否存在，若存在，就删除，否则返回error

state ListDelete_value(LinkList L,ElemType e)
{
	/*step1:创建结点p，使其和L都指向头结点*/
	LinkList p,q;
	p = L; //P指向头结点
	q = p->next;  //q指向p的下一结点，也就是第一个结点
	/*step2:遍历单链表，找到值就返回*/
	while (p&&q)  // 确保P和q均指向有效结点
	{
		//首先要保证q一定是p之后的一个结点指针，p是遍历单链表的指针
		if (q->data == e)//找到，删除
		{
			p->next = q->next;//删除q结点
			free(q);         //释放q指针
			return ok;        //返回
		}
		else//p指向下一个，继续遍历单链表
		{
			p = p->next;//p指向单链表的下一个结点
			q = p->next;//确保q一直是p的下一个结点
		}
	}
	/*strp3:能执行到此步说明已经遍历到单链表的最后一个结点，故没有找到*/
	return NULL;
}

   

int delenode(ListNode * head, int value)
{
	//step1
	if (head == NULL)
		return 0;
	//step2
	ListNode * cur = head;
	while (cur&&cur->pnext)
	{
		if (cur->pnext->data == value)
		{
			ListNode * tmp = cur->pnext;
			cur->pnext = tmp->pnext;
			delete tmp;
			return 1;
		}
		cur = cur->pnext;
	}
	return 0;

}

     变形删除算法1  删除单链表中值为key的所有结点

         与按值查找相类似，但比千米昂的算法更简单

         基本思想：从单链表的第一个结点开始，对每个结点进行检查，若结点的值为key，则删除，然后检查下一个结点，直到所有的结点都检查完。

int ListDelete_value_AllItem(LinkList L, ElemType e)
{
	/*step1:创建结点p，使其和L都指向头结点*/
	int num = 0;//初始化num，其记录一共找到几个指定值
	LinkList p, q;
	p = L;
	q = p->next;
	/*step2:遍历单链表，找到值就返回*/
	while (p&&q)
	{
		//首先要保证q一定是p之后的一个结点指针，p是遍历单链表的指针
		if (q->data == e)//找到，删除
		{
			p->next = q->next; //删除结点q
			free(q);  //释放q指向的结点，注意，此时q指向的是空的地址
			q = p->next; //重新为q赋值，以便进行下一次循环，注意：只要p变，q就一定要变，确保q指向是p指向的下一个结点
			num++;//注意：此处没有直接返回，故会遍历整个单链表
		}
		else//p指向下一个，继续遍历单链表
		{
			p = p->next;
			q = p->next;
		}
	}
	/*strp3:能执行到此步说明已经遍历到单链表的最后一个结点，返回删除个数num*/
	return num;
}

       

int delenode(ListNode * head, int value)
{
	//step1
	if (head == NULL)
		return 0;
	//step2
	int state = 0;
	ListNode * cur = head;
	while (cur&&cur->pnext)
	{
		if (cur->pnext->data == value)
		{
			ListNode * tmp = cur->pnext;
			cur->pnext = tmp->pnext;
			delete tmp;
			state = 1;
			continue;
		}
		cur = cur->pnext;
	}
	return state;

}

    变形删除算法2  删除单链表中所有值重复的结点，使得所有结点的值都不相同

            基本思想：从单链表的第一个结点开始，对每个结点进行检查，检查链表中该结点的所有后继结点，只要有值和该结点值相同，则删除；然后检查下一个结点，直到所有的结点都删除

int ListDelete_ALLvalue_NOTsame(LinkList L)
{
	/*step1:创建结点p，使其和L都指向头结点*/
	int num = 0;//初始化num，其记录一共找到几个指定值
	LinkList m, p, q;
	m = L->next;//m指向第一个结点，L指向头结点
	/*step2:遍历单链表，找到值就返回*/
	while(m)
	{ 
		p = m;
		q = p->next;
		while (p&&q)
		{
			//首先要保证q一定是p之后的一个结点指针，p是遍历单链表的指针
			if (q->data == m->data)//找到，删除
			{
				p->next = q->next;
				free(q);
				q = p->next;
				num++;//注意：此处没有直接返回，故会遍历整个单链表
			}
			else//p指向下一个，继续遍历单链表
			{
				p = p->next;
				q = p->next;
			}
		}
		m = m->next;
	}
	/*strp3:能执行到此步说明已经遍历到单链表的最后一个结点，返回删除个数num*/
	return num;
}

int delenode(ListNode * head)
{
	//step1
	if (head == NULL)
		return 0;
	//step2
	int state = 0;
	ListNode * cur = head;
	int value;
	while (cur&&cur->pnext)
	{
		value = cur->data;
		if (cur->pnext->data == value)
		{
			ListNode * tmp = cur->pnext;
			cur->pnext = tmp->pnext;
			delete tmp;
			state = 1;
			continue;
		}
		cur = cur->pnext;
	}
	return state;

}

 

5.2.5 单链表的整表删除

       当我们不打算使用这个单链表时，我们需要把它销毁；其实就是在内存中将它释放掉，以便留出空间给其他程序或软件使用

       单链表整表删除的算法思路如下：

        1、声明结点p和q

        2、将第一个结点赋值给p，下一个结点赋值给q

        3、循环执行释放p和将q赋值给p的操作

state ClearList(LinkList L)
{
	/*step1:定义结点指针p和q，将p和头指针L指向同处*/
	LinkList p, q;
	p = L;
	/*step2:获取p结点的下一个结点地址赋值给q，释放p，将q赋值给p*/
	while (p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	/*step3:头结点的指针域赋值为空，空链表就是链表的头结点的指针域为空*/
	L->next = NULL;
	return ok;
}

int deletelist(ListNode * head)
{
	//step1
	if (head == NULL)
		return 1;
	//step2
	ListNode * cur = head->pnext;
	ListNode * tmp;
	while (cur)
	{
		tmp = cur->pnext;
		delete cur;
		cur = tmp;
	}
	head->pnext = NULL;
	return 1;
}

5.2.6 单链表的合并

         设有两个有序（有序的意思是所有元素都是从小到大排列）的单链表，它们的头指针分别是La、Lb，将它们合并为以Lc为头指针的有序链表，合并前的示意图如下

         

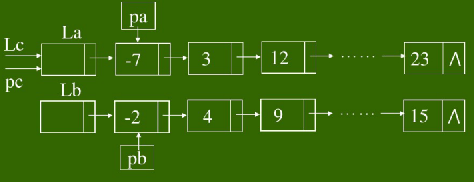
        合并后的结点示意图如下：

         

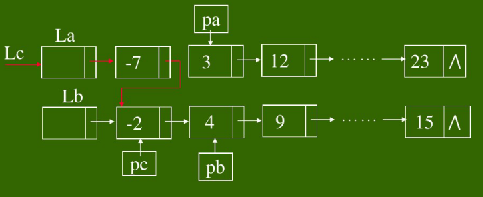
         算法说明：算法中pa、pb分别是待考察的两个链表的当前结点，pc是合并过程中合并的链表的最后一个结点

LinkList merge_linklist(LinkList la, LinkList lb)
{
	/*step1:初始化各单链表指针*/
	LinkList pa, pb, pc,head;
	pa = la->next;//pa指向单链表la的第一个结点,pa值为第一个结点的地址
	pb = lb->next;//pb指向单链表lb的第一个结点
	head = pc = la;//初始化合并后的头指针
	/*step2：比较pa和pb指向结点的值，链接到pc之后*/
	while (pa&&pb)//pa和pb单链表指向的内存不为空，则继续比较
	{
		if (pa->data <= pb->data)//pa指向的数据比pb指向的数据小
		{
			pc->next = pa;//pc链接pa
			pc = pc->next;//pc向后移动一个
			pa = pa->next;//pa向后移动一个
		}
		else
		{
			pc->next = pb;
			pc = pc->next;
			pb = pb->next;
		}
	}
	/*step3：若其中一个链表已经为空，则直接将另外一个链表链接在pc之后*/
	if (!pa&&pb)
	{
		pc->next = pb;
	}
	else if(!pb&&pa)
	{
		pc->next = pa;
	}
	/*step4:释放lb指针*/
	free(lb);
	return head;
}

   

ListNode * merge(ListNode * head1, ListNode * head2)
{
	//step1
	if (head1 == NULL)
		return head2;
	if (head2 == NULL)
		return head1;
	//step2
	ListNode * p1 = head1->pnext;
	ListNode * p2 = head2->pnext;
	ListNode * head;
	ListNode * tmp;
	if (p1->data <= p2->data)
		head = head1;
	else
		head = head2;
	tmp = head;
	while (p1&&p2)
	{
		if (p1->data <= p2->data)
		{
			tmp->pnext = p1;
			p1 = p1->pnext;

		}
		else
		{
			tmp->pnext = p2;
			p2 = p2->pnext;
		}
		tmp = tmp->pnext;
	}
	//step3
	if (p1)
		tmp->pnext = p1;
	if (p2)
		tmp->pnext = p2;
	//step4
	return head;
}

       上述代码时间复杂度为O（m+n）

           补充一个读取单链表所有结点元素的函数

state read_LinkList(LinkList L)
{
	LinkList p = L->next;//此时p指向单链表的第一个结点
	while (p)
	{
		printf("%d", p->data);
		p = p->next;
	}
	printf("\n");
	return ok;
}

5.2.7 效率pk

        我们最后的环节是效率pk，我们发现无论是单链表插入还是删除算法，它们其实都是由两个部分组成：第一部分就是遍历查找第i个元素，第二部分就是实现插入和删除元素

         从整个算法来说，我们很容易可以推出它们的时间复杂度都是O（n）

         故：如果我们不知道第i个元素的指针位置，单链表数据结构在插入和删除操作上，与线性表的顺序存储结构是没有太大优势的。 

         但如果，我们希望从第i个位置开始，插入连续10个元素，对于顺序存储结构意味着，每一次插入都需要移动n-i个位置，所以每次都是O（n）；而单链表，我们只需要在第一次时，找到第i个位置的指针，此时为O（n），接下来只是简单地通过赋值移动指针而已，时间复杂度都是O（1）

        显然，对于插入或删除数据越频繁的操作，单链表的效率优势就越明显了。

5.3 单链表结构域顺序存储结构的优缺点

         我们分别从存储分配方式，时间性能，空间性能三个方面来做对比

5.3.1 存储分配方式

          顺序存储结构用一段连续的存储单元依次存储线性表中的数据元素

          单链表采用链式存储结构，用一组任意的存储单元存储线性表的元素

5.3.2 时间性能

          1、查找

           顺序存储结构O（1），单链表O（n）

           2、插入和删除

            顺序存储结构需要平均移动表长一半的元素，时间为O（n）

            单链表在计算出某位置的指针后，插入和删除时间仅为O（1）

5.3.3、空间性能

            顺序存储结构需要预分配存储空间，分大了，容易造成空间浪费，分小了，容易发生溢出

            单链表不需要预先分配空间，只要有就可以动态分配，元素个数也不受限制

5.3.4 综上所述

            若线性表需要频繁查找，很少进行插入和删除操作，宜采用顺序存储结构

             若需要频繁插入和删除时，宜采用单链表结构

             比如游戏开发中，对于用户注册的个人信息，除了注册时插入数据外，绝大多数情况都是读取，所以应该考虑顺序存储结构

             而游戏中的玩家的武器或装备列表，随着玩家的游戏过程中，可能会随时增加或删除，此时再用顺序存储就不合适了，单链表结构就可以大展拳脚了

             当线性表中的元素个数变化较大或者根本不知道有多大时，最好用单链表结构，这样可以不需要考虑存储空间的大小问题

5.4 静态链表（此部分还未完成）

           c语言的指针的灵活性，使得它可以非常容易的操作内存中的地址和数据，这比其他高级语言更加灵活方便；

           早期没有c语言，没有java，只有原始的basic，fortran等早期的编程语言，这些语言没有类似于c的指针功能，但是它们又想描述单链表，就没法实现了，怎么办呢？有人想起了用数组代替指针来描述单链表

            这种用数组描述的链表叫做静态链表，这种描述方法叫做游标实现法

5.5 单链表小结腾讯面试题

         题目为：快速找到未知长度单链表的中间结点

5.5.1 普通方法

            首先遍历一遍单链表从而确定单链表的长度L，然后再次从头结点出发循环L/2次找到单链表的中间结点

            算法复杂度为O（L+L/2）=O(3L/2)

5.5.2 巧妙方法

            利用快慢指针。

             快慢指针的原理为：设置两个指针search和mid，初始化时都指向单链表的头结点。之后search移动速度是mid的2倍，当search到达尾结点时，mid指向中间结点。

//返回中间结点
LinkList mid_node(LinkList L,int *ser)
{
	/*step1:声明指针变量并进行初始化*/
	*ser = 0;
	LinkList search, mid;
	search = mid = L;//此时search和mid都指向第一个结点
	/*step2:遍历单链表*/
	while (search)
	{
		search = search->next;
		mid = mid->next;//mid指针每次循环向后移动一个
		(*ser)++;
		if(search) search = search->next;//search指针每次循环向后移动两个
	}
	return mid;
}

 

ListNode * middlenode(ListNode * head)
{
	//step1
	if (head == NULL|| head->pnext == NULL)
		return NULL;
	if (head->pnext->pnext == NULL)
		return head->pnext;
	//STEP2
	ListNode * slow = head->pnext;
	ListNode * fast = slow->pnext;
	while (slow&&fast)
	{
		slow = slow->pnext;
		fast = fast->pnext;
		if (fast)
			fast = fast->pnext;
	}
	//step3
	return slow;

}

---

拓展知识1 ：C语言的错误大全及中文解释：

                     https://wenda.so.com/q/1464238427726230

1: Ambiguous operators need parentheses — 不明确的运算需要用括号括起
2: Ambiguous symbol xxx — 不明确的符号
3: Argument list syntax error — 参数表语法错误
4: Array bounds missing — 丢失数组界限符
5: Array size toolarge — 数组尺寸太大
6: Bad character in paramenters — 参数中有不适当的字符
7: Bad file name format in include directive — 包含命令中文件名格式不正确
8: Bad ifdef directive synatax — 编译预处理ifdef有语法错
9: Bad undef directive syntax — 编译预处理undef有语法错
10: Bit field too large — 位字段太长
11: Call of non-function — 调用未定义的函数
12: Call to function with no prototype — 调用函数时没有函数的说明
13: Cannot modify a const object — 不允许修改常量对象
14: Case outside of switch — 漏掉了case 语句
15: Case syntax error — Case 语法错误
16: Code has no effect — 代码不可能执行到
17: Compound statement missing{ — 分程序漏掉"{"
18: Conflicting type modifiers — 不明确的类型说明符
19: Constant expression required — 要求常量表达式
20: Constant out of range in comparison — 在比较中常量超出范围
21: Conversion may lose significant digits — 转换时会丢失意义的数字
22: Conversion of near pointer not allowed — 不允许转换近指针
23: Could not find file xxx — 找不到XXX文件
24: Declaration missing ; — 说明缺少"；"
25: Declaration syntax error — 说明中出现语法错误
26: Default outside of switch — Default 出现在switch语句之外
27: Define directive needs an identifier — 定义编译预处理需要标识符
28: Division by zero — 用零作除数
29: Do statement must have while — Do-while语句中缺少while部分
30: Enum syntax error — 枚举类型语法错误
31: Enumeration constant syntax error — 枚举常数语法错误
32: Error directive :xxx — 错误的编译预处理命令
33: Error writing output file — 写输出文件错误
34: Expression syntax error — 表达式语法错误
35: Extra parameter in call — 调用时出现多余错误
36: File name too long — 文件名太长
37: Function call missing ) — 函数调用缺少右括号
38: Fuction definition out of place — 函数定义位置错误
39: Fuction should return a value — 函数必需返回一个值
40: Goto statement missing label — Goto语句没有标号
41: Hexadecimal or octal constant too large — 16进制或8进制常数太大
42: Illegal character x — 非法字符x
43: Illegal initialization — 非法的初始化
44: Illegal octal digit — 非法的8进制数字 A
45: Illegal pointer subtraction — 非法的指针相减
46: Illegal structure operation — 非法的结构体操作
47: Illegal use of floating point — 非法的浮点运算
48: Illegal use of pointer — 指针使用非法
49: Improper use of a typedefsymbol — 类型定义符号使用不恰当
50: In-line assembly not allowed — 不允许使用行间汇编
51: Incompatible storage class — 存储类别不相容
52: Incompatible type conversion — 不相容的类型转换
53: Incorrect number format — 错误的数据格式
54: Incorrect use of default — Default使用不当
55: Invalid indirection — 无效的间接运算
56: Invalid pointer addition — 指针相加无效
57: Irreducible expression tree — 无法执行的表达式运算
58: Lvalue required — 需要逻辑值0或非0值
59: Macro argument syntax error — 宏参数语法错误
60: Macro expansion too long — 宏的扩展以后太长
61: Mismatched number of parameters in definition — 定义中参数个数不匹配
62: Misplaced break — 此处不应出现break语句
63: Misplaced continue — 此处不应出现continue语句
64: Misplaced decimal point — 此处不应出现小数点
65: Misplaced elif directive — 不应编译预处理elif
66: Misplaced else — 此处不应出现else
67: Misplaced else directive — 此处不应出现编译预处理else
68: Misplaced endif directive — 此处不应出现编译预处理endif
69: Must be addressable — 必须是可以编址的
70: Must take address of memory location — 必须存储定位的地址
71: No declaration for function xxx — 没有函数xxx的说明
72: No stack — 缺少堆栈
73: No type information — 没有类型信息
74: Non-portable pointer assignment — 不可移动的指针（地址常数）赋值
75: Non-portable pointer comparison — 不可移动的指针（地址常数）比较
76: Non-portable pointer conversion — 不可移动的指针（地址常数）转换
77: Not a valid expression format type — 不合法的表达式格式
78: Not an allowed type — 不允许使用的类型
79: Numeric constant too large — 数值常太大
80: Out of memory — 内存不够用
81: Parameter xxx is never used — 能数xxx没有用到
82: Pointer required on left side of -> — 符号->的左边必须是指针
83: Possible use of xxx before definition — 在定义之前就使用了xxx（警告）
84: Possibly incorrect assignment — 赋值可能不正确
85: Redeclaration of xxx — 重复定义了xxx
86: Redefinition of xxx is not identical — xxx的两次定义不一致
87: Register allocation failure — 寄存器定址失败
88: Repeat count needs an lvalue — 重复计数需要逻辑值
89: Size of structure or array not known — 结构体或数给大小不确定
90: Statement missing ; — 语句后缺少"；"
91: Structure or union syntax error — 结构体或联合体语法错误
92: Structure size too large — 结构体尺寸太大
93: Sub scripting missing ] — 下标缺少右方括号
94: Superfluous & with function or array — 函数或数组中有多余的"&"
95: Suspicious pointer conversion — 可疑的指针转换
96: Symbol limit exceeded — 符号超限
97: Too few parameters in call — 函数调用时的实参少于函数的参数不
98: Too many default cases — Default太多(switch语句中一个)
99: Too many error or warning messages — 错误或警告信息太多
100: Too many type in declaration — 说明中类型太多
101: Too much auto memory in function — 函数用到的局部存储太多
102: Too much global data defined in file — 文件中全局数据太多
103: Two consecutive dots — 两个连续的句点
104: Type mismatch in parameter xxx — 参数xxx类型不匹配
105: Type mismatch in redeclaration of xxx — xxx重定义的类型不匹配
106: Unable to create output file xxx — 无法建立输出文件xxx
107: Unable to open include file xxx — 无法打开被包含的文件xxx
108: Unable to open input file xxx — 无法打开输入文件xxx
109: Undefined label xxx — 没有定义的标号xxx
110: Undefined structure xxx — 没有定义的结构xxx
111: Undefined symbol xxx — 没有定义的符号xxx
112: Unexpected end of file in comment started on line xxx — 从xxx行开始的注解尚未结束文件不能结束
113: Unexpected end of file in conditional started on line xxx — 从xxx 开始的条件语句尚未结束文件不能结束
114: Unknown assemble instruction — 未知的汇编结构
115: Unknown option — 未知的操作
116: Unknown preprocessor directive: xxx — 不认识的预处理命令xxx
117: Unreachable code — 无路可达的代码
118: Unterminated string or character constant — 字符串缺少引号
119: User break — 用户强行中断了程序
120: Void functions may not return a value — Void类型的函数不应有返回值
121: Wrong number of arguments — 调用函数的参数数目错
122: xxx not an argument — xxx不是参数
123: xxx not part of structure — xxx不是结构体的一部分
124: xxx statement missing ( — xxx语句缺少左括号
125: xxx statement missing ) — xxx语句缺少右括号
126: xxx statement missing ; — xxx缺少分号
127: xxx declared but never used — 说明了xxx但没有使用
128: xxx is assigned a value which is never used — 给xxx赋了值但未用过

---

6、循环链表（单循环链表）

6.1 基础知识

          循环，顾名思义就是绕。

          对于单链表，由于每个结点只存储了向后的指针，到了尾部标识就停止了向后继续链接的操作，也就是说，按照这样的方式，只能索引后继结点不能索引前驱结点。

          单链表会带来什么问题呢？例如不从头结点出发，就无法访问到全部结点，事实上要解决这个问题也并不麻烦，只需要将单链表中终端结点的指针端由空指针改为指向头结点。问题就解决了。

          将单链表中终端结点的指针由空结点改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表

         

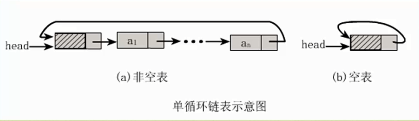
        注意：这里并不是说循环链表一定要有头结点

         其实循环链表和单链表的主要差异就在于循环的判断空链表的条件上，原来判断的结点指针尾null改为判断该结点是否指向头结点

        指向开始结点的指针为head，指向尾结点的指针为rear，故rear->next->next==head

         所以查找终端结点的时间复杂度为O（1），查找开始结点的时间复杂度为O（1）

6.2 循环链表的基础操作

        对于单循环链表 ，除链表的合并外，其他的操作和单线性链表基本一致，仅仅需要在单线性链表操作算法的基础上作以下简单修改

        判断是否是空链表：head->next==head

         判断是否是表尾结点：p->next==head

6.2.1 循环链表的初始化操作

          循环链表的初始化和单链表的初始化类似，区别在于循环链表无需头结点。

         以下代码以插尾法初始化循环链

CircularLinkList init()
{
	printf("开始创建单循环链表\n");
	/*step1:定义结点指针变量和存放输入数值的变量*/
	CircularLinkList head, p, q;
	int value = 0;//存放每次输入的结点数据域的值
	/*step2:创建第一个结点，注意：循环变量无需头结点*/
	head = (CircularLinkList)malloc(sizeof(node));//申请空间
	p = head;
	printf("请输入整型数字（注意：若输入-1，则表示链表创建结束）：value=");
	scanf("%d", &value);//输入数值域的数值
	p->data = value;//结点数值域赋值
	p->next = head;//结点指针域赋值
	p = p->next;//此时p指向第二个元素
	/*step3:创建循环链表的其他结点*/
	while (1)
	{
		printf("请输入整型数字（注意：若输入-1，则表示链表创建结束）：value=");
		scanf("%d",&value);
		if (value == -1)
		{
			printf("已经检测到终止数字-1\n");
			break;
		}
		q=(CircularLinkList)malloc(sizeof(node));
		q->data = value;
		q->next = p->next;
		p->next = q;
		p = q;
	}
	printf("创建单循环链表结束\n");
	printf("\n");
	return head;
}

6.2.2 读取单循环链表的全部元素值

      下述代码和之前读取单链表的元素函数相比，需要注意以下几点

         单循环链表没有头结点，指针L直接指向第一个有数字域的结点；

         判断读取到尾结点的条件是P->next!=L，读取指向指针尾结点时就退出了while，故最后一个结点的值没有输出，故许再加step3

state read_CircularLinkList(CircularLinkList L)
{
	printf("开始输出单循环链表的全部元素\n");
	/*step1：创建指针变量，使其和等于头指针*/
	CircularLinkList p = L;//此时L指向第一个结点（注意：循环链表没有头结点）
	/*step2:遍历链表，输出前n-1个元素*/
	while (p->next!=L)//注意：此循环结束时P->next==L，即p指向尾结点，此时循环会结束，故尾元素没有输出
	{
		printf("%d  ",p->data);
		p = p->next;
	}
	/*step3:此时p指向尾结点，直接输出其指向的尾结点的数值域*/
	printf("%d", p->data);
	printf("\n输出单循环链表元素结束\n");
	printf("\n");
	return ok;
}

6.2.3 向单循环链表中执行位置添加新结点

//向单循环链表的指定位置插入新结点
state insert_node(CircularLinkList * L,int i,ElemType value)
{
	printf("插入新结点开始\n");
	/*step1:声明并初始化各变量*/
	CircularLinkList p,q;
	p = *L;
	int j = 1;
	/*step2：若在链表第一个元素处插入结点，则需遍历找到最后一个结点*/
	if (i == 1)
	{
		printf("在第一个位置插入元素\n");
		while (p->next != *L)  p = p->next;
		q = (CircularLinkList)malloc(sizeof(node));
		q->data = value;
		p->next = q;
		q->next = *L;
		*L = q;
		printf("首位置插入结点结束\n\n");
		return ok;
	}
	/*step3:遍历单循环链表，找到指向第i个结点的指针*/
	while (p->next != *L&&j < i-1)
	{
		p = p->next;
		j++;
	}
	/*step4：判断错误情况，返回错误标志error*/
	if ((p->next == *L&&j < i) || j > i)
	{
		printf("位置错误：要求插入位置为%d，链表此时共有元素%d个,故未正确插入此结点\n\n",i,j);
		return error;//已经到尾结点，但此时还未找到指向第i个结点的指针;j>i此表示形参i为0
	}
		
	/*step5：插入新结点*/
	q = (CircularLinkList)malloc(sizeof(node));
	q->data = value;
	q->next = p->next;
	p->next = q;
	printf("在位置%d插入新结点(新结点元素值为%d)正确结束\n",i,value);
	printf("\n");
	return ok;		
}

            上述代码中需要注意的是：上述代码实现的功能为在结点i之前插入新结点。所以当形参i为1时（即在第一个元素之前插入一个新结点），需要找到最后一个结点，并将最后一个结点的指针域的指针指向新添加的结点

6.2.4 删除单循环链表指定位置的结点

state delete_node(CircularLinkList * L, int i)
{
	printf("删除指定位置处的结点\n");
	/*step1:声明指针变量并赋值*/
	CircularLinkList p,q;
	p = *L;
	int j = 1;
	/*step2：若要求删除首个结点*/
	if (i == 1)
	{
		while (p->next!= *L) p = p->next;
		p->next = (*L)->next;
		free(*L);
		*L = p->next;
		printf("删除链表首位置元素成功\n\n");
		return ok;
	}
	/*step3:删除除首个结点外的其他结点*/
	while (p->next != *L&&j < i - 1)
	{
		p = p->next;
		j++;
	}
	/*step4:判断指针p情况*/
	if (j > i || (j < i&&p->next == *L))
	{
		printf("位置错误：要求删除的结点序号为%d,链表包含结点个数为%d，故未正确删除\n\n",i,j);
		return error;
	}
	/*step5:删除指定结点*/
	q = p->next;
	p->next = q->next;
	printf("删除指定位置%d的元素值为%d的结点成功\n\n",i,q->data);
	free(q);
	return ok;

6.2.5 测试代码（main函数）

void main()
{
	/*step1:创建单循环链表*/
	CircularLinkList L = init();
	read_CircularLinkList(L);
	/*step2:测试3种情况下的插入操作*/
	insert_node(&L, 2, 5);
	read_CircularLinkList(L);
	insert_node(&L, 9, 5);
	read_CircularLinkList(L);
	insert_node(&L, 1, 8);
	read_CircularLinkList(L);
	/*step3:测试3种情况下的删除操作*/
	delete_node(&L, 1);
	read_CircularLinkList(L);
	delete_node(&L, 10);
	read_CircularLinkList(L);
	delete_node(&L, 6);
	read_CircularLinkList(L);
}

6.3  约瑟夫问题

            据说：著名犹太历史学家josephus讲过以下的故事：在罗马人占领桥塔帕特后，39个犹太人域josephus及他的朋友躲到一个洞中，39个犹太人决定宁死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第一个人开始报数，每报到第三人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止

             然而josephus和他的朋友并不像遵从，josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与31个位置，于是逃过了这场死亡游戏

             约瑟夫问题的41个人围成一个圈和我们的循环链表一样，我们可以让计算机模拟并告诉我们结果

             故问题：用循环链表模拟约瑟夫问题，把41个人自杀的顺序编号输出

6.3.1 约瑟夫问题正常解法

              1、若创建的单循环链表无头结点，则解决约瑟夫问题的函数如下：

//形参：L为无头结点的单循环链表，ser为数到几自杀
state solve_joseph(CircularLinkList L,int ser)
{
	CircularLinkList p, q, m;
	p = L;//此时p指向第一个结点
	while (p->next!= p)//此时创建的链表没有头结点，若p->next== p，表示只剩下一个元素
	{ 
        //首先找到需要删除的结点的直接前驱结点
		for (int i = 1;i < ser - 1;i++)//i表示此时p指向的结点报的数是几
		{
			p = p->next;	
		}
        //q指向要删除的结点	
		q = p->next;
	    printf("%d  ", q->data);
		p->next = q->next;
		free(q);
		p = p->next;
	}
    //将剩下的最后一个元素输出
	printf("%d",p->data);
	return ok;
}

         2、若创建的单循环链表有头结点，则解决约瑟夫问题的函数如下：

//形参L表示带有头结点的单循环链表，ser表示喊到几删除
state solve_joseph_with_headnode(CircularLinkList L, int ser)
{
	CircularLinkList p, q, m;
	p = L->next;//此时p指向第一个结点
	while (p->next != p)//若单循环链表带有头结点，故p->next == p时表示是空链表
	{
		//step1:while函数进来时一定要保证p指向的是喊1的元素
		if (p==L)//p=L表示此时p指向头结点，那么为了让p指向喊1的元素就必须时p向后走一位
		{
			p = p->next;
		}
		//step2:p遍历链表，要删除喊ser的元素，那么就要找到喊ser-1的元素
		for (int i = 1;i < ser - 1;i++)
		{
			p = p->next;
		}
		//step3:若p指向尾结点，则表示要删除的是第一个元素
		if (p->next == L)//p->next == L表示此时p指向尾结点
		{
			q = L->next;
			printf("%d ",q->data);
			L->next = q->next;
			free(q);
			p = p->next;
		}
		else//正常的删除结点
		{
			q = p->next;
			printf("%d ", q->data);
			p->next = q->next;
			free(q);
			p = p->next;
		}
	}
	return ok;
}

               注意：带不带头结点的单循环链表在解决约瑟夫问题时，重要的问题就是对于首结点的处理问题。头结点的问题有两点：第一点是：带有头结点的单链表在进入while时p不一定指向喊1的结点；第二个问题是当要删除的结点是首结点时会出现问题，其实，要删除首结点就是要删除第一个结点。

                注意：此处说的头结点是一般的头结点，即：数据域无实用信息的头结点。对于单循环链表来说，一般不设置这种头结点。

6.3.2 变形版本的约瑟夫问题

                编号为1-N的N的人按顺时针方向围坐一圈，每个人持有一个密码（正整数，可以自由输入），开始人选一个正整数作为报数上限M，从第一个人开始按顺时针方向自1开始顺序报数，报道M时停止报数。报M的人出列，将它的密码作为新的M值，从他的顺时针方向上的下一个人开始从1报数，如此下去，直至所有人全部出列为止。

              step1：定义新的结点的结构体类型，增加一个成员变量记录序号

typedef struct node 
{
	int ser;//存放序号
	int data;//存放密码
	node * next;//存放下一个结点指针
}node;

typedef struct node* LinkList;

              step2：定义初始化函数

//n表示链表中包含多少个结点，创建的链表没有头结点
LinkList init(int n)
{
	printf("开始创建包含%d个结点的单循环链表\n",n);
	LinkList head, p, q;
	head = (LinkList)malloc(sizeof(node));//创建头结点
	p = head;//当前指针指向头结点
	int password=0;
	for (int i=1;i<=n;i++)
	{
		printf("请输入第%d个人所持有的密码(注意：密码不能为1)：",i);
		scanf("%d",&password);
		q = (LinkList)malloc(sizeof(node));
		q->ser = i;
		q->data = password;
		p->next = q;
		p = q;
	}
	p->next = head->next;
	free(head);
	return p->next;
}

                step3：读取全部链表元素的函数（不是必须的，只是为了显式的看一下创建好的链表是否按预期所示）

typedef int state;
state read_LinkList(LinkList L)
{
	printf("开始读取L的全部元素\n");
	LinkList p = L;
	while (p->next!=L)
	{
		printf("%d(%d) ",p->ser,p->data);
		p = p->next;
	}
	printf("%d(%d) ", p->ser, p->data);
	printf("\n读取L的全部元素完毕\n\n\n");
	return 1;
}

          step4：解决约瑟夫问题

state solve_super_joseph(LinkList L)
{
	printf("解决约瑟夫问题中。。。。");
	/*step1:定义并初始化各变量*/
	LinkList p, q, m;
	p = L;
	int password = p->data;
	/*step2:解决问题*/
	while (p->next != p)//p->next == p表示只剩下一个元素
	{
		//首先查找要删除的结点的前驱结点
		for (int i = 1;i < password - 1;i++)
		{
			p = p->next;
		}
		q = p->next;
		password = q->data;//重新确定要删除的序号
		printf("%d ",q->ser);
		p->next = q->next;
		free(q);//释放已经删除的结点
		p = p->next;//确保p一直指向第一个结点
	}
	/*step3：最后要给元素*/
	printf("%d ",p->ser);
	printf("排序结束\n\n\n");
	return 1;
}

6.4 循环链表的特点

             回顾一下，在单链表中，我们有了头结点时，我们可以用O（1）的时间访问第一个结点，但对于要访问最后一个结点，我们必须要挨个向下索引，所以需要O（n）的时间

            我们表示循环链表一般只需要给出一个结点指针就可以，该结点指针指向第一个结点，但是这样的话我们要查找最后一个结点就需要O（n）的复杂度，但是我们修改一个这个结点指针的指向，使其指向尾结点，那么rear->next==head,故查找第一个结点和最后一个结点都只需要O（1）

            循环链表的特点就是无需增加存储量，仅对链接方式稍作改变，即可使得链表处理的更加方便灵活。

 6.4.1将两个单循环链表链接起来

                 题目：实现将两个线性表（a1,a2,a3,...,an）和(b1,b2,b3,...,bn)连接成一个线性表（a1,a2,a3...,an,b1,b2,b3,...,bn）的运算

                分析：

                 1、若在单链表或头指针表示的单循环表上做这种链接操作，都需要遍历第一个链表，找到结点a，然后将结点b1链到an的后面，其执行时间是O(n)

                 2、若在尾指针表示的单循环链表上实现，则只需修改指针，无需遍历，其执行时间是O（1）

                  

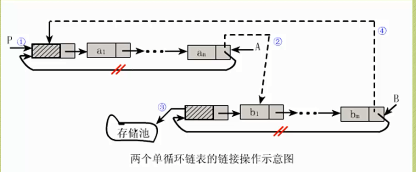
                 注意：下述代码中的La，和Lb是不包含无效的头结点的

//链接两个无头结点的单循环链表（无头结点的意思是没有值域无意义的结点）
CircularLinkList combine_a_b(CircularLinkList La, CircularLinkList Lb)
{
	//确定两个链表的头尾
	CircularLinkList rear_la = La;
	CircularLinkList head_la = rear_la->next;

	CircularLinkList rear_lb = Lb;
	CircularLinkList head_lb = rear_lb->next;
	//链接
	rear_la->next = head_lb;
	rear_lb->next = rear_la;

	return rear_la;
}

           注意：若单循环链表包含无效的头结点，那么需要注意下面两处地方

CircularLinkList combine_a_b(CircularLinkList La, CircularLinkList Lb)
{
	//确定两个链表的头尾
	CircularLinkList rear_la = La;
	CircularLinkList head_la = rear_la->next;

	CircularLinkList rear_lb = Lb;
	CircularLinkList head_lb = rear_lb->next;
	//链接
	rear_la->next = head_lb->next;//注意此处
	rear_lb->next = rear_la;
	free(head_lb);//注意此处

	return rear_la;
}

6.4.2 判断单链表中是否有环（未完成）

          有环的定义就是：链表的尾结点指向了链表中的某个结点。

          

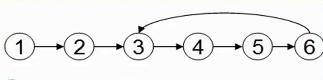
          那么要如何判断单链表中是否有环呢？主要有以下两种

           方法1：使用p，q两个指针，p总是向前走，但是q每次都是从头开始走，对于每个节点，看p走的步数是否和q一样，

           方法2：使用p，q两个指针，p每次向前走一步mq每次向前后两步，若在某一时刻，p==q，则存在环

6.4.3 魔术师发牌问题（未完成）

6.4.4 拉丁方阵问题（未完成）

7双向链表

7.1 基础知识

          双向链表（Double Linked List）：指的是构成链表的每个结点设立两个指针域，一个指向其直接前驱的指针域prior，一个指向其直接后继的指针域next。这样形成的链表中有两个方向不同的链，故称为双向链表

           单链表就是只有一个指针域，单链表的尾结点的指针域尾null。单循环链表就是尾结点的指针域指向头结点

           和单链表类似，双向链表一般增加头指针也能使双链表上的某些运算变得方便

          将头结点和尾结点链接起来也能构成循环链表，并称为双向循环链表

           双向链表是为了克服单链表的单向性的缺陷而引入的

          双向链表结点结构如下：

typedef struct node
{
	int data;
	node * prior;//前驱结点指针
	node * next;//后继结点指针
}node;
typedef  struct node* double_linklist;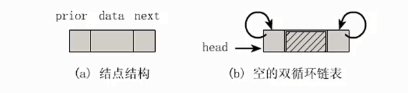

            

             既然单链表可以有循环链表，那么双向链表当然也可以有

           

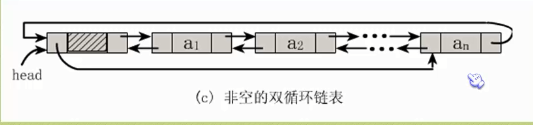
7.2 双向链表的基础操作

7.2.1 创建双向链表

            

//初始化双向链表
double_linklist init()
{
	printf("创建双向链表开始\n");
	/*step1:声明并初始化各变量，创建头结点*/
	int value = 0;
	double_linklist head, p, q;
	head = (double_linklist)malloc(sizeof(node));
	head->prior = NULL;
	head->next = NULL;
	p = head;
	/*step2:开始创建双向链表*/
	while (1)
	{
		//step2.1:首先获取结点元素值
		printf("请输入结点元素值（整型数据，输入-1表示创建链表结束）：");
		scanf("%d",&value);
		if (value == -1)
		{
			printf("检测到输入终止符-1，创建结束");
			break;
		}
		//step2.2 其次为新结点赋值
		q = (double_linklist)malloc(sizeof(node));
		q->data = value;
		q->prior = p;
		q->next = NULL;
		//step2.3 将新结点接到当前结点后面
		p->next = q;
		//step2.4 将当前结点后移一位
		p = q;
	}
	/*step3:创建结束*/
	printf("创建双向链表结束\n\n\n");
	return head;
}

7.2.2 双向链表的插入操作

           插入操作其实并不复杂，不过顺序很重要，千万不能写反

           

           

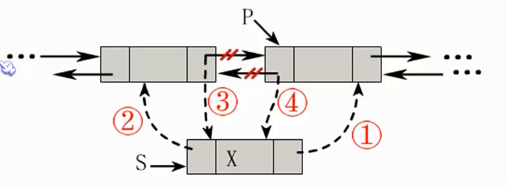
           插入顺序如下：

            1、先将新加入结点的后继指针域和前驱指针域依次赋值，即先将s插入到链表中

            2、为p结点的前驱结点的后继指针域赋值为s

            3、为p的前驱结点指针域赋值为s

//指定位置插入新结点
int insert_double_link(double_linklist *L,int ser,int value)
{
	printf("在指定位置%d插入结点元素值为%d的结点\n",ser,value);
	/*step1:定义并初始化各指针变量*/
	double_linklist p, q;
	p = *L;//此时p指向无实际意义的头结点
	int j = 0;//表示此时p指向第j个结点，头结点为0
	/*step2：找到指定结点*/
	while (p&&j<ser)
	{
		p = p->next;
		j++;
	}
	/*step3:判断此时p状态*/
	if (!p || j > ser)
	{
		printf("位置错误，此时双向链表共有结点%d个，要求插入的位置为%d，故插入失败\n\n\n",(j-1),ser);
		return 0;
	}
	/*step4:插入新结点*/
	q = (double_linklist)malloc(sizeof(node));
	q->data = value;
	q->prior = p->prior;
	q->next = p;
	p->prior->next = q;
	p->prior = q;
	printf("插入成功\n\n\n");
	return 1;
}

7.2.3 删除操作

            

            

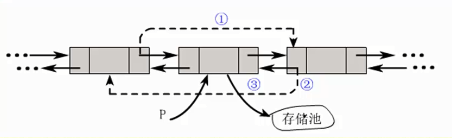
            双向链表可以有效提高算法的时间性能，其实就是空间换时间

int delete_double_link(double_linklist *L, int ser, int * value)
{
	printf("在指定位置删除结点\n");
	/*step1:定义并初始化各变量*/
	double_linklist p;
	p = *L;
	int j = 0;
	/*step2:遍历链表，找到指向指定位置的指针*/
	while (p&&j < ser)
	{
		p = p->next;
		j++;
	}
	/*step3:错误情况分析*/
	if (!p || j > ser)//p为空时
	{
		printf("指定位置错误，此时一共有%d个结点，但是要求删除的结点位置为%d，故删除操作失败\n\n\n",(j-1),ser);
		return 0;
	}
	/*step4:正常的删除操作*/
	p->prior->next = p->next;
	p->next->prior = p->prior;
	*value = p->data;
	free(p);
	printf("正确删除，在双向链表的位置%d，删除了元素值为%d的结点\n\n\n",ser,*value);
}

7.2.4 获取双向链表的全部元素

/输出双向链表的全部元素值
int read_double_linklist(double_linklist L)
{
	printf("开始输出双向链表的全部元素值\n");
	/*step1:定义当前指向的指针P，初始化为指向第一个结点*/
	double_linklist p = L->next;
	/*step2:遍历链表，输出元素值*/
	while (p)
	{
		printf("%d ",p->data);
		p = p->next;
	}
	/*step3:结束*/
	printf("\n输出结束\n\n\n");
	return 1;
}

7.2.5  测试上述代码的主函数

void main()
{
	/*创建双向链表*/
	double_linklist L = init();
	read_double_linklist(L);
	/*测试三种情况下的插入操作*/
	insert_double_link(&L, 2, 8);
	read_double_linklist(L);
	insert_double_link(&L, 1, 9);
	read_double_linklist(L);
	insert_double_link(&L, 9, 3);
	read_double_linklist(L);

	/*测试三种情况下的删除操作*/
	int value = 0;
	delete_double_link(&L, 3, &value);
	read_double_linklist(L);
	delete_double_link(&L, 1, &value);
	read_double_linklist(L);
	delete_double_link(&L, 9, &value);
	read_double_linklist(L);
}

                双向链表的整个cpp文件内容如下：

#include<iostream>
using namespace std;

typedef struct node
{
	int data;
	node * prior;//前驱结点指针
	node * next;//后继结点指针
}node;
typedef  struct node* double_linklist;

//初始化双向链表
double_linklist init()
{
	printf("创建双向链表开始\n");
	/*step1:声明并初始化各变量，创建头结点*/
	int value = 0;
	double_linklist head, p, q;
	head = (double_linklist)malloc(sizeof(node));
	head->prior = NULL;
	head->next = NULL;
	p = head;
	/*step2:开始创建双向链表*/
	while (1)
	{
		//step2.1:首先获取结点元素值
		printf("请输入结点元素值（整型数据，输入-1表示创建链表结束）：");
		scanf("%d",&value);
		if (value == -1)
		{
			printf("检测到输入终止符-1，创建结束");
			break;
		}
		//step2.2 其次为新结点赋值
		q = (double_linklist)malloc(sizeof(node));
		q->data = value;
		q->prior = p;
		q->next = NULL;
		//step2.3 将新结点接到当前结点后面
		p->next = q;
		//step2.4 将当前结点后移一位
		p = q;
	}
	/*step3:创建结束*/
	printf("创建双向链表结束\n\n\n");
	return head;
}

//输出双向链表的全部元素值
int read_double_linklist(double_linklist L)
{
	printf("开始输出双向链表的全部元素值\n");
	/*step1:定义当前指向的指针P，初始化为指向第一个结点*/
	double_linklist p = L->next;
	/*step2:遍历链表，输出元素值*/
	while (p)
	{
		printf("%d ",p->data);
		p = p->next;
	}
	/*step3:结束*/
	printf("\n输出结束\n\n\n");
	return 1;
}


//指定位置插入新结点
int insert_double_link(double_linklist *L,int ser,int value)
{
	printf("在指定位置%d插入结点元素值为%d的结点\n",ser,value);
	/*step1:定义并初始化各指针变量*/
	double_linklist p, q;
	p = *L;//此时p指向无实际意义的头结点
	int j = 0;//表示此时p指向第j个结点，头结点为0
	/*step2：找到指定结点*/
	while (p&&j<ser)
	{
		p = p->next;
		j++;
	}
	/*step3:判断此时p状态*/
	if (!p || j > ser)
	{
		printf("位置错误，此时双向链表共有结点%d个，要求插入的位置为%d，故插入失败\n\n\n",(j-1),ser);
		return 0;
	}
	/*step4:插入新结点*/
	q = (double_linklist)malloc(sizeof(node));
	q->data = value;
	q->prior = p->prior;
	q->next = p;
	p->prior->next = q;
	p->prior = q;
	printf("插入成功\n\n\n");
	return 1;
}


int delete_double_link(double_linklist *L, int ser, int * value)
{
	printf("在指定位置删除结点\n");
	/*step1:定义并初始化各变量*/
	double_linklist p;
	p = *L;
	int j = 0;
	/*step2:遍历链表，找到指向指定位置的指针*/
	while (p&&j < ser)
	{
		p = p->next;
		j++;
	}
	/*step3:错误情况分析*/
	if (!p || j > ser)//p为空时
	{
		printf("指定位置错误，此时一共有%d个结点，但是要求删除的结点位置为%d，故删除操作失败\n\n\n",(j-1),ser);
		return 0;
	}
	/*step4:正常的删除操作*/
	p->prior->next = p->next;
	p->next->prior = p->prior;
	*value = p->data;
	free(p);
	printf("正确删除，在双向链表的位置%d，删除了元素值为%d的结点\n\n\n",ser,*value);
}


void main()
{
	/*创建双向链表*/
	double_linklist L = init();
	read_double_linklist(L);
	/*测试三种情况下的插入操作*/
	insert_double_link(&L, 2, 8);
	read_double_linklist(L);
	insert_double_link(&L, 1, 9);
	read_double_linklist(L);
	insert_double_link(&L, 9, 3);
	read_double_linklist(L);

	/*测试三种情况下的删除操作*/
	int value = 0;
	delete_double_link(&L, 3, &value);
	read_double_linklist(L);
	delete_double_link(&L, 1, &value);
	read_double_linklist(L);
	delete_double_link(&L, 9, &value);
	read_double_linklist(L);
}

8、双向循环链表

8.1  基础知识

            首先对比一下单链表和单循环链表，双向链表和双向循环链表的操作区别

            初始化方面：

           1、单链表和双向链表的初始化都需要头结点，此时头指针指向头结点，头结点的数值域无需赋值，头结点的指针域（双向循环链表包含两个指针域）赋值为空NULL；创建其他结点时，结点的指针域都为NULL。

           2、单循环链表的双向循环链表都不需要头结点，头指针指向第一个结点，第一个结点的数值域即为第一个元素值，第一个结点的指针域（双向循环链表包含两个指针域）赋值为头指针；创建其他结点时，结点的next指针域都赋值为头指针；【对于双向循环链表，还需要在最后将头结点的prior赋值为尾结点】

           指定位置插入元素方面：

           1、单链表和双向链表的所有插入位置操作相同

           2、单循环链表的插入位置分为两种：插入到第一个元素处（因为要插入到第一个元素处，需要找到最后一个结点的地址；插入到第一个元素处，那么头指针指向的头结点的指针域也要改变），插入到非第一个元素处

           3、双循环链表的插入位置分为两种：插入到第一个元素处（插入到第一个元素处，那么头指针指向的头结点的指针域也要改变），插入到非第一个元素处。

            删除指定位置元素方面：

           1、单链表和双向链表的所有删除位置操作基本相同（单链表找到第i-1个结点，双向链表找到第i个结点）

           2、单循环链表的删除位置分为两种：删除到第一个元素处（删除要插入到第一个元素处，需要找到最后一个结点的地址；删除到第一个元素处，那么头指针指向的头结点的指针域也要改变），删除到非第一个元素处。

                 同时单循环链表遍历链表的条件和单链表不同，虽然都是遍历到指向尾结点结束，但是单链表具体条件为P！=NULL,而单循环链表的具体条件为P->next！=（*L）

           3、双循环链表的删除位置分为两种：删除到第一个元素处（删除到第一个元素处，那么头指针指向的头结点的指针域也要改变），删除到非第一个元素处。

              双向链表和双向循环链表遍历终止条件和单链表单循环链表类似。

              注意：删除和插入操作的非法位置可以全部改为（j!=i）

8.2   双向循环链表基本操作

8.2.1 初始化操作

//初始化双向循环链表
double_cir_linklist init()
{
	printf("创建双向循环链表开始\n");
	/*step1:声明并初始化各变量，创建头结点*/
	int value = 0;
	double_cir_linklist head, p, q;
	head = (double_cir_linklist)malloc(sizeof(node));
	printf("请输入结点元素值（整型数据）：");
	scanf("%d", &value);
	head->data = value;
	head->prior = head;
	head->next = head;
	p = head;
	/*step2:开始创建双向链表*/
	while (1)
	{
		//step2.1:首先获取结点元素值
		printf("请输入结点元素值（整型数据，输入-1表示创建链表结束）：");
		scanf("%d", &value);
		if (value == -1)
		{
			printf("检测到输入终止符-1，创建结束");
			break;
		}
		//step2.2 其次为新结点赋值
		q = (double_cir_linklist)malloc(sizeof(node));
		q->data = value;
		q->prior = p;
		q->next = head;
		//step2.3 将新结点接到当前结点后面
		p->next = q;
		//step2.4 将当前结点后移一位
		p = q;
	}
	head->prior = p;//将第一个结点的前驱结点链接到最后一个
	/*step3:创建结束*/
	printf("创建双向链表结束\n\n\n");
	return head;
}

8.2.2  插入操作

//指定位置插入新结点
int insert_double_cir_link(double_cir_linklist *L, int ser, int value)
{
	printf("在指定位置%d插入结点元素值为%d的结点\n", ser, value);
	/*step1:定义并初始化各指针变量*/
	double_cir_linklist p, q;
	p = *L;//此时p指向无实际意义的头结点
	int j = 1;//表示此时p指向第j个结点，头结点为0
	 /*step2：找到指定结点*/
	while (p->next!=(*L)&&j<ser)
	{
		p = p->next;
		j++;
	}
	/*step3:判断此时p状态*/
	if (j!=ser)
	{
		printf("位置错误，此时双向链表共有结点%d个，要求插入的位置为%d，故插入失败\n\n\n", j, ser);
		return 0;
	}
	/*step4:插入新结点*/
	q = (double_cir_linklist)malloc(sizeof(node));
	q->data = value;
	q->prior = p->prior;
	q->next = p;
	p->prior->next = q;
	p->prior = q;
	printf("插入成功\n\n\n");
	/*step5:如果插入的是第一个位置，则返回的头指针要改变*/
	if (ser==1)
	{
		(*L) = q;
	}
	return 1;
}

8.2.3 删除操作

//指定位置删除结点
int delete_double_cir_link(double_cir_linklist *L, int ser, int * value)
{
	printf("在指定位置删除结点\n");
	/*step1:定义并初始化各变量*/
	double_cir_linklist p, q;
	p = *L;
	int j = 1;
	/*step2:遍历链表，找到指向指定位置的指针*/
	while (p!=(*L)->prior&&j < ser)
	{
		p = p->next;
		j++;
	}
	/*step3:错误情况分析*/
	if (j!=ser)//p为空时
	{
		printf("指定位置错误，此时一共有%d个结点，但是要求删除的结点位置为%d，故删除操作失败\n\n\n", j, ser);
		return 0;
	}
	/*step4:正常的删除操作*/
	p->prior->next = p->next;
	p->next->prior = p->prior;
	*value = p->data;
	/*step5:如果删除的位置是1，则头指针指向改变*/
	if (ser==1)
	{
		(*L) = (*L)->next;
	}
	free(p);
	printf("正确删除，在双向链表的位置%d，删除了元素值为%d的结点\n\n\n", ser, *value);
}

8.2.4 读取双向循环链表的全部元素值

//输出双向链表的全部元素值
int read_double_cir_linklist(double_cir_linklist L)
{
	printf("开始输出双向链表的全部元素值\n");
	/*step1:定义当前指向的指针P，初始化为指向第一个结点*/
	double_cir_linklist p = L;
	/*step2:遍历链表，输出元素值*/
	while (p->next!=L)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	/*step3:结束*/
	printf("%d",p->data);
	printf("\n输出结束\n\n\n");
	return 1;
}

8.2.5 测试的main函数

void main()
{
	/*创建双向链表*/
	double_cir_linklist L = init();
	read_double_cir_linklist(L);
	/*测试三种情况下的插入操作*/
	insert_double_cir_link(&L, 2, 8);
	read_double_cir_linklist(L);
	insert_double_cir_link(&L, 1, 9);
	read_double_cir_linklist(L);
	insert_double_cir_link(&L, 9, 3);
	read_double_cir_linklist(L);

	/*测试三种情况下的删除操作*/
	int value = 0;
	delete_double_cir_link(&L, 3, &value);
	read_double_cir_linklist(L);
	delete_double_cir_link(&L, 1, &value);
	read_double_cir_linklist(L);
	delete_double_cir_link(&L, 9, &value);
	read_double_cir_linklist(L);
}

8.3 双向循环链表实践（未完成）

           题目：要求实现用户输入一个数使得26个字母的排列顺序发生变化。例如输入3，输出结果：DEF.....ABC;如果输入-3，输出结果XYZABC....UVW

            题目：维吉尼亚加密：当输入明文，自动生成随机密钥匹配明文中每个字母并移位加密

            题目：一元多项式的表示和相加

 

参考：小甲鱼