机器学习算法：朴素贝叶斯法

• 基于贝叶斯定义和特征条件独立假设的分类方法
• 对给定数据集，先学习输入输出的联合分布，再基于此模型，对给定的x利用贝叶斯定理求后验概率最大的输出y
• 实现简单，学习和预测的效率高

朴素贝叶斯法的学习与分类

基本方法

• 输入空间为  的n维度向量集合，输出空间为 标记集合 y = 
• 输入为特征向量 ，输出为类标记  
• X 是定义在输入空间 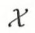 的随机变量，Y 是定义在 输出空间  的随机变量
•  是 X 和 Y 的联合概率分布
• 训练数据集  由  独立同分布产生

朴素贝叶斯法通过训练集学习联合分布  ，包括：

1. 先验概率分布： 
2. 条件概率分布：

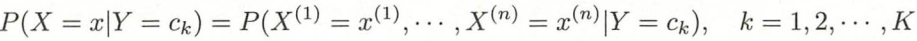
以此得到联合分布：

 

条件概率分布

 有指数级数量参数，设  可取值有  ， 可取值有  ，参数有 ，，估计实际不可行

朴素贝叶斯对条件概率分布做了条件独立性假设。这个假设对分布做了很强的限制，所以算法以此得名

条件独立性假设：

此假设说明在分类Y 确定的情况下，每个特征都是独立的。该假设简化了模型，但有时损失了准确率

因为学习得到的是，不是直接得到P( Y | X)，所以朴素贝叶斯是生成模型。机器学习“判定模型”和“生成模型”有什么区别

 

后验概率分布计算

根据贝叶斯定理：

代入条件独立性假设，有： 

这就是想要的后验概率分布，将后验概率最大的y作为x 的类输出：

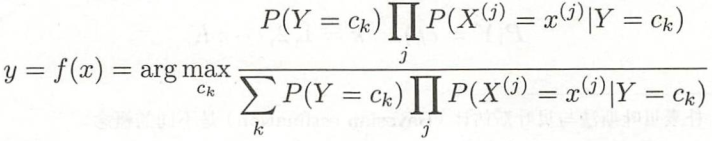
上式所有ck相同，所以 ：

 

后验概率最大化含义

假设用0-1损失函数： 

 为分类决策函数，此时期望风险函数为： 

是关于联合分布  的期望，则等价为： （这里是将外层的期望E 看做Exy，然后对y的期望放到右侧）

为使上式最小化，需要对每个  极小化， 得到：

于是这里期望风险最小化就等价于后验概率最大化，这就是朴素贝叶斯的原理

 

朴素贝叶斯法的参数估计

极大似然估计

朴素贝叶斯要学习的过程是估计先验概率： 和条件概率：  ，可用极大似然估计法

先验概率  的极大似然估计：

设第 j 个特征 可能的取值集合为： ，条件概率  的极大似然估计是：

 是第i个样本的第j个特征， 是第j个特征的可能取的第l个值， 为指示函数

 

学习与分类算法

输入

训练数据  

其中  ， 是第i个样本的第j个特征。 ， 是第j个特诊更可能取到的第l个值。

实例x。

输出

实例x的分类

1. 计算先验概率和条件概率： 
   
    
2. 对于给定实例 ，计算 
   
3. 确定实例x的类
   

贝叶斯估计

极大似然可能会遇到概率为0的情况，导致后验概率分母为0，解决方法是采用贝叶斯估计：

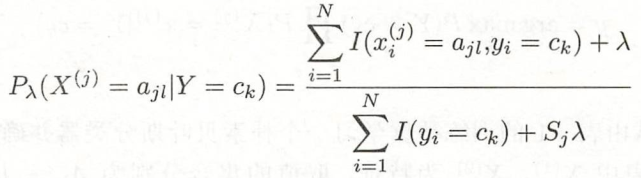
，等价于在每个类别取值频数上加一个，当=0则是极大似然估计。常取  = 1，成为拉普拉斯平滑。

对任何  有：

同样，先验概率的贝叶斯估计为：

 

练习

章末公式推导

 

参考：

《统计学习方法》

《深入浅出python机器学习》

请用简单易懂的语言描述朴素贝叶斯分类器？

聊一聊机器学习的MLE和MAP：最大似然估计和最大后验估计

带你搞懂朴素贝叶斯分类算法

深入理解朴素贝叶斯（Naive Bayes）

朴素贝叶斯算法原理小结

逻辑回归与朴素贝叶斯有什么区别？