Dijkstra算法是用来解决单元最短路径的一种算法。在一个加权的图中,给定一个源点,可以使用Dijkstra算法求这个顶点到其它各个顶点的最短路径。
Dijkstra算法是一个典型的贪心算法,每一步确定一个顶点到源点的最短路径。算法开始的时候,我们可以假定所有的顶点到源的距离d均未知(可以设置这些顶点到源点的距离为一个指定的最大值),我们可以将这些顶点组成的集合成为未知顶点集;显然,源点距离源点自身的距离可以认为是0。之后我们使用一个循环,每次循环,我们查看当前位置顶点集中,到源点具有最小距离的顶点,这个距离,为源点到该点所有可达的路径中,具有最小距离的路径,这样我们就确定了该顶点到源的距离;之后我们将该顶点从未知顶点集中删除,加入到已知顶点集中(实际上代码中并不需要将该顶点添加到已知顶点集,此处只是为了叙述方便)同时更新该顶点的邻接表中的顶点的距离,如果通过该顶点到达邻接表中的结点,具有更短的距离,则将邻接表中的顶点的距离更新为新的值。最终,未知顶点集为空(这个终止条件只适用于连通图,并且源到所有结点均可达),循环结束。
Distra算法每次的结点选择使用的是贪心策略,每次选取的的顶点,是当前未知顶点集中到源点距离最小的顶点。由于这个距离是当前源通过所有已知顶点集中的能够到达的所有未知顶点集中最小的值,不可能寻找到一个更短的路径使这个距离的值变小,所以可以确定这个顶点到源点的最短距离(但是其他未知顶点的距离,是有机会通过该顶点变得更小的)。
图的表示通常可以采用邻接矩阵和邻接表法,对于顶点之间连接比较稀疏的图,通常邻接矩阵会浪费更多的存储空间,因此本例中使用邻接表来存储图中顶点之间的连线。
一个可能的表示顶点的结构体:
struct vertex
{
unsigned int distance; //顶点到源点的距离
vertex* preV; //当前的距离所对应的路径上,本顶点的下一个顶点
map<vertex*, unsigned int> adjs; //用来存储本顶点的邻接顶点,key为顶点,value为权重(此处权重非负)
vertex()
{
distance = MAX_DISTANCE; //初始时所有顶点到源点的距离均为无穷大
preV = nullptr;
}
};
一个完整的例子如下(参考《数据结构与算法分析C++描述第三版》):
图:
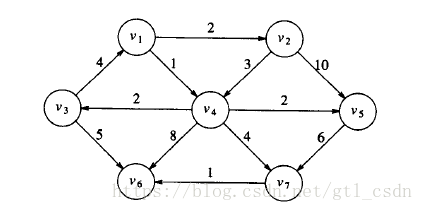
代码:
#include <iostream>
#include <map>
#include <vector>
using namespace std;
const int MAX_DISTANCE = 100000;
struct vertex
{
unsigned int distance;
vertex* preV;
map<vertex*, unsigned int> adjs;
vertex()
{
distance = MAX_DISTANCE;
preV = nullptr;
}
};
void loadVertexs(vector<vertex*>& vertexs)
{
vertex* v1 = new vertex();
vertex* v2 = new vertex();
vertex* v3 = new vertex();
vertex* v4 = new vertex();
vertex* v5 = new vertex();
vertex* v6 = new vertex();
vertex* v7 = new vertex();
map<vertex*, unsigned int> v1adj;
v1adj[v2] = 2;
v1adj[v4] = 1;
map<vertex*, unsigned int> v2adj;
v2adj[v4] = 3;
v2adj[v5] = 10;
map<vertex*, unsigned int> v3adj;
v3adj[v1] = 4;
v3adj[v6] = 5;
map<vertex*, unsigned int> v4adj;
v4adj[v3] = 2;
v4adj[v5] = 2;
v4adj[v6] = 8;
v4adj[v7] = 4;
map<vertex*, unsigned int> v5adj;
v5adj[v7] = 6;
map<vertex*, unsigned int> v6adj;
map<vertex*, unsigned int> v7adj;
v7adj[v6] = 1;
v1->adjs = v1adj;
v2->adjs = v2adj;
v3->adjs = v3adj;
v4->adjs = v4adj;
v5->adjs = v5adj;
v6->adjs = v6adj;
v7->adjs = v7adj;
vertexs.push_back(v1);
vertexs.push_back(v2);
vertexs.push_back(v3);
vertexs.push_back(v4);
vertexs.push_back(v5);
vertexs.push_back(v6);
vertexs.push_back(v7);
}
void processVertexs(const vector<vertex* >& vertexs)
{
vector<vertex*> tmp = vertexs;
tmp[0]->distance = 0;
//这个终止条件仅限于源点到所有顶点均可达的情况
while (tmp.size() > 0)
{
unsigned int shortDistance = MAX_DISTANCE;
unsigned int index = 0;
//查找未知顶点集中,距源点距离最小的点
for (unsigned int i = 0; i < tmp.size(); i++)
{
if (tmp[i]->distance < shortDistance)
{
index = i;
shortDistance = tmp[i]->distance;
}
}
//更新找到的点的邻接表中顶点到源点的距离
//由于仅在此时才会更新顶点的距离,一个改进的办法是,记录当前的最短距离的顶点和距离,
//更新邻接表的顶点的距离时,同时更新最短距离的顶点和距离,这样可以省去上面的循环。
//当图比较大,但是图中顶点的连接比较稀疏时,可以明显加快速度
for (auto it = tmp[index]->adjs.begin();
it != tmp[index]->adjs.end(); it++)
{
if (it->second + tmp[index]->distance < it->first->distance)
{
it->first->distance = it->second + tmp[index]->distance;
it->first->preV = tmp[index];
}
}
//remove this vertex
tmp.erase(tmp.begin() + index);
}
}
void printVertexs(const vector<vertex*>& vertexs)
{
for (unsigned int i = 0; i < vertexs.size(); i++)
{
cout << "index: " << i << ", distance : " << vertexs[i]->distance << endl;
}
}
void clearVertexs(vector<vertex*>& vertexs)
{
auto it = vertexs.begin();
while (it != vertexs.end())
{
delete *it;
it++;
}
vertexs.clear();
}
int main()
{
vector<vertex* > vertexs;
loadVertexs(vertexs);
processVertexs(vertexs);
printVertexs(vertexs);
clearVertexs(vertexs);
}







 Dijkstra算法是一种用于寻找加权图中单源最短路径的贪心算法。从源点开始,逐步确定每个顶点到源点的最短路径,通过不断更新邻接节点的距离实现。在邻接矩阵或邻接表表示的图中,该算法特别适合于连接稀疏的图。通过选择当前未知顶点集中距离源点最近的顶点,保证了最短路径的正确性。
Dijkstra算法是一种用于寻找加权图中单源最短路径的贪心算法。从源点开始,逐步确定每个顶点到源点的最短路径,通过不断更新邻接节点的距离实现。在邻接矩阵或邻接表表示的图中,该算法特别适合于连接稀疏的图。通过选择当前未知顶点集中距离源点最近的顶点,保证了最短路径的正确性。
















 944
944

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








