深度强化学习系列(1): 深度强化学习概述

机器学习是人工智能的一个分支，在近30多年已发展为一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等的学科。强化学习(RL)作为机器学习的一个子领域，其灵感来源于心理学中的行为主义理论，即智能体如何在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。它强调如何基于环境而行动，以取得最大化的预期利益。通俗的讲:就是根据环境学习一套策略,能够最大化期望奖励。由于它具有普适性而被很多领域进行研究，例如自动驾驶,博弈论、控制论、运筹学、信息论、仿真优化、多主体系统学习、群体智能、统计学以及遗传算法。

** RL和监督式学习, 非监督学习之间的区别:**
，其主要分为监督学习、非监督学习、深度学习和强化学习(见图1),其中三个之间的区别在于以下三点：

• (1)、RL并不需要出现正确的输入/输出对，也不需要精确校正次优化的行为。它更加专注于在线规划，需要在探索（在未知的领域）和遵从（现有知识）之间找到平衡,其学习过程是智能体不断的和环境进行交互,不断进行试错的反复练习。
• (2)、RL的不同地方在于：其中没有监督者，只有一个reward信号；反馈是延迟的，不是立即生成的；时间在RL中具有重要的意义。
• (3)、 RL并不需要带有标签的数据,有可以交互的环境即可。

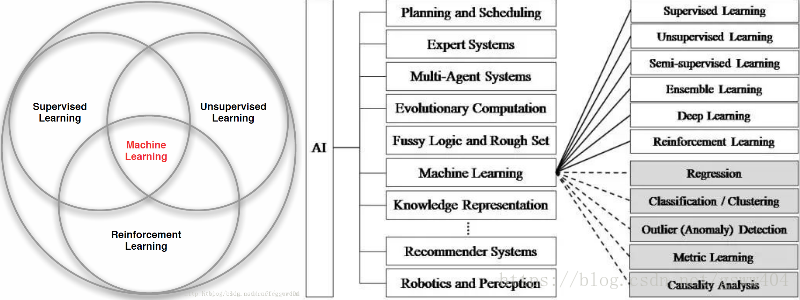
基于此,普通机器学习方法和强化学习之间的的关系已描述清楚。我们知道机器学习算法和深度学习可以做分类，回归、时间序列等经典问题，这已经在很多应用场景，例如语音、文字语义等基础性的人类认知方面取得非常大的突破，但是为什么还要学习强化学习呢？不得不从其应用场景说起。

RL目前的应用场景:

• 自动驾驶: 自动驾驶载具（self-driving vehicle）
• 控制论(离散和连续大动作空间): 玩具直升机、Gymm_cotrol物理部件控制、机器人行走、机械臂控制。
• 游戏: Go, Atari 2600(DeepMind论文详解)等
• 理解机器学习: 自然语言识别和处理, 文本序列预测
• 超参数学习: 神经网络参数自动设计
• 问答系统: 对话系统
• 推荐系统: 阿里巴巴黄皮书（商品推荐），广告投放。
• 智能电网: 电网负荷调试, 调度等
• 通信网络: 动态路由, 流量分配等
• 物理化学实验: 定量实验,核素碰撞,粒子束流调试等
• 程序学习和网络安全: 网络攻防等

说了这么多,都是关于其背景和应用场景的话题（相关论文见RL-an overview中）,那么到底什么是RL, 又是怎么工作的? 以及工作过程中会受那些因素的影响呢？ 下文继续回到Rl主题上.

一、强化学习基本组成及原理

1.1、RL结构图:

RL是一种智能体和环境之间不断试错的方法, 通过不断的交互以取得最大的累计期望奖励，它由环境, 智能体和奖励尺度三部分组成，见图：

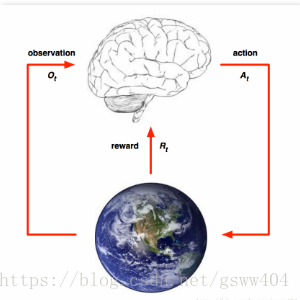
在图中, 大脑部分代表智能体(Agent), 地球代表环境(Environment)
执行过程： 智能体(Agent)通常从环境中获取一个$O_t$, 然后Agent根据$O_t$调整自身的策略做出一个行为(Action:$A_t$)反馈给环境, 环境根据Agent的动作给予Agent一个奖励$R_t$,经过这样，智能体和环境之间进行连续的交互学习，得到了一个{ $O,A,R$}的交互历史序列。通常历史序列由观测、行为、奖励三部分组成，被定义为：
$$H_t=O_1,A_1,R_1,\dots ,O_t,A_t,R_t$$
同时状态被定义为函数$f(\cdot )$的映射： $S_t=f(H_t)$，接下来将会对序列通过MDP进行描述：

1.2、马尔科夫决策过程（MDP）

马尔科夫决策过程是一个序列决策问题，它由很多的马尔科夫过程元组组成。 首先了解几个名词:
马尔科夫性： 指系统的下一个状态$S_{t+1}$ 仅与当前状态 $s_t$有关，表示为：
$$P[S_{t+1}|S_t]=P[S_{t+1}|s_1,s_2,...,s_t]\text{\hspace{1em}(1)}$$
** 马尔科夫过程：** 它是一个二元组$(S,P)$, 其中$S$为有限状态机，$P$为状态转移概率。且状态转移概率矩阵为：

$$P=\left[\begin{array}{ccc}{P}_{11}& \dots & P_{1n}\\ .& & .\\ .& & .\\ P_{n1}& \dots & P_{nn}\end{array}\right]\text{\hspace{1em}(2)}$$
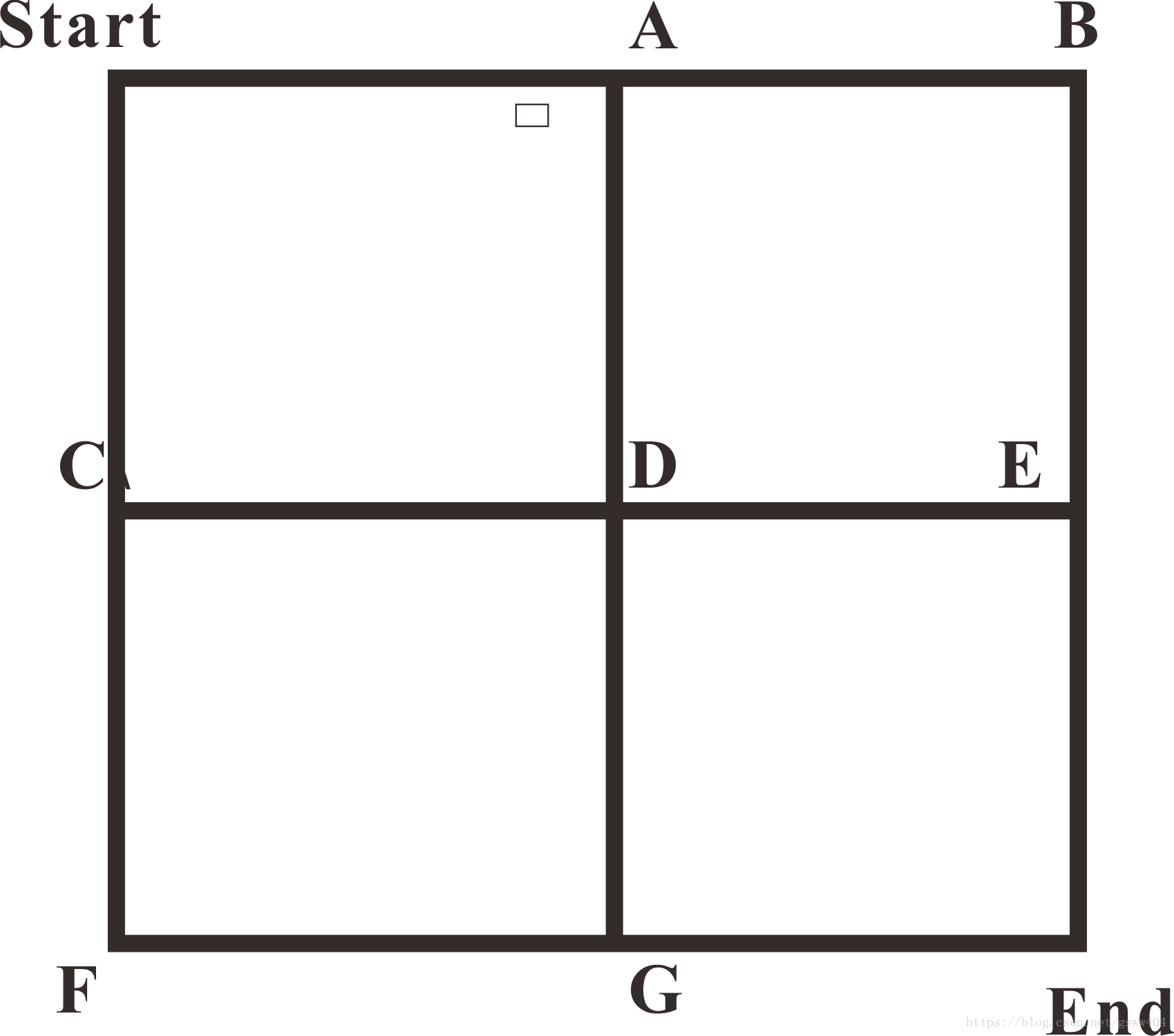
举个例子说明一下（如图）：如果给定状态转移概率矩阵P,即每个点到下一个点的状态转移概率，那么从Start出发到End结束存在多条马尔科夫链（多条路径），其中每个链上就是马尔科夫过程的描述。但马尔科夫过程中并不存在action和奖励。因此，从Start开始到end是一个序列决策问题，需要不断的选择路线，以取得最大收益。接下来是MDP

**马尔科夫决策过程（MDP）：** 通常情况马尔科夫决策过程用元组<$S,A,P,R,\gamma$>描述: $S$: 有限状态集 $A$：有限动作集 $P$：状态转移概率 $R$：回报函数 $\gamma$：折扣因子，用来计算累计回报。

上述是MDP的组成，而我们关心的是它如何工作，继续前面的走方格例子，从Start开始，有两个行为（向右走，向南走），走不通的方向都有$P=\frac{1}{4}$的概率且有不同的奖励，一直反复的走，直到走到End结束，在这个过程中会形成不同的序列,例如序列1：
{ ( S t a r t , R i g h t , P , R 1 ) , ( A , R i g h t , P , R 2 ) , ( B , S o u t h , P , R 3 ) , ( E , S o u t h , P , R 4 ) , ( E n d , S o u t h , P , R 5 ) } \left\{(Start,Right,P,R1),(A,Right,P,R2),(B,South,P,R3),(E,South,P,R4), (End,South,P,R5)\right\} { (Start,Right,P,R1),(A,Right,P,R2),(B,South,P,R3),(E,South,P,R4),(End,South,P,R5)}
这只是其中一条路径，那从Start到End那条路劲带来的收益最大呢？就需要每一步进行决策，而决策就需要用到策略。下文继续：

1.3、强化学习的目标及Agent的要素：

目标： 根据环境状态序列，找到一套最优控制策略，以实现最大累计期望奖励。

1.3.1 第一要素 ---- 策略

那么什么是策略呢？ 通常情况下被定义为是从状态到行为的一个映射，直白说就是每个状态下指定一个动作概率，这个可以是确定性的（一个确定动作），也可以是不确定性的。
(1)非确定策略： 对于相同的状态，其输出的状态并不唯一，而是满足一定的概率分布，从而导致即使是处在相同的状态，也可能输出不同的动作，表示为：
$$\pi (a|s)=P[A_t=a|S_t=s]\text{\hspace{1em}(3)}$$
(2)确定行策略： 在相同的状态下，其输出的动作是确定的，表示为：
$$a=\pi (s)\text{\hspace{1em}(4)}$$

如果给定一个策略，就可以计算最大化累计期望奖励了，通常奖励分为及时奖励和长久累计期望奖励，
**及时奖励：**实时反馈给Agent的奖励$r_t$，举例：当玩具直升机根据当前的作态做出一个飞行控制姿势时，好坏会立即得到一个奖励。
**累计期望奖励：**通常指一个过程的总奖励的期望，比如直升机从飞起到降落整个过程。
通常累计期望奖励被定义为：
$$G_t=R_1+\gamma R_2+{\gamma }^2{R}_3+\cdots +{\gamma }^{k-1}{R}_k=\sum _{k=0}{\gamma }^k{R}_{t+k+1}\text{\hspace{1em}(5)}$$

假如在策略$\pi$下，从前文的Start出发，则有不同的路径
$$\begin{gathered} Start\to A\to B\to E\to End \\ Start\to C\to D\to G\to End \\ .... \end{gathered}$$

每个路径的累计回报$G_t$不同，且在随机策略下$G_t$是随机变量，但它们的期望是一个确定值，因此而被用作值函数的估计。

1.3.2 第二要素 ---- 值函数

当Agent采用某个策略