线性模型假设的问题
如上图，对非线性类边界的数据进行分类
一个解决方案是将数据映射到更高维的空间，就变成线性可分的了。
ϕ\phiϕ 是一个映射函数，将x从一个低维空间映射到高维空间。
ϕ\phiϕ 可不可以是一个线性函数？
ϕ(x)=WTx\phi(x) = W^Txϕ(x)=WTx 并不能起到将x映射到高维空间的效果。
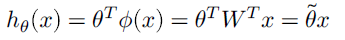
这个函数本质上还是线性的，没有什么变化。
非线性特征
σ\sigmaσ是一个非线性函数，但是并不改变矩阵的维度。可以是cosine函数之类的。
两层神经网络
矩阵形式
非线性层
线性的函数，只能在给定空间中进行线性划分，能拟合直线或者空间中的超平面。
加入非线性层，比有更强的拟合效果，能拟合曲线，空间中的曲面等。
全连接神经网络一般形式
全连接的神经网络一般有L层，又称多层感知机。
θ=W1,...,WL\theta={W_1,...,W_L}θ=W1,...,WL
有些时候，每一层还会加一个偏移项 bi
Zi+1=σi(ZiWi+bi)Z_{i+1} = \sigma_i(Z_iW_i+b_i)Zi+1=σi(ZiWi+bi)
如何训练？
计算两层网络的梯度
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
