树状数组
前缀和,当原数组进行修改的售后,需要付出O(n)的代价。

ti 也可以理解为其二进制的最低位的 1,与其后的 0 组成的 2 进制数

lowbit(i) = i&(~i+1) = i&-i
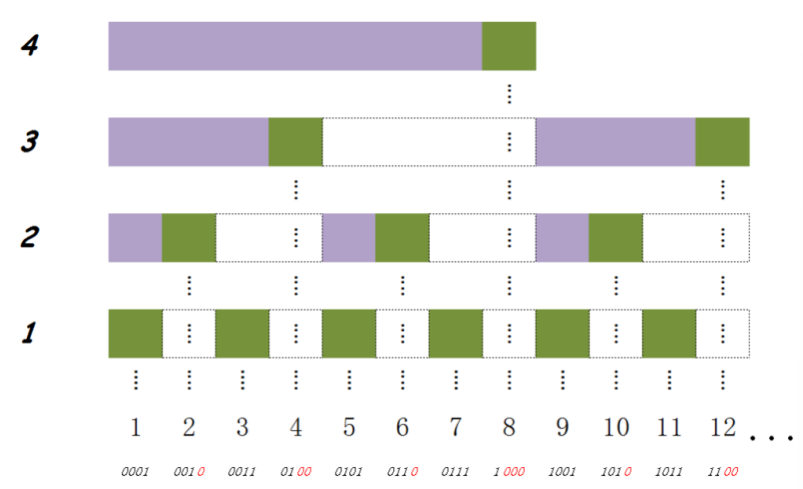
如果要查询区间 [1-i] 的和,需要树状数组进行多段拼接, 树状数组d中, d[i] 表示 (i -ti, i] 的和,令 y = i -ti, 那么左侧紧邻的一段为 (y-ty, y] ,直到 加上(0, x] 这个区间为止。

树状数组修改,当原数组a 中某元素 a[i] 修改时,只有部分树状数组 d 中元素涉及a[ i ],只用修改部分值,O(logn).
当a[i] 修改时,如何找到要修改的 d 中元素

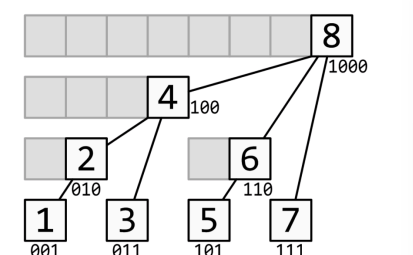
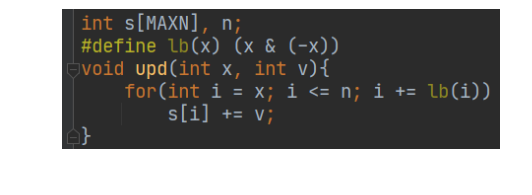
树状数组的应用
求逆序对(二位偏序问题)

二维偏序,首先按其中一个维度排序。另一个维度是无序的。
按照第二个维度的值,向树状数组中进行插入操作,每次插入完一个数,假设其第二维的值为 x ,求 ask(n)- ask(x) , n是第二维的最大值,那么就求出了 当前 在该数之前,第二维大于x,即 第二维值属于(x,n] 的数的数量。
最长上升子序列
#define lb(x) (x &(-x))
using namespace std;
const int N = 1e6 +10;
// 建立树状数组
int s[N] = {0};
void upd(int x,int v){
for(int i=x;i <N;i+=lb(i) )
s[i] = max(s[i],v);
}
int ask(int x){
int ans = 0;
for(int i =x;i >=1;i-=lb(i))
ans = max(ans,s[i]);
return ans;
}
int main(){
//freopen("a.in","r",stdin);
int n;
cin >>n;
int ans = 0;
for(int i = 0;i < n;i++) {
int tmp;
cin >> tmp;
int a = ask(tmp-1);
a++;
upd(tmp,a);
}
ans = ask(N-1);
cout << ans<<endl;
}
线段树
在 O(log n)的时间内维护区间信息。
- 具体来说支持单点修改、区间修改、区间查询(区间求和,求区间最大值,求区间最小值)等操作
- 只用线段树维护信息,信息起码得是区间可合并的,加减乘除,最大最小都可以,中位数就不行
线段树的基本结构
使用数组构造二叉树,父节点为 i, 子节点为 2i和 2i+1
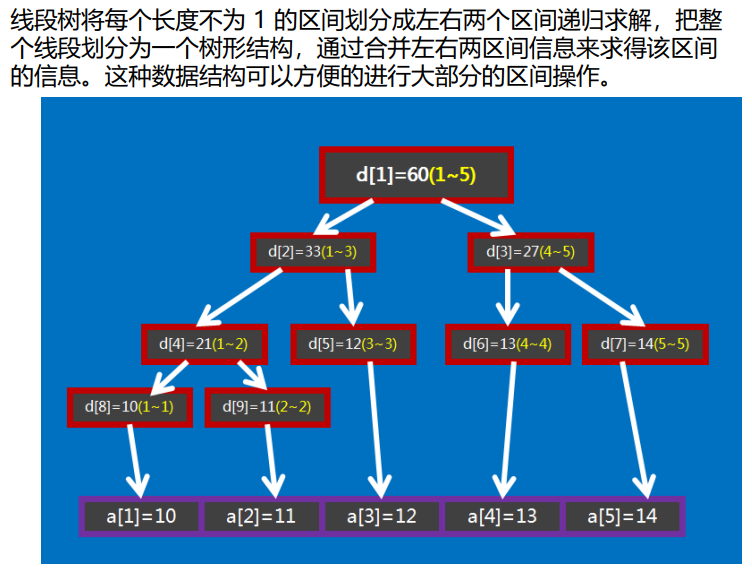

维护区间和的线段树建立
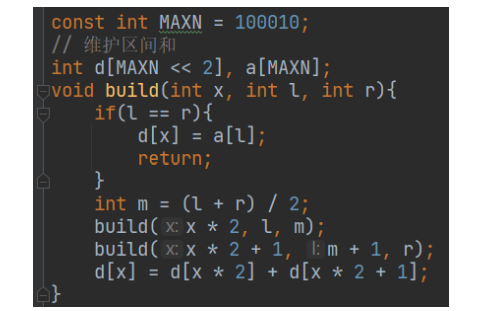
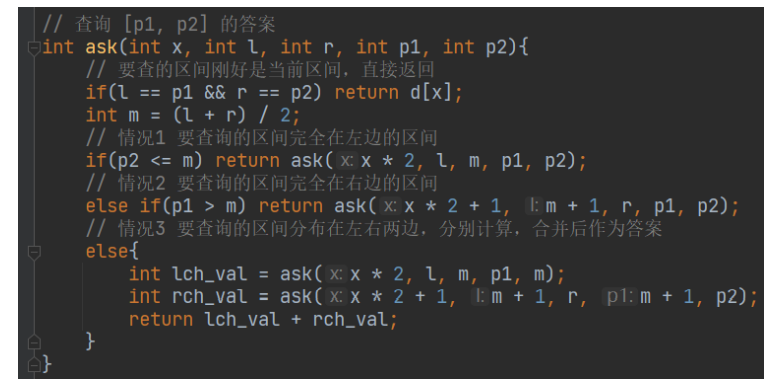
单点修改






 本文介绍了树状数组和线段树在计算机科学中的应用,特别是如何利用它们在O(logn)时间内进行区间修改、查询和求逆序对。重点讲解了如何通过lowbit操作优化区间求和,以及在修改原数组元素时的高效策略。
本文介绍了树状数组和线段树在计算机科学中的应用,特别是如何利用它们在O(logn)时间内进行区间修改、查询和求逆序对。重点讲解了如何通过lowbit操作优化区间求和,以及在修改原数组元素时的高效策略。
















 349
349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








