基于频谱熵的铁质隧道识别

汽车雷达增强型铁质隧道识别

摘要

本文提出了一种新型的铁质隧道识别方法，以克服由于铁质隧道杂波导致的目标或车辆检测性能下降的问题。尽管已有一些针对汽车雷达传感器在路面反射和衍射方面的研究，但这些研究大多未考虑诸如铁质隧道等具有较强反射特性的结构密集分布的情况。所提出的方法通过分析在不同道路条件下接收到的雷达信号的频谱特性，来测量谱展宽程度。该方法能够成功检测铁质隧道。此外，实验结果表明，在自适应巡航控制（ACC）下，铁质隧道内前方目标车辆的早期检测以及漏检问题得到了改善。

索引词

汽车雷达，铁质隧道，自适应巡航控制（ACC），车辆

一、引言

随着对安全和驾驶辅助的关注增加，各种安全传感器正被引入汽车中。由于雷达在恶劣天气条件或较差的道路环境下相较于许多其他传感器表现出更强的鲁棒性，全球汽车雷达的安装率正在迅速上升。随着自动紧急制动或自动驾驶等安全问题在未来变得至关重要，对自主雷达传感器的需求将呈爆炸式增长[1]–[3]。随着汽车雷达的普及，基于雷达的自适应巡航控制（ACC）[4]成为驾驶员最实用的便利功能之一。使用ACC功能，驾驶员不仅可以减少驾驶疲劳，即使在因恶劣天气导致能见度较低的情况下，也能确保安全性。然而，如果铁隧道或隔音墙等结构反射了较强的电磁波，则可能产生较强的杂波信号，其强度甚至超过来自目标的反射信号，从而导致雷达检测性能下降。在这种情况下，汽车雷达所具备的感知鲁棒性优势可能无法得到保障。由于用于提升雷达检测性能的硬件资源有限，必须采用信号处理技术来克服因道路环境引起的性能下降问题。

关于路面反射和衍射现象，已有一些针对汽车雷达传感器的研究[5]–[7]。这些研究发现，雷达检测性能受路面表面状况和道路坡度的影响。同时，有关道路杂波结构的研究报道较少[8],[9]。这些研究基于超宽带脉冲雷达，因此将其应用于调频连续波（FMCW）雷达等其他调制方式[10]–[12]是不充分的。此外，已有研究探讨了区分桥梁或护栏等结构与道路上静止物体的方法[13]–[15]。然而，大多数研究未考虑铁质隧道等具有强反射的结构密集分布的情况。

本文提出了一种新颖的铁质隧道识别方法，以克服因铁质隧道杂波导致的目标或车辆检测性能下降问题。该方法通过分析在不同道路条件下接收到的雷达信号的频谱特性来识别铁质隧道。我们观察到，铁质隧道会在宽频带范围内产生高强度散射。因此，所提出的方法引入熵概念来度量谱展宽程度。本文所使用的实验数据来自用于自适应巡航控制的77 GHz前向调频连续波雷达。我们证明了所提出的方法能够成功检测铁质隧道。此外，结果表明，在自适应巡航控制中使用雷达时，通过克服铁质隧道周围或内部检测性能的下降，目标车辆在铁质隧道内的漏检问题得到了改善。

本文的结构如下：在第二节中，介绍了研究中使用的雷达模型，并分析了不同道路环境下接收信号的频谱特性。随后，详细阐述了提出的方法。在第三节中，给出了识别铁隧道的实验结果以及自适应巡航控制性能提升的结果。最后，在第四节中对我们的工作进行了总结和结论。

II. 铁质隧道识别

在本节中，我们简要解释并数学描述了雷达模型。然后，展示了雷达信号在不同道路条件下的频谱特性。提出了一种基于频谱展宽特性识别铁隧道的新方法。

A. 雷达模型

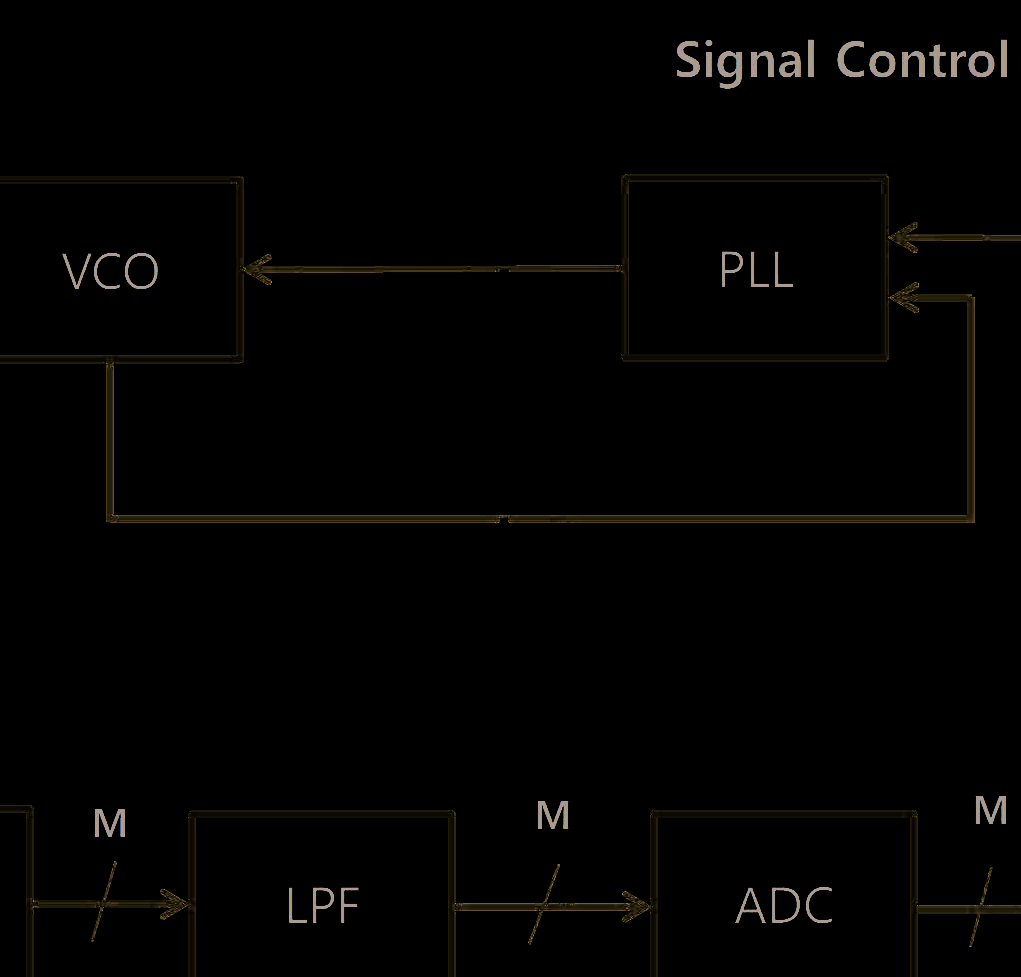
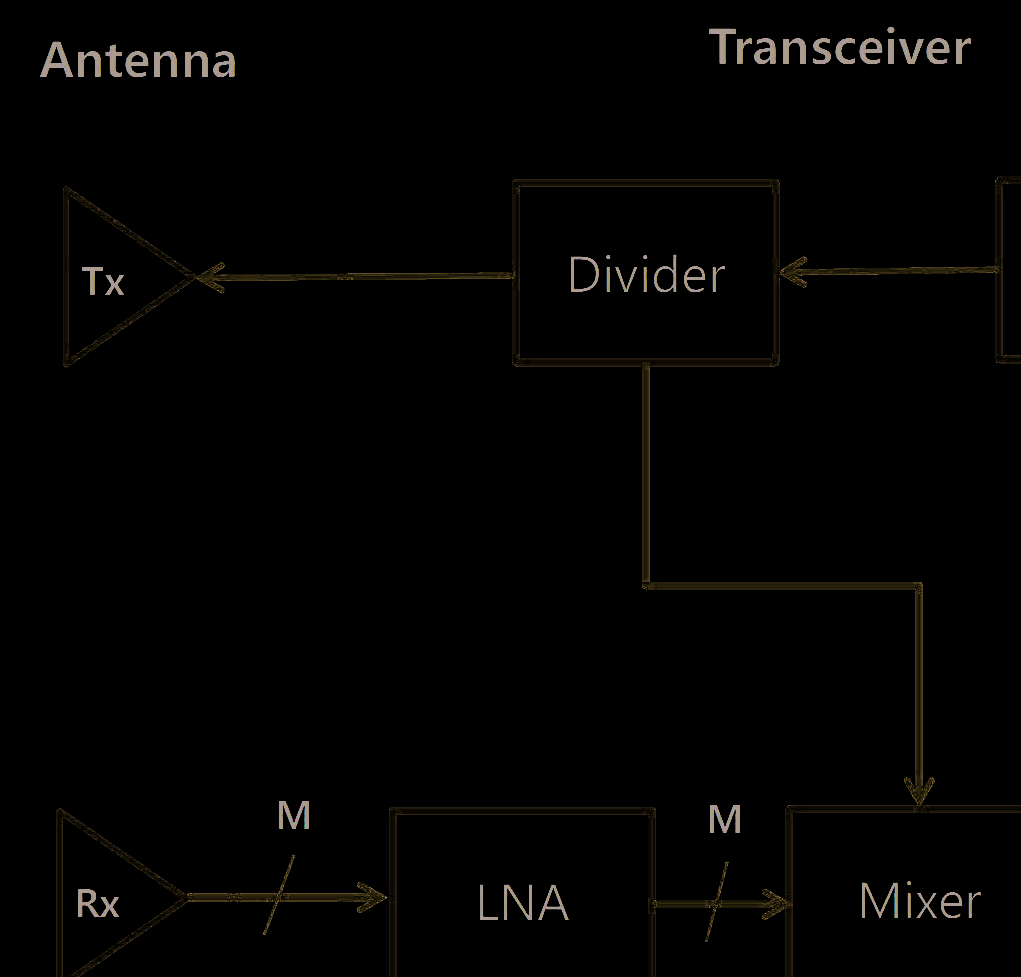
本文中，我们采用了一款77 GHz前向调频连续波长距离雷达。图1显示了调频连续波雷达的结构。该雷达由天线模块、收发单元以及信号控制与处理单元组成。其中，天线模块将射频电信号转换为电磁波；收发单元负责生成射频信号并处理接收到的射频信号；信号控制与处理单元则控制射频信号并处理接收信号。天线模块包含在印刷电路板上实现的线性贴片阵列天线。信号控制与处理单元负责调频连续波调制和雷达扫描的调度。发射信道为单信道，接收信道由 K个均匀线性阵列组成。时间，即一个 scan，包括发射、接收和信号处理过程。单个 scan持续时间为 50毫秒。在每个 scan处发射相同的信号。如果调频连续波雷达发射的信号被 L个目标反射，则第 k个阵列中的接收信号定义为

$$
sk(t)= \sum_{i=0}^{L-1} Ak(i)cos(2πf(i)t+ φk(i)).
$$

Ak(i) 是第 k个天线接收到的来自每个目标的反射信号的幅度。 φk(i) 是每个接收信号的相位分量。 f(i) 由 fr(i) （即根据目标距离引起的频率差异）和 fd(i)（由于雷达与各个目标之间的相对速度引起）组成。 fr(i) 和 fd(i) 可分别使用公式 (2) 和 (3) 计算， i.e.，

$$
fr(i)= \frac{2B}{cT} R(i)
$$

and

$$
fd(i)= \frac{2fc}{c} V r(i)= \frac{2}{λ} V r(i)
$$

其中 B是带宽， T是啁啾持续时间， c是光速， fc 表示中心频率， R(i)和 Vr(i) 分别是距离和相对速度。 sk(n) 是 sk(t) 的离散时间信号，可以表示为

$$
sk(n)= \sum_{i=0}^{L-1} Ak(i)cos(2πf(i)n+ φk(i))
$$

其中 n(0 ≤ n< N)是单个 scan期间接收信号的离散时间索引， N是单个 scan中的总采样数。

如果对接收信号进行短时傅里叶变换（STFT），则可以表示为

$$
Sk(f, m)= \sum_{n=0}^{N-1} sk(n+(m− 1) · N)e^{-j 2πf/N ·n}
$$

其中 f是频率索引， m是 scan索引。频域中的幅值响应可以表示为

$$
P(f, m)= \left| \sum_{k=0}^{K-1} Sk(f, m) \right|.
$$

B. 铁质隧道的频谱特性

为了理解铁隧道对雷达信号特性的影响，我们分析了其频谱特性。为了仅提取铁隧道的频率特性，我们利用在普通道路、高速公路以及铁质隧道入口和内部所获取的信号，研究了其频率特性。图2展示了在不同道路条件下接收信号的短时傅里叶变换幅值响应。图2a显示，在正常道路条件下，20–30 kHz频段具有高强度（红色），这意味着前方存在一个与自车速度几乎相同的单一目标。浅绿色或黄色的斜线对应于与自车速度不同的车辆或诸如路标等静止物体。图2b显示的是高速公路情况，与图2a类似，目标车辆在整个频谱范围内均表现出高强度。在恒定频段出现高强度的现象意味着自车与目标之间的相对速度保持不变。图2c显示的是铁隧道的入口点，在初始阶段（ t< t0），窄频带内出现高强度。随着车辆接近隧道，高强度出现在更宽带宽范围内。图2d显示的是铁隧道内部的情况，由于隧道内部的铁质结构，整个频段均观测到高强度响应。铁隧道导致接收信号在更宽带宽内产生频谱响应。

因此，如果能够对接收信号的频谱扩展进行定量测量，则可以实现对铁隧道的识别。

C. 测量频谱扩展

为了识别上述铁隧道，需要对频谱扩展的程度进行定量测量。为实现这一目标，可优先考虑频谱扩展的标准差。

标准差可以通过计算频率幅度响应来作为频谱扩展的度量

$$
σ(m)= \sqrt{ \frac{1}{N} \sum_{f=0}^{N-1}(P(f, m)− P(f, m))^2 }
$$

其中 P(f, m) 是幅值响应相对于频率的平均值。通常情况下，数据分布越不均匀，即与平均值的差异越大，标准差也越大。然而，标准差对数据中的脉冲分量和剧烈波动非常敏感。

本文提出了一种利用熵的概念来测量频谱扩展的新方法。香农熵(SE)通常用于衡量信息的不确定性，其表达式如下

$$
SE= - \sum_{i=0}^{N-1} p(i) \log_2 p(i).
$$

这里， p(i) 是概率密度函数。如果频率幅度响应扩散到较宽的频带，则 p(i) 呈均匀分布，此时谱熵（SE）预期具有较大值。相反，当 p(i) 集中在较窄的频带时，幅值的概率分布较窄，SE 的值较小。提出的方法通过利用频率幅度响应的概率分布计算 SE 来衡量频谱扩展的程度。为了获得接收信号频率响应幅值的概率分布，我们定义 pm(i) 为

$$
pm(i)= \frac{\text{(number of samples per scan ∈ Bi)}}{N},(0 ≤ i< I)
$$

其中 Bi={P(f, m)|Pmax · i/I ≤ P(f, m) < Pmax ·(i+1)/I} 且 Pmax是 P(f, m) 的最大值。因此 pm(i) 表示在区间 Bi内找到的采样数与第 m个 scan中的总采样数 N之比。

提出的谱展宽度量可表示为

$$
S(m)= - \sum_{i=0}^{I-1} pm(i) \log pm(i).
$$

在正常道路情况下，雷达信号的频率响应可能由于来自多个目标的反射信号而出现多个频率峰值。当道路上存在大量车辆或静态物体时，由目标引起的频率分量是明显的，且频率峰值的数量与目标数量成正比。因此，时频谱可能在某些特定频带中显示出集中峰值，谱展宽度量SE变得较小。另一方面，由于铁隧道中的铁质结构密集分布，时频谱广泛分布。此外，即使结构由相同材料构成，由于反射信号的衰减差异，反射信号的强度也会随距离变化。另外，由于铁质结构不位于自车的同一方位面上，并且在铁质结构的仰角方向上分布在不同角度，导致反射信号的强度存在差异。因此，反射雷达信号的时频谱强度分布在更宽带宽内，谱展宽更大。这种谱展宽的来源并非超宽带特性，而是铁隧道中的密集多径场景，因为我们已使用 77GHz调频连续波雷达进行了实验。

为了更好地了解铁隧道中的频谱扩展情况，我们提供了两个示例。表I列出了经纬度坐标、入口时间以及两个铁质隧道的长度。根据表I中列出的道路条件，计算了式 (7)中的标准差和式(10)中的谱展宽度量，结果如图3所示。

图3a显示，在约13 s时入口点处的标准差和频谱扩展值均逐渐增加。然而，在进入铁隧道之前的时间点 5s处，标准差表现出显著差异

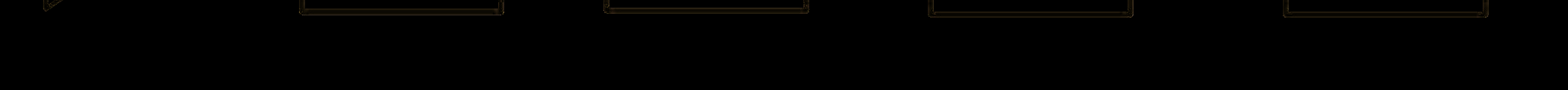
高值，而谱展宽度量则保持相对稳定。标准差的大幅波动可能会恶化铁隧道的识别。图3b显示出与图3a相似的趋势。然而，在隧道内部，标准差再次下降并出现波动，这一结果可能使得铁隧道的识别变得困难。另一方面，谱展宽值在驶出隧道之前一直保持在较高水平。

III. 实验结果

在本节中，我们展示了在具有多种铁质隧道的真实环境中使用实测数据进行的实验结果，以验证第二节中提出的铁质隧道识别方法的可行性。此外，还展示了在各种铁质隧道中自适应巡航控制性能的提升。

A. 铁隧道识别

为了验证铁隧道可以通过提出的谱展宽方法进行识别，我们使用在不同铁质隧道获取的实测数据对提出的方法进行了测试。谱展宽度量的铁隧道识别阈值设定为0.35；如果超过该阈值，则视为隧道。实际隧道进入时间用虚线表示，隧道识别时间用实线表示。图4a显示，普通隧道的谱展宽度量低于阈值，即0.35，因此未被识别为铁隧道。图4b–4d展示了在表I列出的两个铁隧道中，改变车辆、雷达样本和实验日期所得到的结果。图4表明，当隧道进入雷达视场范围内时，由于信号提前接收到，总能在进入之前被识别为铁隧道。

表I 铁隧道剖面
| Case | 地理坐标 (纬度, 经度) | Time (s) | 隧道长度 (km) | 实验 Date |
| — | — | — | — | — |
| A | (37.27, 127.08) | 15.25 | 1.0 | 2014年1月27日 |
| B | (37.17, 127.03) | 4.25 | 0.7 | 2014年02月05日 |

表II 各类隧道的频谱扩展和剖面
| Case
A | Type
正常 | 地理坐标 (纬度, 经度) | 时间， t0
(s) | 识别时间， tr
(s) | 长度 (km) | 之前识别 | 之后识别 | 实验 Date |
| — | — | — | — | — | — | — | — | — |
| | (37.25, 127.09) | 4.00 | - | 0.3 | 0.14 | - | 2013年10月08日 |
| B | iron | (32.27, 127.08) | 15.50 | 14.00 | 1 | 0.23 | 0.41 | 2014年01月06日 |
| C | iron | (32.27, 127.08) | 12.25 | 9.50 | 1 | 0.21 | 0.58 | 2014年02月05日 |
| D | iron | (32.17, 127.03) | 7.50 | 3.50 | 0.7 | 0.17 | 0.46 | 2014年1月14日 |

表II总结了隧道入口的经纬度坐标、隧道进入时间、铁质隧道识别时间、隧道长度以及在2s识别前后谱展宽度量的平均值。我们可以确认，在隧道识别前后，谱展宽度量的平均值之间存在显著差异。

为了确保铁隧道识别的阈值合理，我们研究了铁隧道识别时间随阈值变化的情况。图5展示了将检测阈值从0.05以0.05为步长逐步增加至0.7时，铁隧道识别时间的变化曲线。从图5可以看出，随着阈值的增加，检测时间也随之增加。然而，当阈值在0.3到0.5之间时，检测时间相对稳定。在案例B、C和D中也观察到了类似的趋势，我们认为合理的阈值范围应在0.3到0.45之间。但为了提高阈值的鲁棒性，可能需要利用更大量的实验数据进行统计分析。

B. 早期目标检测与防止目标丢失

为了检验所提出的铁质隧道识别方法在自适应巡航控制中的实用性，进行了实验以确定在靠近铁隧道时自车车道内的目标或车辆被检测到的速度。图6显示了进入铁隧道后，在检测前方目标车辆时应用与不应用铁质隧道识别方法的检测结果。图6a显示了用于隧道识别的频谱扩展，以及该隧道在14.25s处被识别。图6b显示了频域目标检测阈值的平均值。虚线表示由有序统计恒定虚警率（OS‐CFAR）算法计算出的目标检测阈值的平均值[16]，实线表示通过所提出的铁隧道检测方法调整后的目标检测阈值的平均值。

如图6b所示，由于铁隧道内存在大量杂波，OS‐CFAR的阈值水平变得非常高，这一高阈值可能导致铁隧道内的目标车辆漏检。另一方面，通过铁质隧道识别降低阈值（实线），可以降低目标漏检的风险。图6c显示了目标车辆沿运动距离的检测轨迹。我们可以确认，在通过铁质隧道识别调整目标检测阈值后，目标车辆能够更早地被检测到。

初始目标检测时间对自适应巡航控制性能至关重要。如果目标车辆被检测到的时间过晚，正在加速的自车将进行急减速，从而导致行驶状况不舒适，并且当自车速度较高时，碰撞风险可能增加。此外，若自车与后方车辆的距离较近，急减速还可能引发追尾碰撞。图6d显示了在隧道识别后首次检测到目标时（17.15s）接收到的雷达信号的频率响应，我们可以观察到在40‐100 kHz范围内的杂波水平显著升高。由于隧道附近或内部的杂波水平较高，当铁隧道高于目标车辆的峰值时，无法检测到目标车辆。因此，我们需要通过铁质隧道检测来控制目标检测阈值。

为了进一步说明所提出的铁质隧道检测方法在自适应巡航控制中的实用性，我们进行了实验，以确定铁质隧道结构检测的可靠性。图7a显示了用于隧道识别的谱展宽度量，铁隧道在8.75 s时被识别。图7b显示了频域中目标检测阈值的平均值，该阈值的调整方式与图6所示类似。图7c显示了目标车辆沿距离方向的检测轨迹，在铁隧道内未出现目标丢失情况。我们可以确认，在应用铁隧道识别后，检测轨迹中间未发生目标遗漏。

自适应巡航控制期间前方目标的丢失会导致突然加速，可能增加前向碰撞风险。图7d显示了铁隧道内目标因铁隧道结构引起的高杂波水平而可能被遗漏时的雷达信号频率响应。

IV. 结论

本文提出了一种利用雷达识别铁隧道的新方法。通过频谱分析比较了各种道路条件，并提取了铁隧道条件下的特征。提出了基于熵概念的频谱扩展方法，以定量测量铁质隧道的频谱特性。实验表明，频谱扩展是检测铁质隧道的一个非常有用的特征。此外，在内部或附近铁隧道中存在大量杂波，会恶化目标检测性能，而铁隧道识别可能有助于自适应巡航控制系统提升性能和鲁棒性。

尽管我们已使用实地数据对提出的方法进行了测试，但仍需要进行更多的实地实验，以对结果进行统计分析，并找到铁质隧道识别的可靠阈值。