电动汽车制动协调控制

第8章 电动汽车的制动协调控制

吕晨1, 1 12王洪和曹东璞克兰菲尔德大学，贝德福 德，英国2滑铁卢大学，加拿大安大略省滑铁卢

8.1 引言

日益加重的环境负担和日益枯竭的能源资源要求汽车更加清洁和高 效（Martinez等人，2016）。研究表明，在城市驾驶工况下，约 有三分之一到一半的动力装置能量消耗在减速过程中（Gao等人， 2001；张等人，2012；吕等人，2014ac；Crolla和Cao，2012）。

在电动化车辆的关键技术中，再生制动系统能够在制动过程中将车 辆的动能转化为电能，有效提高燃油经济性，已成为汽车制造商、 零部件制造商和全球研究人员研发的热点课题（Sovran和 Blaser，2006；吕等人，2015ac；Chiara和Canova，2013； Kum等人，2011，VonAlbrichsfeld和Karner，2009）。

大多数生产的电动化车辆，包括丰田普锐斯、日产聆风和特斯 拉ModelS，都配备了再生制动（中村等人，2002；Ohtani等人， 2011；弗莱明，2013）。然而，为了确保车辆的制动性能，仍需要 机械制动。与传统摩擦制动相比，再生制动具有截然不同的动态特 性。例如，电机制动力矩响应迅速且准确，而再生制动则显著受到 电机和电池运行条件的影响。此外，其通过变速箱、传动轴和半轴 传递至车轮的传动路径，比安装在车轮侧的摩擦制动器要长得多。

这些特点不仅在正常和极限驾驶工况下为提升车辆动力学性能提供 了巨大潜力，也对现有的制动理论和控制方法带来了巨大挑战。因 此，研究再生制动与摩擦制动协调的机理及控制方法具有重要意义。

8.1.1 制动能量管理

制动能量管理的任务是通过合理分配再生制动力与摩擦制动力，最 大限度地挖掘利用再生制动的潜力，尽可能提高电动汽车（EV）的 能源效率。在再生制动控制方面，目前的研究主要集中在正常减速 过程，旨在提高再生效率以及再生制动与摩擦制动之间的协调控制。

高等人（2001）提出了两种再生制动策略。在现有研究中，汽车制 造商、零部件制造商和全球研究人员已在系统设计和控制方面开展 了研究与开发。丰田开发了电液制动系统，并成功应用于商业化混 合动力汽车（HEV）（中村等人，2002）。日立开发了具有电动驱 动电机和滚珠丝杠特征的电动智能制动系统，并将其应用于日产聆 风电动汽车（青木等人，2007）。一种配备能量回收系统的动力总 成被设计出来（帕拉迪尼等人，2007）。超级电容器可用于回收再 生能量。在再生制动控制方面，当前的研究主要集中于再生制动与 摩擦制动之间的协同工作（乌尊奥卢和阿拉姆，2007）。针对后驱 电动小型货车设计了一种新的再生制动控制策略（张等人， 2014a,b）。提出了一种协调再生制动与气压制动的控制策略，以 回收制动能量并提高燃料电池城市客车的燃油经济性（张等人， 2013）。为进一步提高复合制动控制性能，提出了一种基于开关电 磁阀的新型控制方法（吕等人，2014ac）。

8.1.2 动态协调控制

动态协调控制针对的是动态过程。与传统内燃机（ICE）汽车相比， 配备再生制动的电动汽车具有三种不同的制动状态：摩擦制动、再 生制动和复合制动。这三种制动状态
276电动汽车建模、动力学与控制
可能在一个制动过程中独立发生或频繁相互切换。特别是，由于电 驱动系统的动力学特性与传统摩擦制动系统有很大不同，在减速过 程中引入电动机扭矩可能会成为系统和车辆层面振动和冲击的新来 源。此外，摩擦制动力的动态调节也可能导致制动回路中的压力波 动，从而对制动性能、制动舒适性甚至车辆的能源效率产生负面影 响（吕等人，2014ac）。因此，确定电驱动系统的动力学特性及 其对复合制动控制的影响已成为再生制动控制中的重要方面。同时， 如何动态耦合两种不同的制动力，并协调三种不同的减速状态，以 同时确保制动性能并提高能源效率，也至关重要。针对基于自动变 速器的混合动力汽车，提出了一种电子制动与再生制动的协同控制 算法，用于在再生制动降挡过程中保持所需的制动力量和驾驶舒适 性（乔等人，2012）。为配备车桥电机的混合动力运动型多用途汽 车开发了差动制动与车辆稳定性控制策略（巴亚尔等人，2012）。

已提出若干适用于具备再生制动能力的混合动力汽车开发与测试的 关键技术。还设计了一种用于配备轮毂电机和摩擦制动器的电动汽 车及混合动力汽车的混合防抱死制动系统（德卡斯特罗等人， 2012）。然而，现有研究中很少涉及电驱动系统动力学及其对再生 制动控制性能的影响。尽管一些研究人员研究了电动汽车的动力总 成系统动力学，但其目标主要是极限驾驶工况下的牵引力控制，或 聚焦于车辆的NVH（噪声、振动和粗糙度）性能（阿曼等人， 2004；尹等人，2009）。

本章旨在对再生效率与乘坐舒适性进行协同优化，针对电驱动 乘用车研究了制动复合控制策略。在MATLAB/Simulink中建立了 包含非线性电驱动系统模型和液压制动系统模型的复合制动系统模 型。通过仿真与实车测试，对控制策略在典型减速过程中的控制效 果和再生效率进行了研究与分析。

277电动汽车的制动协调控制
此外，由于电动动力总成提供的再生制动在系统动力学方面与传统 摩擦制动存在显著差异，因此分析了动力总成非线性（即齿隙和柔 性）对再生减速过程中车辆驾驶性的影响。为了进一步提高制动协 调控制性能，开发了一种具有分层架构的基于模式切换的主动控制 算法，用于补偿齿隙和柔性。所提出的控制算法在再生制动过程中 与基准策略进行了比较。同时给出了一些仿真与实验结果。

8.2 制动协调系统建模

8.2.1 系统概述

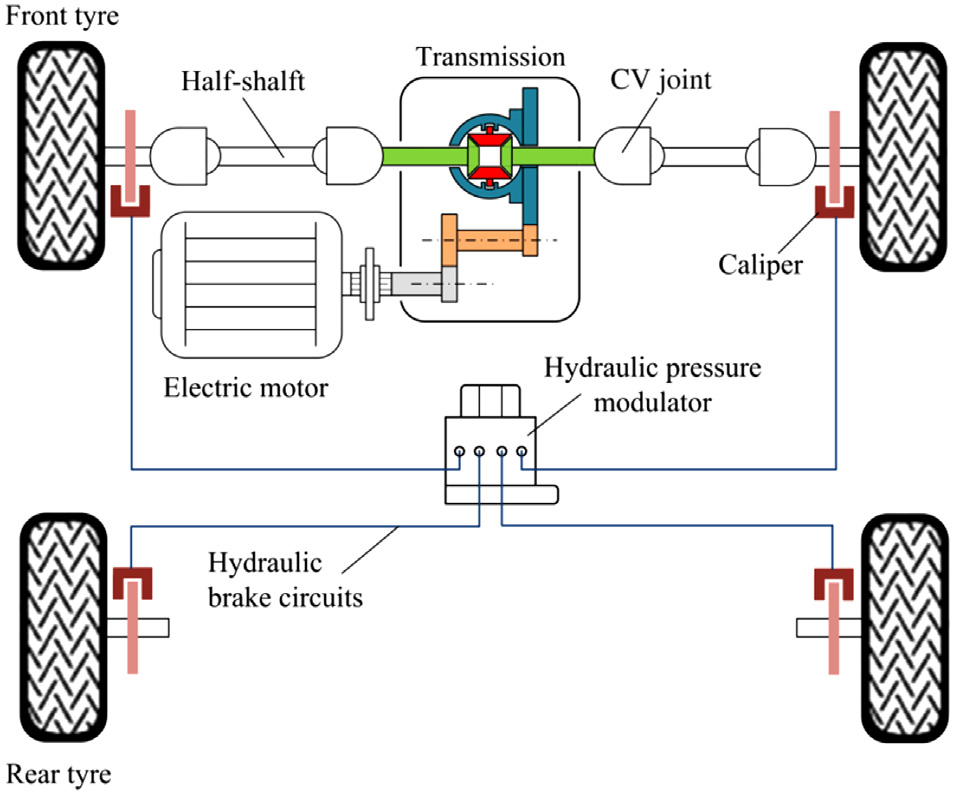
图8.1 展示了本研究中考虑的再生与液压复合制动系统的整体结构。
中央电机安装在车辆的前轴上。在减速过程中，通过传动系统传递 的再生制动力矩作用在车轴上。同时，摩擦制动力矩由液压调节器 进行调节。复合制动力矩实现了整体的制动操作。

8.2.2 电驱动动力总成模型

电动动力总成由电动机、变速箱、主减速器、差速器和半轴组成。
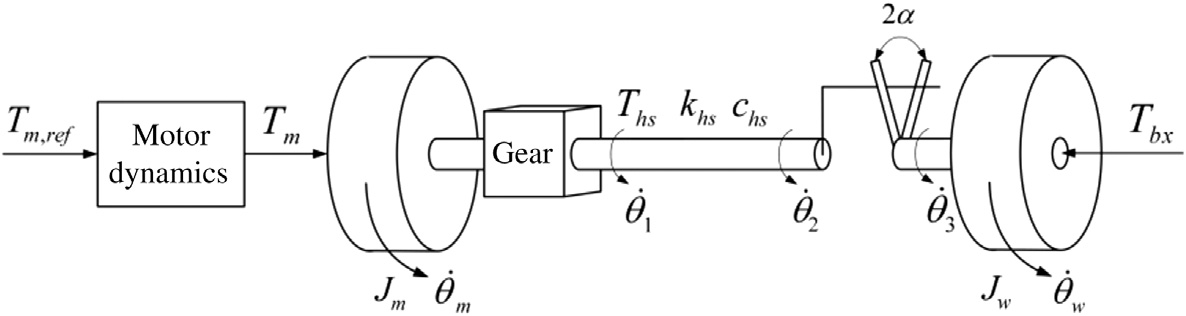
图8.2显示了一个简化的动力总成模型，而本研究中采用的是双惯量 模型。其中一个惯量代表电动机，另一个对应车轮的贡献。变速箱 包括传递、主减速器、差速器以及内外等速万向节，位于电机惯量 附近。整个动力总成中的间隙效应被集中为一个单一的齿隙角 2α。
传动系统的柔性主要假设集中在半轴上，由其刚度和阻尼特性表示。
假设左右半轴长度相同，电机输出转矩被认为平均分配到左右半轴 上。

考虑到电气系统动态特性的影响，电机扭矩被建模为具有小时 间常数的一阶响应 τm（Lvet al., 2015ac），如下所示。
τmT_m1 Tm5 Tm;ref (8.1)
其中Tm是电机扭矩实际值，Tm;ref是参考值。

电机输出轴到半轴的传递扭矩的动态方程如下：
J mθ € m1 bm θ_m5 Tm2 1
i0ig U2Ths (8.2)
其中，Jm为电机惯量，bm为电机粘性摩擦，i0为主减速比，ig为 传动比，Ths为半轴扭矩。

一个带有非线性间隙的柔性半轴连接变速箱和车轮惯性。半轴 扭矩的非线性模型可表示为（Lv等，2015ac）：

Ths5 khsθs1 chsθ_s (8.3)
θs5 θd2 θb (8.4)
θd5 θ12 θ3; θb5 θ22 θ3 (8.5)
其中khs和chs分别为半轴的刚度系数和阻尼系数；θd为轴扭转角； θb为齿隙中的位置；θ1、 θ2和 θ3分别为轴上所示位置的角度，如 图图8.2所示，其中 θ15 θm=i0ig和 θ35 θw。

齿隙位置的非线性模型由Lagerberg和Egardt（2007年）描述：
θ_b5
max 0;θ_d1 khs chs
ðθd2 θbÞ
!
; θb52 α
θ_d1 khs chs
ðθd2 θbÞ ; jθ bj, α
min 0;θ_d1 khs chs
ðθd2 θbÞ
!
; θb5 α 8>>>>>>>>><>>>>>>>>>: (8.6)
其中 2α 是齿隙的大小。

上述公式(8.6)表明， θb只能在间隙范围内变化，而不能超 出边界。当卡在边界时，_轴位移速率θd必须相对于轴扭转足够大， 才能使θb开始向间隙内移动。

驱动轮的动态方程如下：
J wθ € w1 bw θ_w5 Ths2 Thb2 Tbx (8.7)
其中，Jw为车轮惯性，道路负载被分为摩擦项bw和外部轮胎纵向 力Tbx。由机械液压制动装置产生的摩擦制动力矩Thb可被视为对车 轮的扰动。

8.2.3 液压制动系统

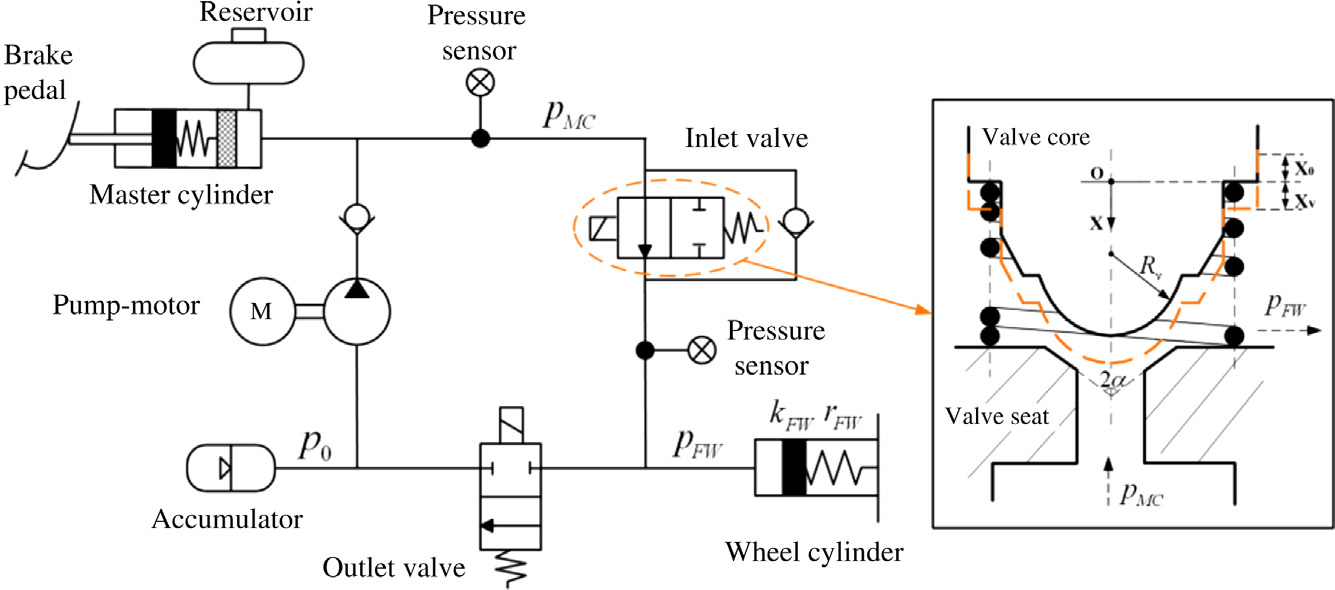
为了模拟和分析制动能量协调性能，建立了包括阀门动态和车轮制 动压力在内的液压制动系统模型。液压制动系统的示意图如图8.3所 示。

8.2.3.1 阀门动力学

在制动压力建立过程中，液压油通过常开型进油阀从主缸流向轮缸。
因此，进油阀模型对于液压制动压力调节的仿真具有重要意义。有 关阀门结构和模型的详细描述已有报道（吕等人，2014ac， 2016年，2017年；张等人，2014a,b）。

进油阀的示意图及其坐标系如图8.3右侧所示。图8.3中给出了 阀芯位置的轴向动力学方程，可表示为：
mvx€v5 Fe2 Fs2 Fh2 FB (8.8)
其中，mv为阀芯的质量，xv为阀芯的位移，Fe为电磁力，Fs为弹 簧力，Fh为液压力，FB为粘滞力。

作用在阀芯上的电磁力可以用以下关系式表示：
Fe5
ðINÞ2
2Rg l (8.9)
其中，I为线圈电流，N为匝数，l为气隙长度，Rg 为空气隙的磁阻。

弹簧力可以由以下关系给出：
Fs5 ksðxv1 x0Þ (8.10)
其中，ks 是回位弹簧的刚度系数，x0 是弹簧的预负载位移。

粘滞力受流体粘度和阀芯运动速度的影响，如公式(8.11)所示。
FB5 Bx_v (8.11)
其中B是粘性阻尼系数。

流体作用在阀芯上的液压力可按以下公式计算（吕等人，2014ac）：
Fh5 πR2 vðcosαÞ2 UΔp2 2Δp C2 dAvcosα2 ρf luidLq_v (8.12)
Av5
πdm Rv
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R2 v2
d2m
4 r Uxv (8.13)
其中，Cd为阀入口流量系数， ρf luid为液压油密度，Rv为阀芯球面 半径，L为阻尼长度，qv为阀的流体流量，Δp为阀两端的压差， dm为阀座平均直径。

8.2.3.2 液压制动压力

轮缸的结构被简化为一个活塞和一个弹簧。基于上述分析的阀门动 态，轮缸压力可以表示为（吕等人，2014ac）：
p_FW5
kFW π2rF4W CdAv
ffiffiffiffiffiffiffiffiffifffifi
2 UΔp
ρ sf luid (8.14)
其中，kFW 是轮缸弹簧刚度，rFW 是轮缸的活塞半径。

8.2.4 车辆与轮胎

本文作者建立了基于八自由度的车辆动力学模型（张等人，2012）。
对于制动研究而言，轮胎模型至关重要，应能够同时模拟轮胎在附 着和滑移状态下的实际行为。本章采用了著名的帕杰卡魔术公式模 型（帕杰卡和巴克，1992）。该模型可准确描述纵向和横向联合滑 移工况下的轮胎行为。

282电动汽车建模、动力学与控制
所开发的详细车辆和轮胎模型已有描述（吕等人，2014ac； 张等人，2012）。这些模型的可行性与有效性已通过硬件在环测试 和车辆测试得到验证。电驱动系统和车辆的关键参数列于表8.1中。

参数	值	Unit
电动机
峰值功率	45	kW
最大扭矩	144	Nm
电压	326	V
容量	66	Ah
电池组
车辆
总质量（m）	1360	kg
轴距（L）	2.50	m
空气阻力系数（CD）	0.32	—
轮胎的名义半径(r)	0.295	m
传动比	7.881	—

8.3 再生制动能量管理策略

8.3.1 制动力分配策略

在传统车辆中，由于制动踏板与制动回路的下游机械连接，前后制 动力分配（BFD）在制动过程中不受调节，而是设定为固定值，该 值由所安装制动装置的参数决定，以避免制动踏板感受液压调节的 影响。然而，对于配备制动协调系统的电动汽车，制动踏板与机械 制动执行器机械解耦，线控制动系统可通过调节前后车轮之间的制 动力来实现理想制动分配。因此，为了实现高再生效率并同时保证 制动安全，需要重新考虑前后制动力分配。

8.3.1.1 前后制动力分配

对于前轮驱动汽车，电机制动扭矩只能施加在前轴上。为了达到最 大再生效率，需要充分利用前轴再生制动力矩。
导致制动力分配接近x轴，在图8.4中所示。但为了保证制动过程 中的稳定性，车辆应具有足够的后轮制动力，这是ECE‐R13法规所 要求的，如公式(8.15)和(8.16)所示（高等人，1999）。
z$ 0:11 0:85ðϕ2 0:2Þ (8.15)
z5 du dt U1 g (8.16)
其中，z表示制动强度， ϕ为路面附着系数，u为车辆纵向速度u。

然而，如果期望获得理想的制动性能，则制动力分配应接近理 想制动力分配，而理想制动力分配远离x轴。当需要理想制动力分 配时，前后轮制动力可表示为（吕等人，2014ac）：
Fμ11 Fμ25 ϕ UG (8.17)
Fμ1 Fμ2
5
b1 ϕ Uhg a2 ϕ Uhg (8.18)
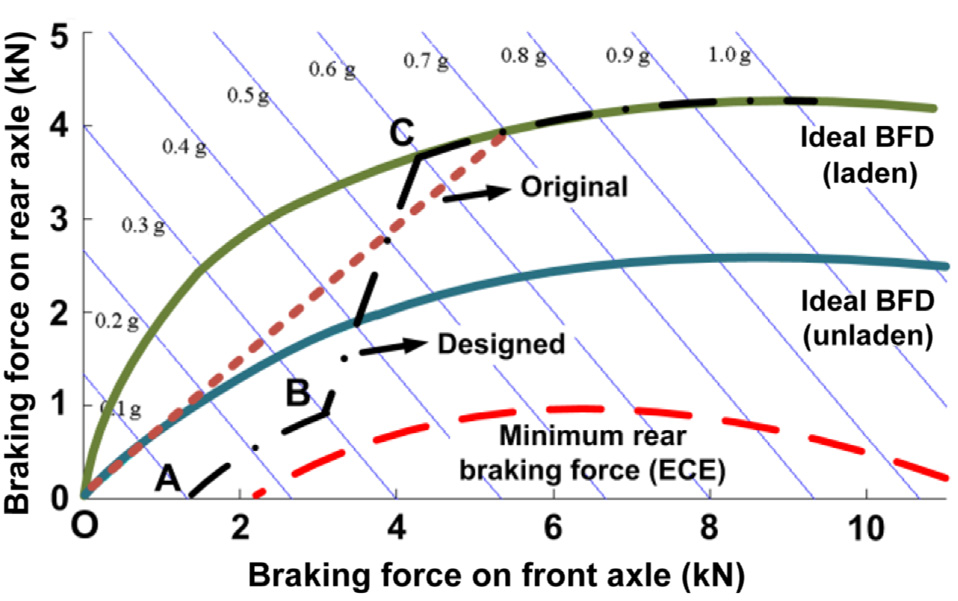
消除变量 ϕ后，前轮制动力与后轮制动力之间的关系可由公 式(8.19)给出。理想制动力分配（满载和空载）如图8.4所示。

Fμ25 1 2 G
hg
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffifffifi
b21 4hg L
G Fμ1 r 2 Gb
hg 1 2Fμ1
” #
(8.19)
其中，Fμ1为前轮制动力，Fμ2为后轮制动力，G为车辆重力，a为 车辆质心到前轴的纵向距离，b为车辆质心到后轴的纵向距离，L为 轴距，hg为质心高度。

因此，根据上述分析可知，在设计前轮驱动电动汽车的前后制 动力分配时，再生效率与制动性能之间存在矛盾。为实现再生效率 最大化的制动力分配与为实现制动性能最大化所要求的制动力分配 相差较大。对于原始策略，制动力分配被设定为一个固定值（张等 人，2012），即前制动力建立与后制动力呈线性关系，如图8.4中 红色虚线所示。然而，这样做无法充分利用再生能力。为解决这一 问题，协调再生效率与制动性能，探索适用于电动汽车的制动力分 配方案具有重要意义。

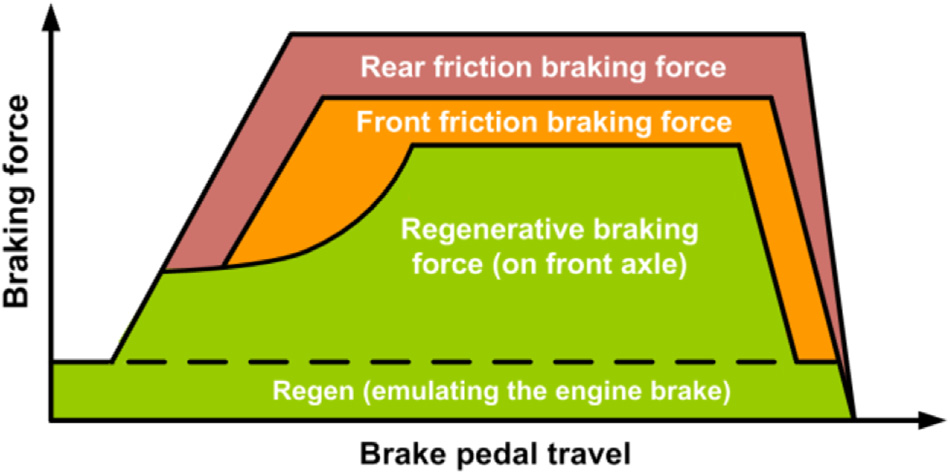
在电动汽车的日常运行工况下，通常需要在正常制动过程中启 用再生制动，对应车辆减速为0.10.3g。一旦进入紧急制动情况 （车辆减速通常大于0.5g），为确保较短的制动距离，车辆需要具 备良好的制动性能。基于这些实际需求，针对前轮驱动电动汽车， 提出以下制动力分配策略：
1. 如图8.4所示，在制动强度较小时，仅施加前轮再生制动力，后 车轴不施加摩擦制动（O到A）；
2. 为了充分保证后轮制动力在 ECE法规规定的限值范围内，从A点开始，线控制动系统逐渐增加 并调节后轮摩擦制动力，直至接近ECE法规要求的限制；
3. 当减速度超过0.3g时，所设计的制动力分配曲线逐渐趋近于理想制动力分 配（B到C），以便车辆在较大制动强度下获得更好的制动性能；
4. 一旦减速度达到0.6g（C点），车辆进入紧急驾驶工况，线控制 动系统将调节前后车轮的液压力，使设计的制动力分配符合理想状态，确 保车辆最佳的动态制动性能。

设计的制动力分配如图8.4中黑色虚线所示。基于上述再生制 动控制策略，目标电动汽车在正常减速过程中可实现高再生效率， 并在紧急制动情况下确保良好的制动稳定性。

8.3.1.2 再生制动与液压制动分配

如图8.5所示，在减速过程中，车辆的总制动力由再生制动与摩擦制 动复合制动提供。总制动力受到控制，并与驾驶员制动意图保持一 致，如公式(8.20)所示。
Tb need5 Treg1 Tf ric (8.20)
其中Tb为车辆的总制动需求，Treg为电动机产生的再生制动力矩，Tf ric表 示机械制动系统提供的摩擦制动力矩。

为了最大化再生效率，在制动协调过程中，前轴将充分利用再 生制动力矩。如图8.5所示，最初仅在前轴施加再生制动。根据控制 算法，一旦电制动无法单独满足制动请求，后轮制动器将由液压制 动系统进行补充。随着驾驶员制动需求的增加，前轴上的液压制动 力随后将被逐渐施加。此外，当车辆进入任何危险驾驶状况时，例如防抱死制 动系统或牵引力控制系统（TCS）启动时，再生制动力矩将逐渐被 取消，即在紧急制动情况下仅由液压制动接管全部制动操作。

8.3.2 混合制动协同控制算法

图8.6 展示了协同再生制动的控制框图。当驾驶员踩下制动踏板时， 可通过踏板单元中的压力传感器检测到总制动需求（Tb need），如 式(8.21) 所示。
Tb need5 4π Uμbr 2 f Re f
β
Up m (8.21)
其中pm为踏板单元的液压缸压力， μb为制动盘的摩擦系数，rf为 前轮轮缸活塞的半径，Re f为制动盘的有效摩擦半径， β为实时前 后制动力分配系数。

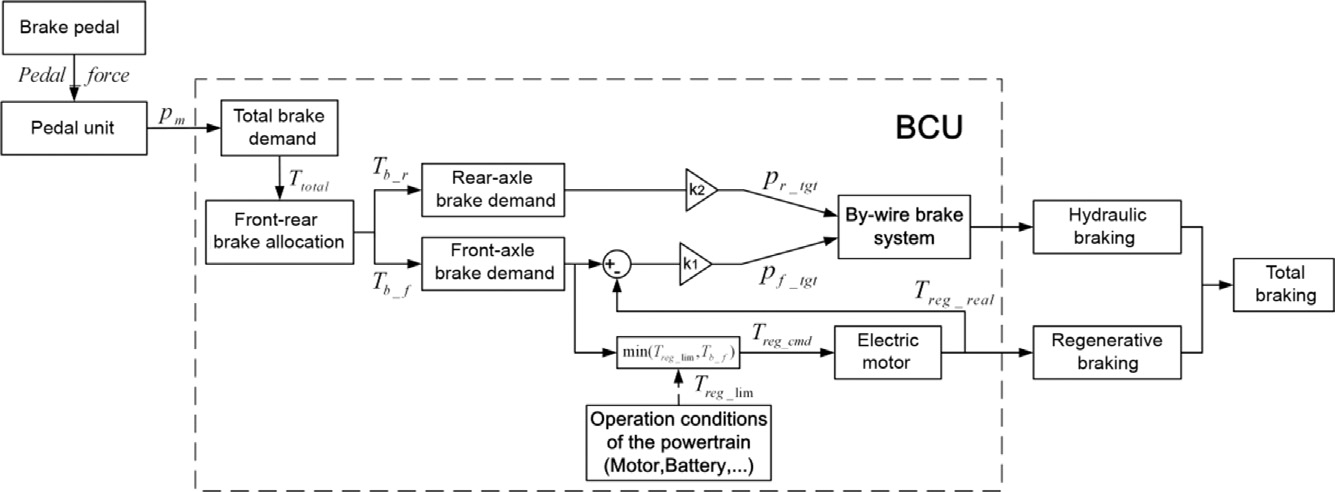
根据车辆的制动需求和设计的制动力分配策略，可以按如下方 式计算前轴制动扭矩（Tb f）和后轴制动扭矩（Tb r）：
Tb f 5 4π Uμbr 2 f Re f Up m (8.22)
Tb r5 Tb need2 Tb f (8.23)

如公式(8.24)所示，根据电池组的荷电状态、电机转速和前轴 的扭矩需求，制动控制单元(BCU)计算再生制动力矩的指令值（ Treg cmd），并通过控制器局域网络(CAN)总线将其发送至电机控制 单元(MCU)。
Treg cmd5 minðTreg lim; Tb f Þ (8.24)
其中Treg lim是电驱动系统可提供的制动扭矩限值。

同时，基于再生制动力矩实际值的反馈信号，可分别计算出前 轮轮缸压力（pf tg t）和后轮轮缸压力（pr tg t）的目标值，如公式 (8.25)和(8.26)所示：
pf tg t5
Tb f 2 Treg real
4πμbr 2 f Re f
(8.25)
p r tg t5
Tb r
4πμbr 2 r Re r
(8.26)
其中rr是后轮轮缸活塞的半径，Re r是后制动盘的有效摩擦半径。

因此，液压制动系统可根据上述计算结果分别调节前后轮轮缸 压力至目标值。最终，电驱动系统提供的再生制动力矩和液压制动 产生的摩擦制动力将满足车辆的总制动需求。

8.3.3 制动能量管理策略的硬件在环仿真

图8.7展示了再生制动控制系统的硬件在环仿真系统的配置。整个 系统由一个实时仿真系统和一个实际制动控制单元组成。实时仿真 系统为dSPACE的AutoBox。虚拟模型，包括车辆动力学、电池、 轮胎和电动机，均嵌入在AutoBox中。制动控制单元是一个实际控 制器，与安装在车辆上的控制器相同。

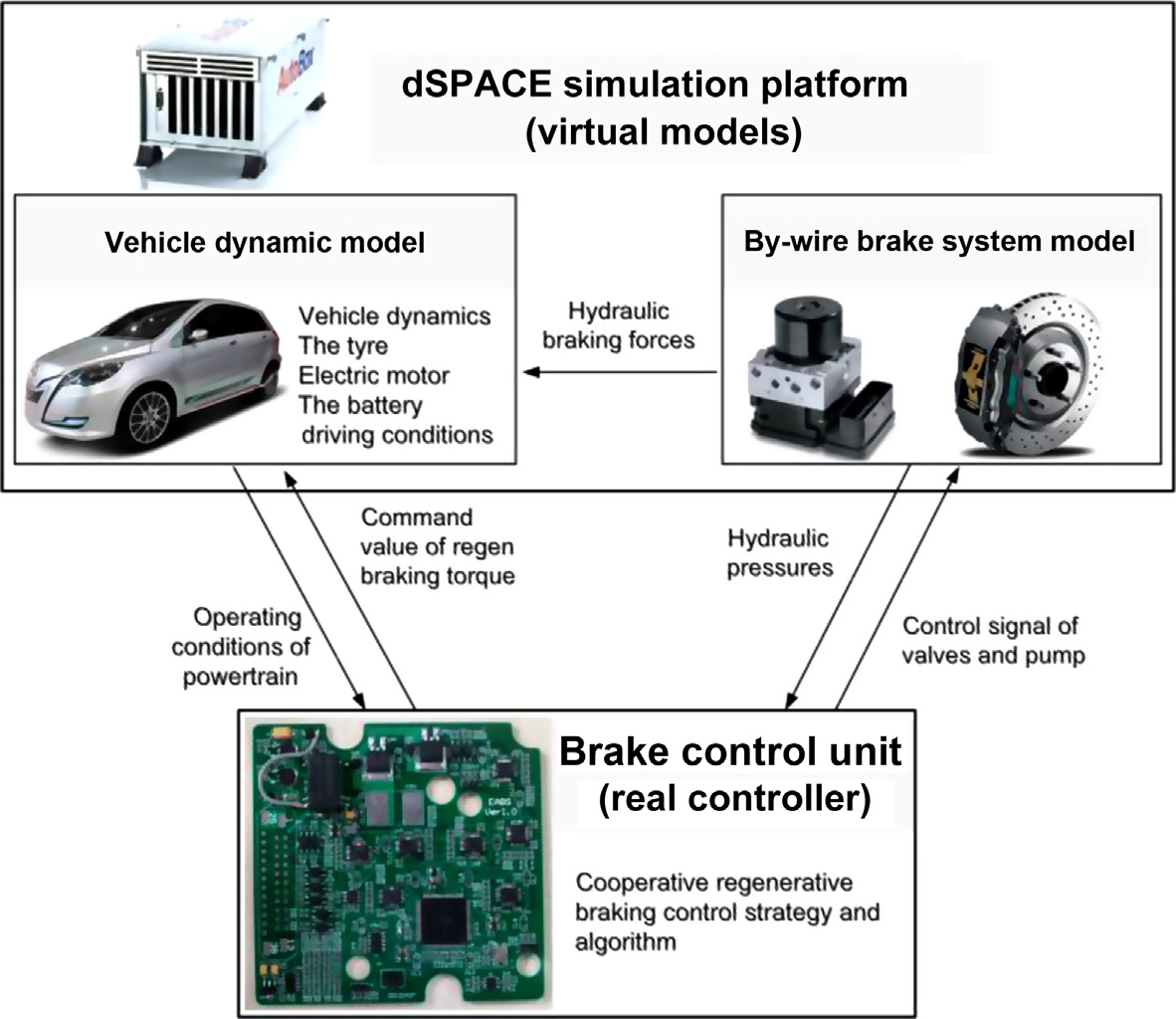
8.3.3.1 硬件在环仿真场景设置

仿真在正常减速过程中进行。在仿真中，初始制动速度设置为30公 里/小时，主缸的制动压力采用斜坡输入并在3兆帕时稳定，路面假 设为具有高附着系数的干燥路面。

以原始制动力分配作为基准策略，比较了基准策略和新提出的 再生制动控制算法在正常制动过程中的再生效率。

8.3.3.2 硬件在环仿真结果与分析

两种不同的再生制动控制策略（即基线策略和提出策略）的仿真结 果如图8.8所示。
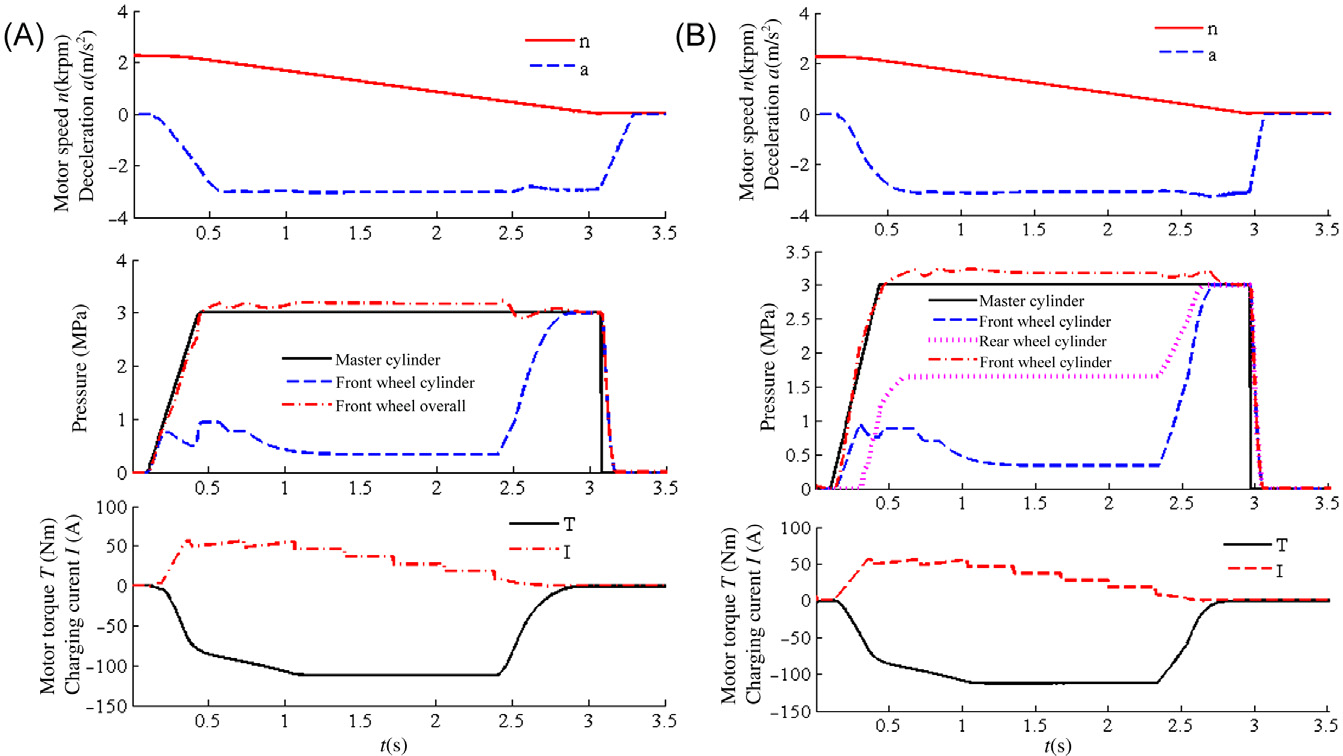基准再生制动控制策略的仿真结果；(B) 提出的再生制动控制算法的仿真 结果)

对于采用原始再生制动控制策略的电动汽车，如图8.8A所示， 由于前后制动力分配设定为固定值，后轮制动压力保持不变与整个制动过程中无任何调节的主缸压力值进行比较。

在提出的再生制动控制策略下，仿真结果如图8.8B所示。在减 速过程开始时，电动机的再生制动力矩逐渐施加到前轴上，前轮制 动压力根据所提出的制动力分配由线控制动系统调节，而后轮制动 器未起作用。0.35秒后，主缸压力达到3MPa，导致车辆的制动需 求相应增加。再生制动与前轴上的机械制动协同工作。同时，后轮 制动力开始由线控制动调节器动态调节，其压力远低于主缸压力， 这是由于所定义的控制策略所致。大约在2.4秒时，车速降低到相对 较低的值。受限于其满载特性，再生制动力矩显著下降。因此，前 液压压力相应增加以满足车辆的制动请求。

前部和后部的液压仍由制动调节器根据提出的分配策略进行调 节。在整个减速过程中，再生制动与摩擦制动相互配合良好，且制动减速度变化平稳，保证了车辆的制动性能。

为了评估所提出的控制算法在再生制动过程中对能量再生性能 的影响，采用再生效率ηreg作为评价参数，表达式为：
ηreg5
Ereg Erecoverable
3 100% (8.27)
其中Ereg为再生制动系统回收的能量，Erecoverable为可回收能量的最大 值，即扣除路面滚动阻力和空气阻力所消耗的能量后剩余的动能。

再生的能量表示为：
Ereg5
ð t1 t0
UIdt (8.28)

通过可回收的能量：
Erecoverable5 1 2 mv22
ð t1 t0
f mgvdt2
ð t1 t0
CD UA 21:15 Uð3:6vÞ2 Uvdt (8.29)
其中，t0为初始制动时间，t1为最终制动时间，U为电池组的输出电压， I为电池的充电电流。

正常制动过程中的再生结果如表8.2所示。根据数据，原始控制 策略的再生效率为64.94%，而所提出的控制算法的再生效率为 80.10%。基于制动耦合系统的所提出的控制算法使再生效率提升了 23%以上。

控制 策略	可回收的 能量 (千瓦时)	再生的 能量 (千瓦时)	再生 效率 (%)	效率 提升 (%)
基线	39.84	25.87	64.94	23.36
提出的	39.98	32.02	80.10
## 8.4 动态制动混合控制算法

将再生制动引入减速操作不仅在提高车辆能源效率方面具有巨大潜 力，也对现有的制动理论和控制方法带来了巨大挑战。在为电动汽 车开发先进的混合制动控制系统时，必须充分考虑动力总成系统的 动态行为。动力总成中有两个主要方面会显著影响车辆的动态性能： 间隙和柔性。它们在扭矩生成与传递的控制回路中引入了强非线性， 导致意外的传动系统振荡（称为抖动；坦普林，2008年）。因此， 在再生减速过程中，动力总成间隙和柔性的补偿对于提升车辆驾驶 性和控制性能至关重要，值得深入研究。

8.4.1 动力总成间隙与柔性对制动协调控制的影响

在现有的复合制动研究中，为了简化控制设计建模，动力总成通常 被建模为刚性系统，忽略了非线性间隙和柔性。因此，半轴扭矩被 视为电机输出扭矩乘以传动比的放大值，而电机扭矩则采用开环控 制。然而，显然在现实世界中存在齿隙非线性和柔性。它们对车辆 驾驶性和再生制动性能的影响将在下文讨论。

8.4.1.1 再生减速期间动力总成间隙对车辆驾驶性的影响

对于电动汽车，如果我们定义当半轴传递驱动力矩时接触为正，则 再生减速期间的接触为负。一旦电动汽车从驱动模式切换到再生制 动模式，间隙被通过，激发了非线性特性。在齿隙（无接触）模式 下，该系统由公式(8.1)–(8.7)描述，可表示为状态空间方程，如公 式(8.30)所示，表明在齿隙中没有扭矩通过半轴传递，且电机与负 载处于解耦状态：

$$
\begin{bmatrix}
\dot{T} m \
\dot{\theta}_s \
\ddot{\theta}_b \
\dot{\omega}_m
\end{bmatrix}
=
\begin{bmatrix}
-\frac{1}{\tau_m} & 0 & 0 & 0 & 0 & 0 \
0 & -\frac{k {hs}}{c_{hs}} & 0 & 0 & 0 & 0 \
\frac{1}{J_m} & 0 & -\frac{b_m}{J_m} & 0 & 0 & 0 \
0 & 0 & 0 & -\frac{b_w}{J_w} & 0 & 0 \
0 & \frac{k_{hs}}{c_{hs}} & \frac{1}{i_0 i_g} & -1 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & -\frac{1}{J_w}
\end{bmatrix}
\begin{bmatrix}
T_m \
\theta_s \
\theta_b \
\omega_m
\end{bmatrix}
+
\begin{bmatrix}
\frac{1}{\tau_m} \
0 \
0 \
0 \
0 \
-\frac{1}{J_w}
\end{bmatrix}
T_{m,\text{ref}}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
0 \
-\frac{1}{J_w}
\end{bmatrix}
T_{hb}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
0 \
-\frac{1}{J_w}
\end{bmatrix}
T_{bx}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
0 \
-\frac{1}{J_w}
\end{bmatrix}
T_l
$$
(8.30)

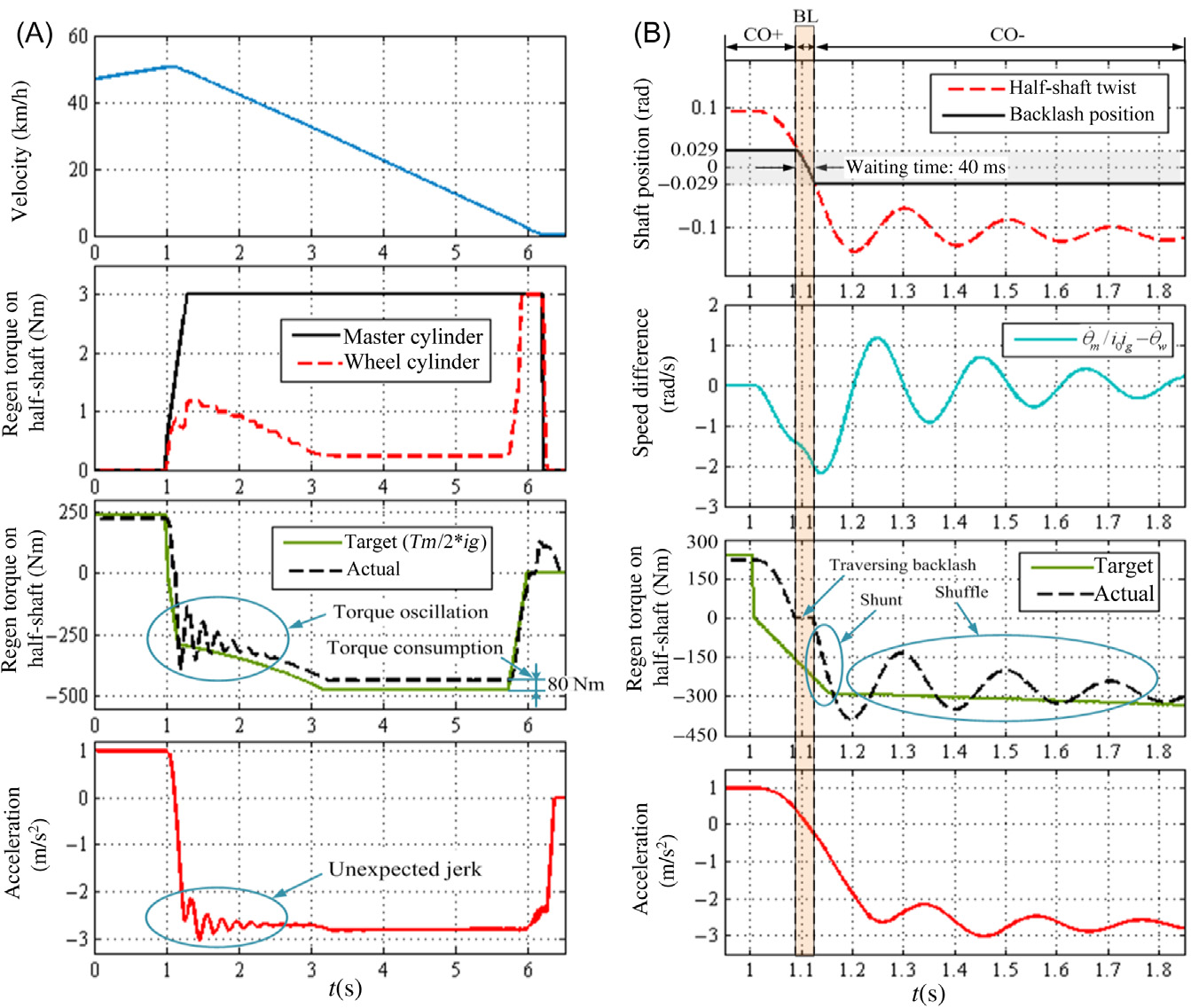
图8.9A 展示了模拟电动汽车的再生制动过程。在最初的一秒内， 车辆处于驱动模式，齿隙处于正接触状态。在1秒时，驾驶员踩下 制动踏板，请求进行减速操作，从而导致电机扭矩由正转负。大约 在1秒时，在切换过程中半轴上出现意外的扭矩振荡，导致车辆减 速时产生不适的冲击。

重点关注图8.9B所示的转矩切换过程，齿隙跨越发生在约1.1秒 处，接触从正侧（CO 1）变为负侧（CO2），持续40毫秒。由于 电机与负载解耦，即半轴扭矩 Ths为零。根据公式(8.2)，在间隙范 围内，所有€电机输出转矩均作用于电机自身的惯性J mθm5 Tm，从而 大幅加速电机。因此，当发生负接触时，电机与负载之间的速度差 超过22弧度/秒。该速度差导致较大的冲击（分流），从而在半轴上 引发转矩振荡（抖动）以及车辆减速过程中意外的顿挫感，这影响 了驾驶性，如子图所示在 图8.9B 中显示。因此，不考虑齿隙跨越的控制器将很难抑制扭 矩振荡。

8.4.1.2 动力总成柔性对制动能量协调性能的影响

柔性主要来源于传动系统的阻尼和弹性特性，尤其是半轴。与仅在 驱动和制动模式切换期间发生的齿隙跨越不同，柔性存在于整个运 行过程（包括牵引和减速）中。如图8.9 所示，在复合制动过程中， 负接触建立后（即处于接触模式时），由于动力总成柔性，半轴扭 矩振荡持续约1秒，然后逐渐减小。此外，扭矩在传递过程中被传动 系统的柔性特性所消耗。

与目标值相比，传动系统在静态下消耗的扭矩达到半轴上的80牛·米。

基于上述现象在时域中的观察，对接触模式下半轴刚度和阻尼 对动力总成动力学特性的影响在频域中进行分析。在接触模式下， 系统状态空间方程重新表述如公式(8.31)所示。状态向量表明，轴 上的扭矩传递得以恢复，电机与负载之间的连接被重新建立。

$$
\begin{bmatrix}
\dot{T} m \
\dot{\theta}_s \
\ddot{\theta}_b \
\dot{\omega}_m
\end{bmatrix}
=
\begin{bmatrix}
-\frac{1}{\tau_m} & 0 & 0 & 0 & 0 & 0 \
0 & -\frac{k {hs}}{c_{hs}} & 0 & 0 & 0 & 0 \
\frac{1}{J_m} & 0 & -\frac{b_m}{J_m} & 0 & 0 & 0 \
0 & 0 & 0 & -\frac{b_w}{J_w} & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
T_m \
\theta_s \
\theta_b \
\omega_m
\end{bmatrix}
+
\begin{bmatrix}
\frac{1}{\tau_m} \
0 \
0 \
0 \
\frac{1}{c_{hs}} \
\frac{1}{c_{hs}}
\end{bmatrix}
T_{m,\text{ref}}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
-\frac{2}{i_0 i_g J_m} \
-\frac{2}{i_0 i_g J_m}
\end{bmatrix}
T_{hb}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
-\frac{1}{J_w} \
\frac{1}{J_w}
\end{bmatrix}
T_{bx}
+
\begin{bmatrix}
0 \
0 \
0 \
0 \
0 \
0
\end{bmatrix}
T_l
$$
(8.31)

根据上述状态空间方程，从电机扭矩到半轴扭矩的传递函数可表 示为：

$$
\frac{T_{hs}}{T_m} = \frac{J_w s^2 + (J_w c_{hs} + b_w k_{hs})s + b_w c_{hs}}{a_1 s^3 + a_2 s^2 + a_3 s + a_4}
$$
(8.32)

where
a₁ = $\frac{1}{i_0 i_g} J_m J_w$;
a₂ = $\frac{1}{i_0 i_g} [J_m(b_w + k_{hs}) + J_w b_m + 2 J_w k_{hs}]$;
a₃ = $\frac{1}{i_0 i_g} [J_m c_{hs} + b_m(b_w + k_{hs}) + 2(J_w c_{hs} + b_w k_{hs})]$;
a₄ = $\frac{c_{hs}}{i_0 i_g} (b_m + 2 b_w)$

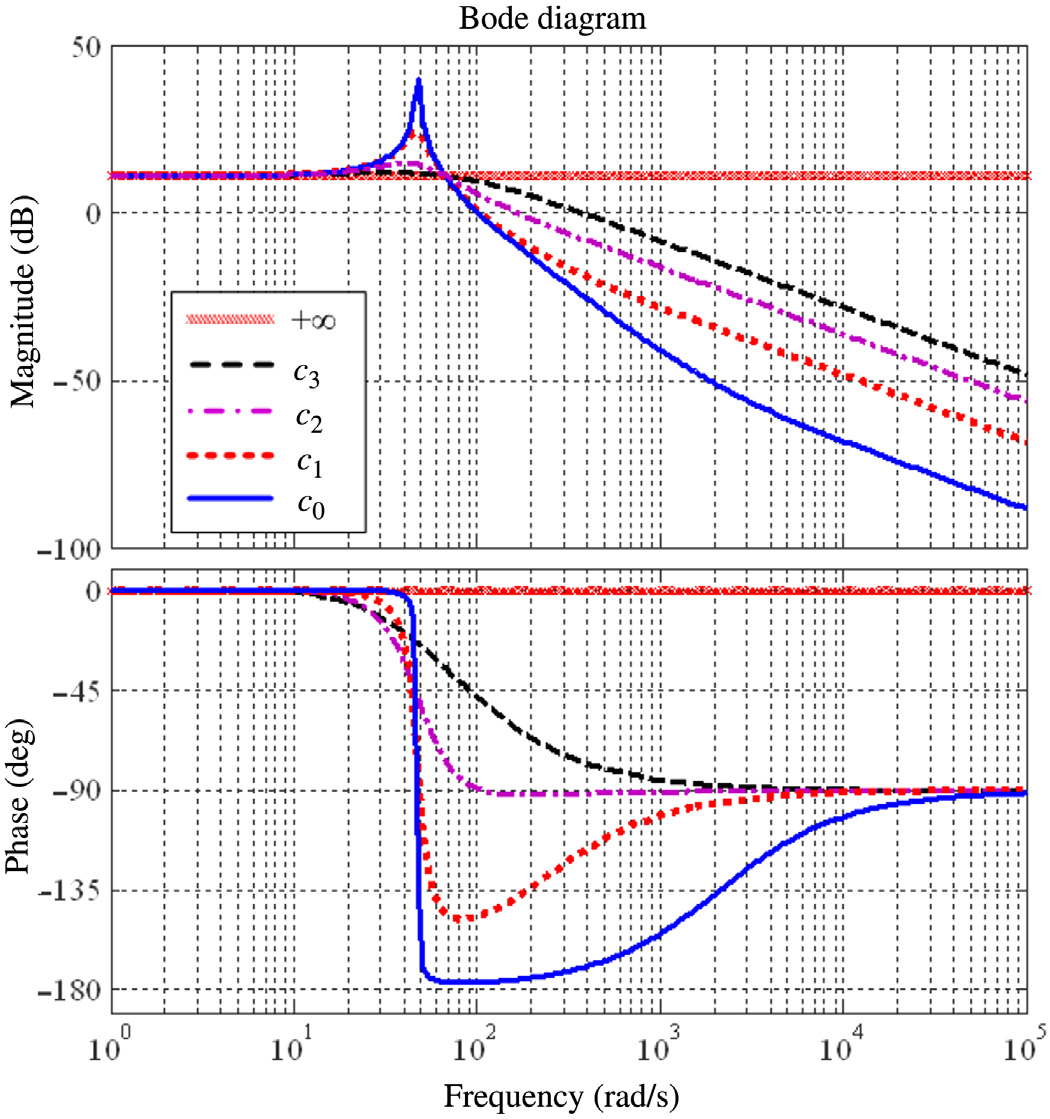
图8.10 显示了基于上述传递函数的半轴扭矩对输入电机扭矩的 伯德图。在低频范围内，传动系统可被视为刚性的。当频率超过 30 rad/s时，负载扭矩的响应表现为一个共振峰。当阻尼系数 chs减 小（c0, c1, c2, c3, 1N）时，在共振点附近，幅值和相位响应均 出现振幅增长。随着频率进一步增加，超过50 弧度/秒时，幅值响应的斜率从 0 逐渐减小到 220 分贝，而相位 值收敛至 290 度，反映了系统的弹性与阻尼特性。

因此，由于其弹性和阻尼特性，电驱动系统不能被简单地视为 刚性的。此外，电动动力总成的开环动态响应无法满足电动汽车先 进控制的要求。

8.4.2 主动动力总成控制算法设计

为了进一步提高电动汽车在复合制动过程中的驾驶性，本节介绍了 一种考虑动力总成间隙非线性和柔性补偿的主动控制算法。

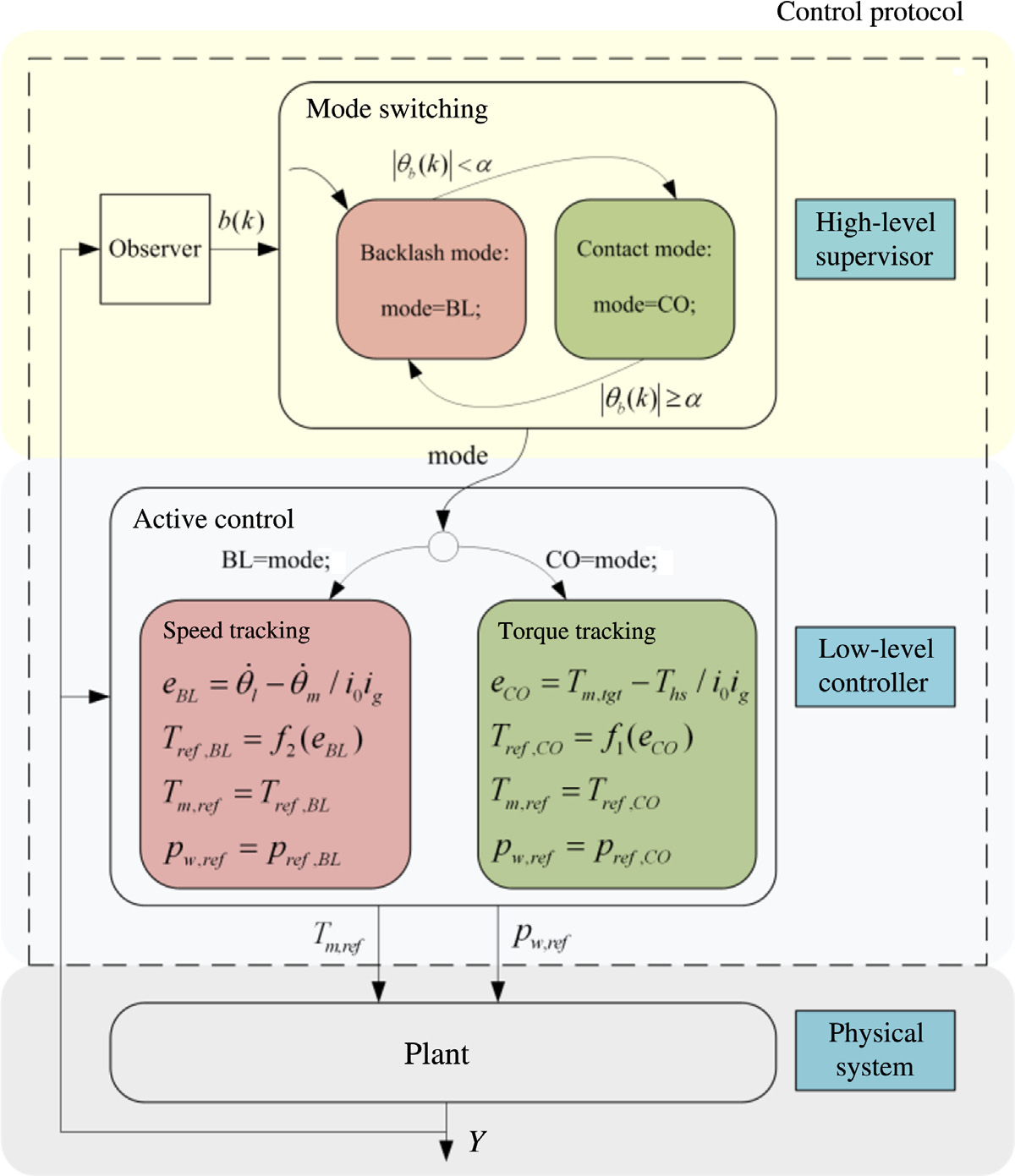
8.4.2.1 分层控制架构

根据上述分析，齿隙控制的明显目标是减小电机在接触重新建立时 对负载的冲击力，实现避免抖振的“软着陆”。这可以通过使速度 差（θw(t) − θm(t)/i₀i_g）保持较小来实现。我们还希望实现具有短时 间延迟的快速过渡，因为等待时间限制了转矩跟踪性能。因此，间 隙补偿可被视为一个速度跟踪问题。控制目标是使电机转速 θm(t)/i₀i_g 跟踪参考速度θref(t)，本研究中该参考速度即为车轮速度 θw(t)。

在接触模式下，柔性补偿主动控制可被视为转矩跟踪问题，而 非回差控制中的速度跟踪。因此，控制目标是通过半轴扭矩 −2Ths(t)/i₀i_g 跟踪目标转矩 Tm,tgt(t)。

根据上述讨论的考虑，开发了一种整体控制协议。该控制协议 采用分层架构，由高层模式切换监控器和低层主动控制器组成，如 图8.11所示。

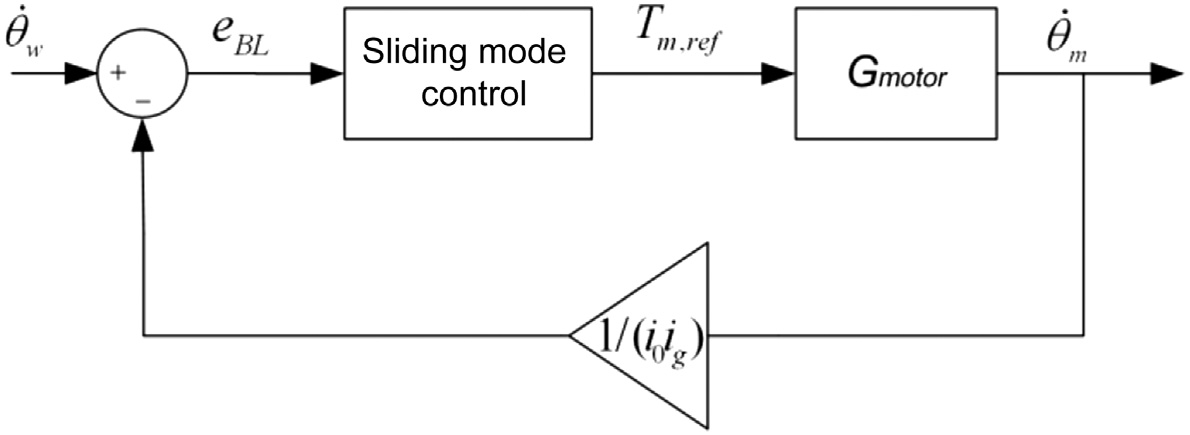
8.4.2.2 基于滑模的动力总成间隙补偿控制器

由于其能够处理非线性问题并实现良好的性能和快速响应，因此采 用了滑模控制(SMC)方案。如上所述，在间隙模式下的目标是通过 电机转速跟踪参考速度，该参考速度由高层监督控制器设定。因此， 误差项定义为：

eBL = θ̇m/i₀i_g − θ̇w (8.33)

设计滑模控制的第一步是定义滑动面。为了保证稳态误差为零， 选择了一种积分型滑动面（宋和赫德里克，2011），如公式(8.34)所示：

S = d/dt + λ ∫e dt (8.34)

其中n是系统阶数， λ是正增益。

基于 公式(8.2)，系统的阶数为一。因此滑动面可以定义如下：

S = eBL + λ∫eBL dt (8.35)

设计一种将系统轨迹引导至滑动面的控制律的方法是李雅普诺 夫直接方法。以下李雅普诺夫函数用于单输入单输出系统：

V = ½ S² (8.36)

为了确保系统的稳定性，李雅普诺夫函数的导数应满足以下条件：

V̇ = SṠ ≤ 0 (8.37)

如果 Ṡ = −KS，其中 K 是正控制增益，则上述不等式可以被 满足。因此，

SṠ = −KS ⇒ S(Ṡ + KS) = 0 (8.38)

根据 公式(8.35)，S的导数可表示为：

Ṡ = θ̈m/i₀i_g − θ̈w + λe (8.39)

为了保证滑模控制系统的稳定性和可达性，正控制增益 K 可 选择为（哈立德，2001年；吕等人，2016年，2017年）：

K ≥ |θ̈w − θ̈m/i₀i_g + λ(θ̇w − θ̇m/i₀i_g)| (8.40)

结合 公式(8.2)和(8.39)，忽略电动机的动态特性，并 将 S 代入 S + KS = 0，得到如下表达式：

θ̈w − (1/(i₀i_g J_m)) Tm,ref + λeBL + KS = 0 (8.41)

因此，间隙模式下的控制输入可写为：

Tm,ref = Tref,BL = i₀i_g J_m(θ̈w + λeBL + KS) (8.42)

事实上，该系统的标准滑模控制律应定义为：

T₀ref,BL = i₀i_g J_m(θ̈w + λeBL + K sgn(S)) (8.43)

sgn(S) =
{
1, S > 0
0, S = 0
−1, S < 0
} (8.44)

然而，众所周知，在标准SMC中，不连续的符号函数sgn(S)在 状态轨迹接近滑动面时可能会引起抖振。为了避免这种现象，上述 不连续项被公式(8.42)中的连续函数KS所替代，从而消除了控制输 入中的抖振（Fazeli等，2012）。

在混合制动过程中，还需要考虑对齿隙控制性能有显著影响的 液压制动。

由于间隙阶段的半轴扭矩为零，根据 公式(8.7)，给定一个稳 定工作点 (Tbx,0; θw,0)，车轮动力学可以表示为：

θ̈w(t) = −(1/J_w) Thb(t) − (1/J_w)(Tbx,0 + b_w θ̇w,0) (8.45)

根据 公式(8.45)，如果 |Thb(t)| < 0，即如果液压制动力矩减小， 车轮减速度将增加，这将导致速度差变大。因此电机需要更大的控 制 effort 来跨越间隙。如果 |Thb(t)| > 0，即如果摩擦制动力矩 增大，尽管相对速度会变小，但再生效率将减弱。考虑最坏情况， 如果摩擦制动过量施加，接触可能会在另一侧重新建立。为了简化实现，在齿隙阶段可以保持摩 擦制动扭矩，即轮缸压力，如公式(8.46)所示。

p_FW,ref(t) = 0 (8.46)

8.4.2.3 用于动力总成柔性补偿的扭矩跟踪控制器

如上所述，在接触模式下，动力总成柔性补偿可被视为一个转矩跟 踪问题。控制目标是跟踪目标转矩Tm,tgt，其中 −2Ths/i₀i_g。采用了一种 组合前馈与反馈控制结构（吕等，2015a–c）：

Tm,ref = Tff + Tfb (8.47)

其中，Tff 是用于跟踪的前馈输入项，Tfb 是为减小控制误差而设计的反馈 分量。

根据控制目标，前馈项可以通过以下方式确定：

Tff = Tm,tgt (8.48)

Tm,tgt = min(|Tb,f|, (1/(i₀i_g)) |Tm,lim|) (8.49)

其中，Tm,tgt为电机扭矩的目标值，Tb,f为前轮的总制动需求，Tm,lim为基于电池荷电状态和电机转速计算得到的电动机转矩限值。

由于在车辆实现中无法通过传感器测量半轴扭矩的值，一些研 究人员已对此进行了估计技术的研究（Bottiglione等人，2012； 阿曼等人，2004）。假设半轴扭矩的值可获取，则半轴扭矩的目标 值与实际值之间的误差项可表示为：

eCO = Tm,tgt − (−2Ths/i₀i_g) (8.50)

对于反馈项，采用线性PID控制律：

Tfb = KP eCO + KI ∫eCO dt + KD d/dt eCO (8.51)

其中反馈增益 KP、KI 和 KD 是调参参数。

因此，在接触模式下，控制输入可以表示为：

Tm,ref = Tref,CO = Tm,tgt + KP eCO + KI ∫eCO dt + KD d/dt eCO (8.52)

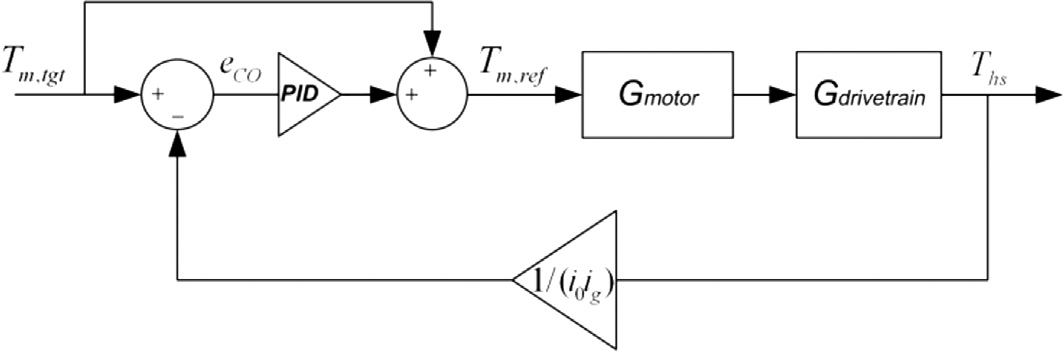
接触模式下用于柔性补偿的扭矩跟踪控制器框图如图8.13所示。

为了满足车辆在接触模式下的整体制动需求，基于前轮的总制 动需求Tb,f和半轴扭矩值Ths，计算得到液压制动压力的参考值，如 式(8.53)所示：

pFW,ref = k₀(Tb,f − 2Ths) (8.53)

其中，k₀ 是轮缸压力与制动扭矩的转换系数，由机械制动装置的 参数确定。

8.4.3 动态制动力协调控制的仿真验证

为了评估所提算法在正常减速过程中的控制性能，在 MATLAB/Simulink中使用第8.2节中描述的模型进行了仿真。第8.2节。

在仿真中，初始制动速度设置为40 km/h。车辆在前1秒内处于 驱动状态，随后驾驶员在1 s时请求制动扭矩。接触状态从CO 1切 换至CO2，同时齿隙被通过。主缸压力采用斜坡输入，稳定在3 MPa。路面假设为无坡度的干燥路面，附着系数为0.8。

传统的开环非主动控制被用作基线。该基线控制的仿真结果如图 8.9所示。

为了说明所开发的主动控制系统的重要性及其在提高控制性能方面 的有效性，进行了仅针对柔性补偿的接触模式主动控制（“接触式 主动”）以及针对柔性和齿隙双重补偿的结合接触和间隙模式的主 动控制（“组合主动”）的仿真。选取纵向加速度值作为评估车辆 驾驶性的参数。以下介绍部分结果。

8.4.3.1 接触模式主动控制仿真结果

图8.14 显示了忽略齿隙影响的接触模式主动控制用于柔性补偿的仿 真结果。根据图8.14，为了补偿传动系统中再生制动扭矩传递过程 中的功率损失，电机扭矩当半轴扭矩增加并在1.4秒开始时确保实际半轴扭矩迅速达到目标值。

然而，由于该控制未涉及齿隙补偿，在齿隙穿越过程中电机与车轮 之间的速度差显著增加，几乎达到23弧度/秒。尽管穿越间隙的等 待时间缩短至38毫秒，但此举导致半轴扭矩出现剧烈振荡，从而在 负接触重新出现初期引发意外的抖动。由于液压制动压力是基于电 机制动力矩进行调节的，因此在1.1至1.4秒期间也出现了不期望的 频率调制。这些结果表明，在先进的电驱动控制系统中实施齿隙补 偿的主动控制是值得的。

8.4.3.2 组合接触和间隙模式下主动控制的仿真结果

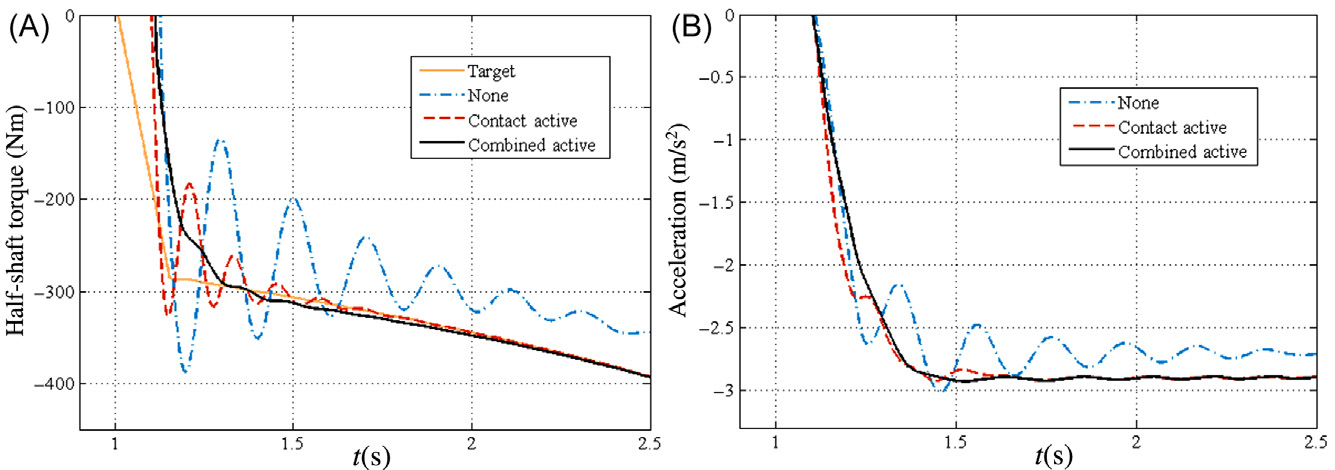
图8.14A 显示了针对柔性和齿隙补偿的主动控制仿真结果。与上述 接触模式主动控制类似，该策略也确保半轴扭矩与目标值保持一致， 以补偿传动系统中的扭矩损失。此外，在齿隙模式期间，激活的滑 模控制器降低了电机扭矩需求，从而减小了电机与车轮之间的速度 差。在间隙控制期间保持液压制动压力，如图8.14B的第三个子图 所示。尽管齿隙跨越的等待时间略微增加至46ms，但半轴扭矩振荡 显著降低。在过渡过程中，电机的再生制动扭矩平稳施加，确保了 舒适的减速过程。

8.4.3.3 三种控制算法的比较

图8.15A表明，这两种主动控制算法在补偿动力总成柔性的同时， 均能确保良好的转矩跟踪性能。组合主动控制策略在切换过程中实 现的齿隙补偿方面优于其他两种策略，从而进一步改善了车辆驾驶 性，如图8.15B所示。

三种控制策略的性能和再生效率也将在下文进行定量比较。为 了对比每种策略的控制性能，通过多种方法对1到2.5秒期间半轴扭 矩的跟踪误差et进行了分析。平均跟踪误差|et|和误差的标准差 σet被选为评价参数。如表8.3所示， 组合主动控制策略在三种策略中表现出最佳的跟踪性能，其对应的 值分别为|et| = 21.05 牛·米 和 σet = 55.31 牛·米。

| 控制算法 | |et| (牛·米) | σet (牛·米) | 回程间隙通过时间 (毫秒) |
| — | — | — | — |
| 基线 | 64.82 | 85.69 | 40 |
| 接触式主动 | 25.50 | 60.25 | 38 |
| 组合主动 | 21.05 | 55.31 | 46 |

三种控制策略的控制性能也在车辆层面进行了比较，如表8.4所 示。所开发的两种主动控制算法在减速和再生效率方面均优于传统 方法。尽管两种改进的控制算法在减速方面的表现几乎相同，但组 合主动控制算法在再生效率方面表现更优。

控制 算法	平均减速度 (m/s²)	均方根 加加速度 (m/s³)	再生 效率 (%)
基线	2.75	10.35	64.68
接触 激活	2.96	3.46	67.52
组合 激活	2.96	3.38	67.71

8.5 结论

为了进一步探索电动汽车制动能量回收潜力和制动性能，研究了制 动协调控制算法。

介绍了所采用系统的布局。在MATLAB/Simulink中建立了与 目标电动乘用车再生制动和摩擦制动相关的主要部件模型。阐述了 提出的再生制动控制算法。通过硬件在环仿真，对所提出的控制策 略的控制效果和再生效率进行了仿真，并与原始控制策略进行了对 比。硬件在环（HiL）仿真结果表明，所提出的再生制动控制算法 在再生效率方面具有优势。原始控制策略的再生效率为64.94%， 而所提出的控制算法的再生效率达到80.10%。基于线控制动系统的 所提出控制算法使再生效率提升了23%以上。

为了改善车辆在再生制动减速过程中的驾驶性，讨论了动力总 成针对齿隙和柔性的主动控制。分析了非线性齿隙和动力总成柔性 对再生制动减速过程中车辆驾驶性的影响。为进一步提高驾驶性和 混合制动性能，开发了一种基于模式切换的主动控制算法，并在正 常减速过程中进行了仿真。仿真结果表明，在组合主动控制下，半 轴扭矩的平均跟踪误差和车辆抖动的均方根分别为21.05 牛·米和 3.38 米/秒³,，验证了所提算法的可行性和有效性。