二叉树:
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->_left = node2;
node1->_right = node4;
node2->_left = node3;
node4->_left = node5;
node4->_right = node6;
return node1;
}
1 二叉树的前、中、后序遍历
1.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
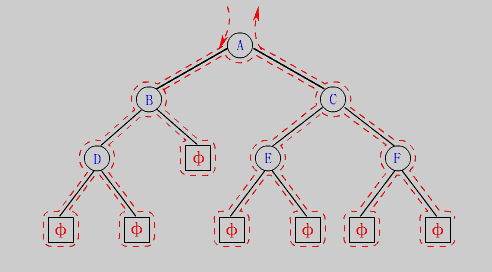
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void preOrder(BTNode* root);
// 二叉树中序遍历
void inOrder(BTNode* root);
// 二叉树后序遍历
void postOrder(BTNode* root);
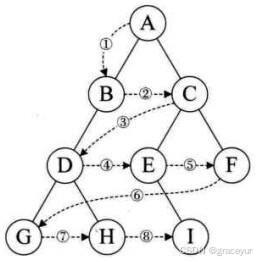
1.2 前序遍历递归图解
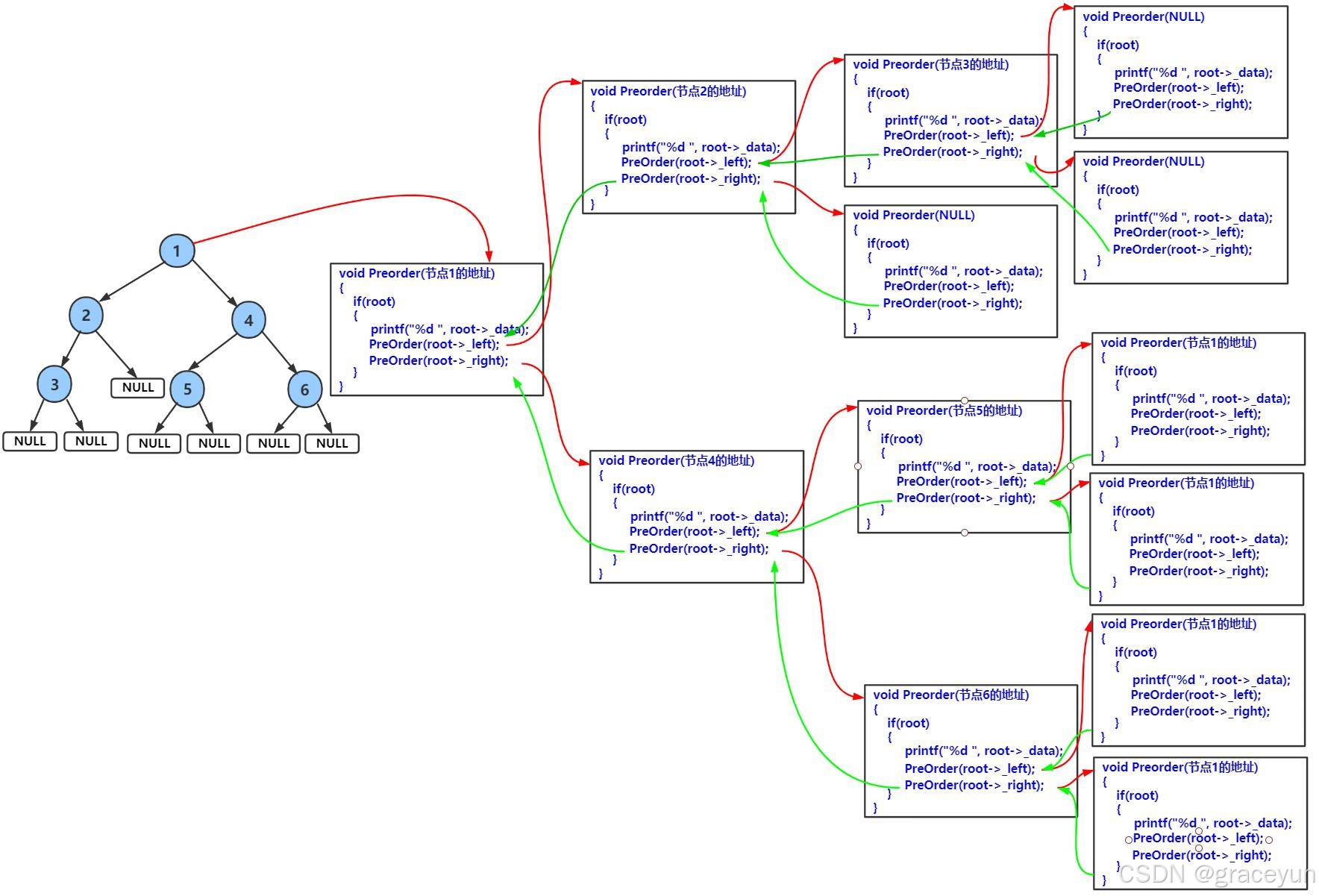
1.3 前序遍历递归调用函数图解
图中二叉树
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 1 5 6 4 1
中序和后序调用和前序的递归调用差不多,只是访问顺序不同,此处不再赘述。
1.3 前中后序遍历代码实现
1.3.0 创建一个固定的二叉树
- 思路:写死一个固定二叉树,申请空间,然后手动指向左右子树
创建二叉树就是这个样子的
- 创建二叉树代码实现
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->_data = x;
node->_left = NULL;
node->_right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->_left = node2;
node1->_right = node4;
node2->_left = node3;
node4->_left = node5;
node4->_right = node6;
return node1;
}
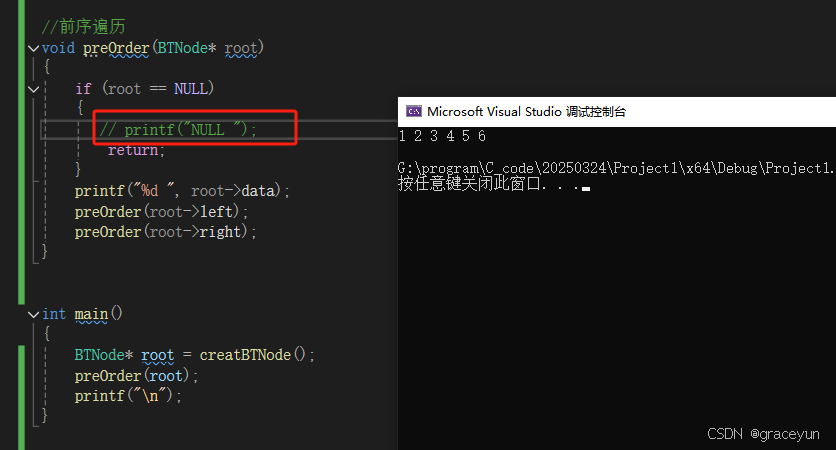
1.3.1 前序遍历
前序遍历是 :根 左 右
二叉树的前序遍历结果实际是:1 2 3 MULL NULL NULL 45 NULL NULL 6 NUL NULL
我们不打印NULL就是:1 2 3 4 5 6
- 前序遍历代码实现
//前序
void preOrder(BTNode * root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->_data);
preOrder(root->_left);
preOrder(root->_right);
}
- 前序遍历代码验证1
- 前序遍历代码验证2
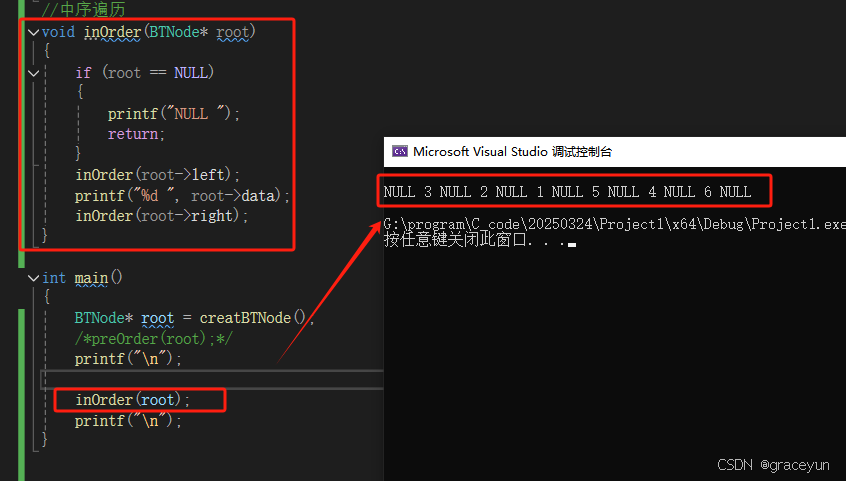
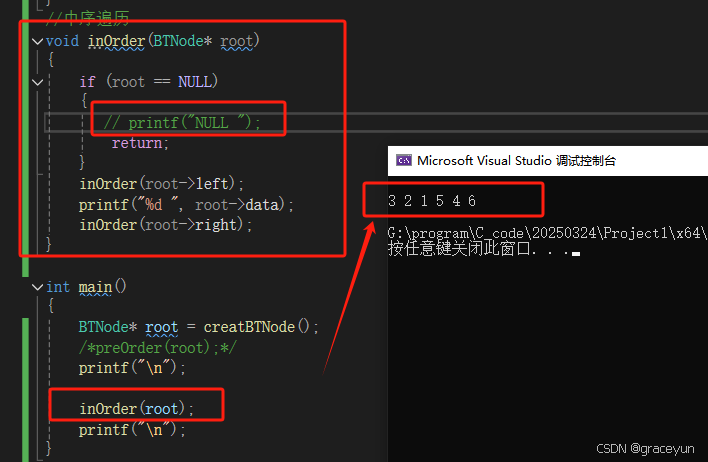
1.3.2 中序遍历
前序遍历是 : 左 根 右
二叉树的前序遍历结果实际是:NULL 3NULL 2 NL 1NLL 5 NULL 4 NULL 6 NULL
我们不打印NULL就是:3 2 1 5 4 6
//中序遍历
void inOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
inOrder(root->left);
printf("%d ", root->data);
inOrder(root->right);
}
- 中序遍历代码验证1
- 中序遍历代码验证2
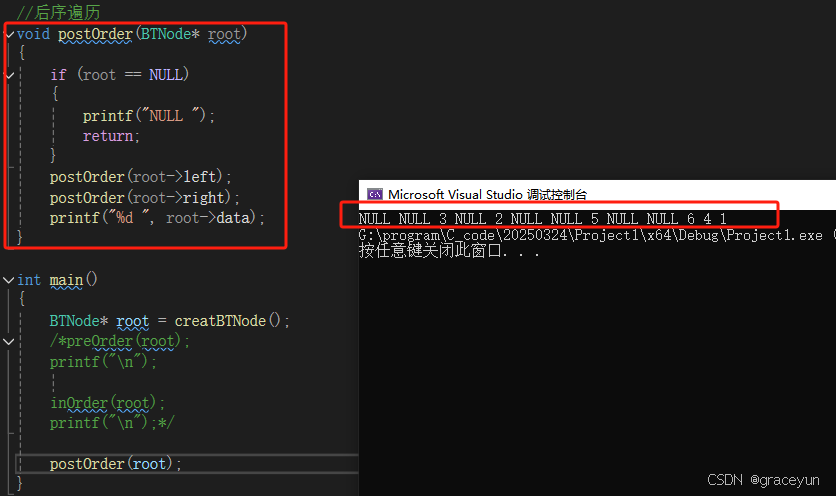
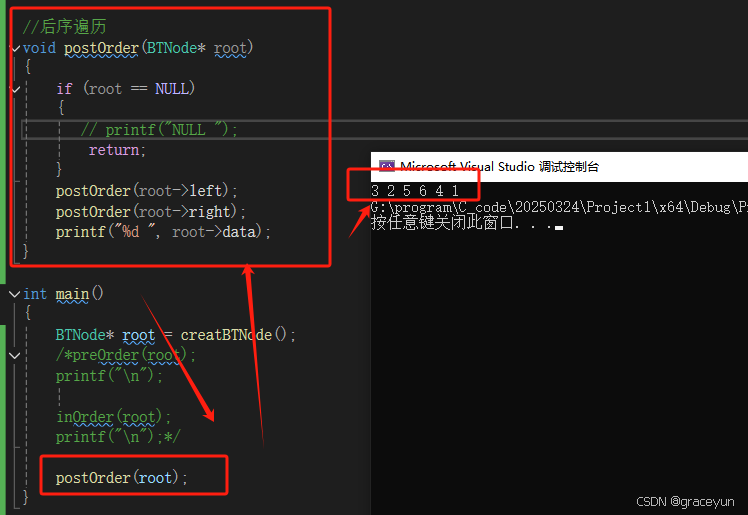
1.3.3 后序遍历
前序遍历是 : 左 右 根
二叉树的前序遍历结果实际是:NULL NULL 3MLL2NULL NULL5 NULL NULL 6 4 1
我们不打印NULL就是:3 2 5 6 4 1
//后序遍历
void postOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%d ", root->data);
}
- 后序遍历代码验证1
- 后序遍历代码验证2
2 节点个数以及高度等函数实现
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
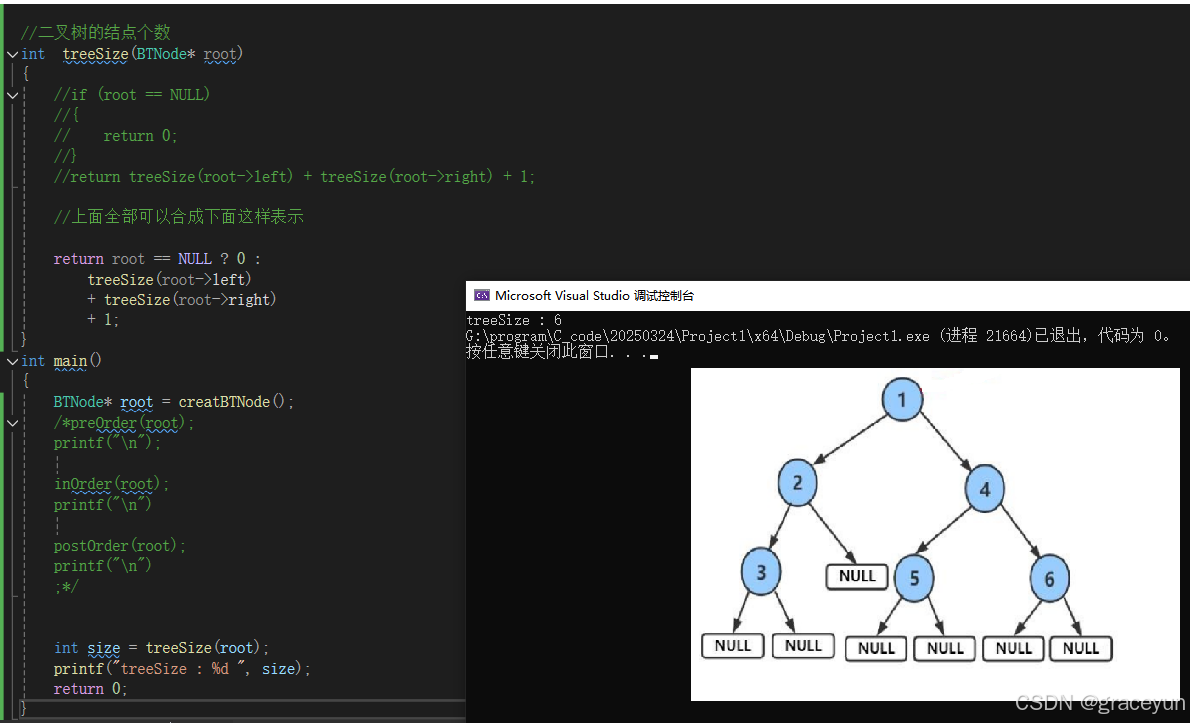
2.1 求二叉树的结点个数
- 求二叉树结点个数思路
采用分治的思想。二叉树的结点个数等于左子树的个数+右子树的个数,最后再加根节点1
代码实现
int TreeSize(BTNode* root)
{
//if (root == NULL)
//{
// return 0;
//}
//return treeSize(root->left) + treeSize(root->right) + 1;
//上面全部可以合成下面这样表示
return root == NULL ? 0 :
TreeSize(root->left)
+ TreeSize(root->right)
+ 1;
}
- 验证
int main()
{
BTNode* root = creatBTNode();
int size = treeSize(root);
printf("treeSize : %d ", size);
return 0;
}
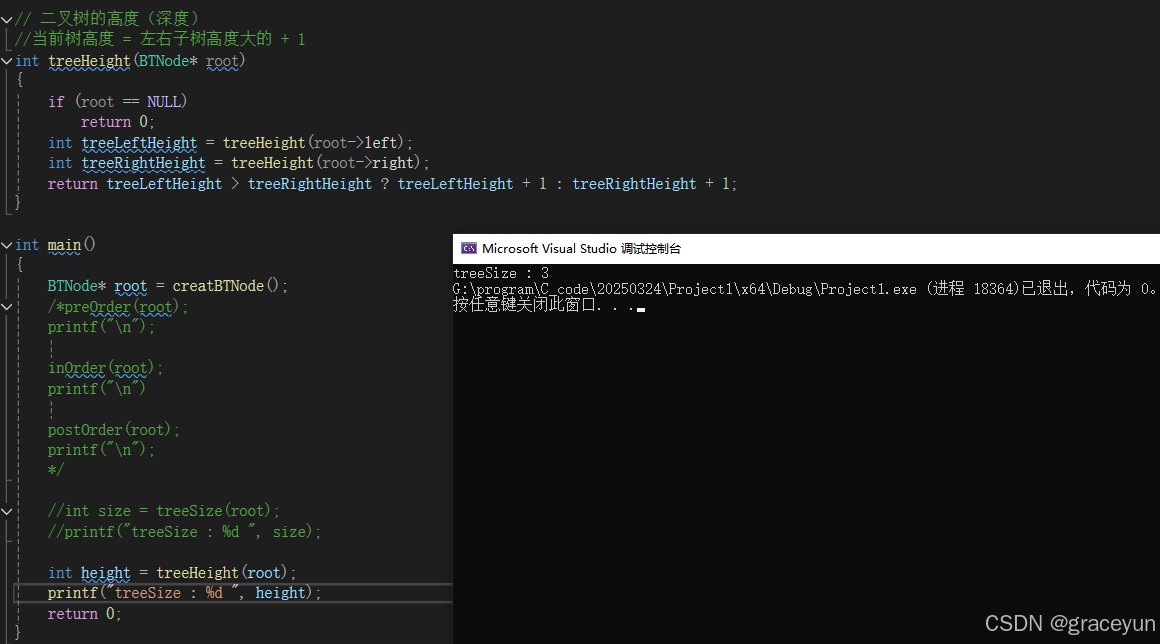
2.2 求二叉树的高度
// 二叉树的高度(深度)
//当前树高度 = 左右子树高度大的 + 1
int treeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int treeLeftHeight = treeHeight(root->left);
int treeRightHeight = treeHeight(root->right);
return treeLeftHeight > treeRightHeight ? treeLeftHeight + 1 : treeRightHeight + 1;
}
- 代码验证
int main()
{
BTNode* root = creatBTNode();
int height = treeHeight(root);
printf("treeSize : %d ", height);
return 0;
}
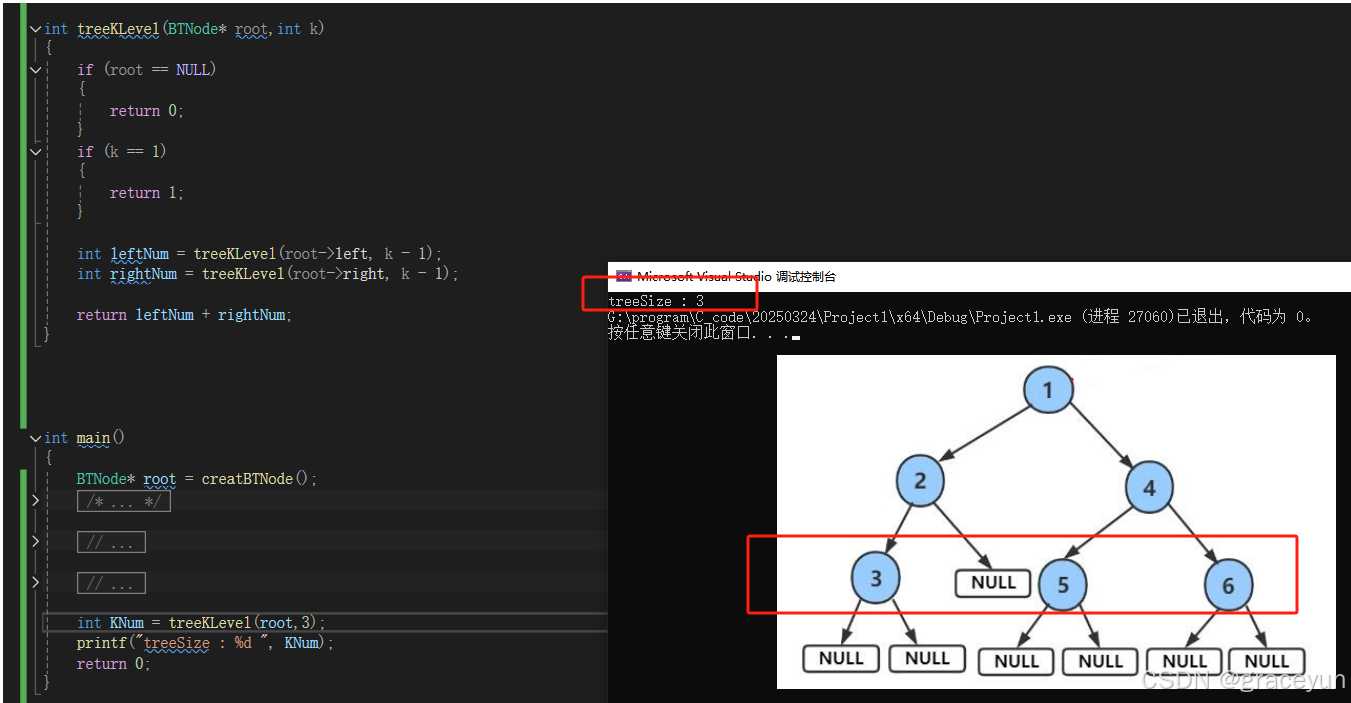
2.3 求二叉树第k层的结点个数
- 思路
当前树的第k层个数 =左子树的第k-1层个数 +左子树的第k-1层个数
- 代码实现
int treeKLevel(BTNode* root,int k)
{
if (root == NULL)
{
return 0;
}
int leftNum = treeKLevel(root->left, k - 1);
int rightNum = treeKLevel(root->right, k - 1);
return leftNum + rightNum;
}
- 验证
int main()
{
BTNode* root = creatBTNode();
int KNum = treeKLevel(root,3);
printf("treeSize : %d ", KNum);
return 0;
}
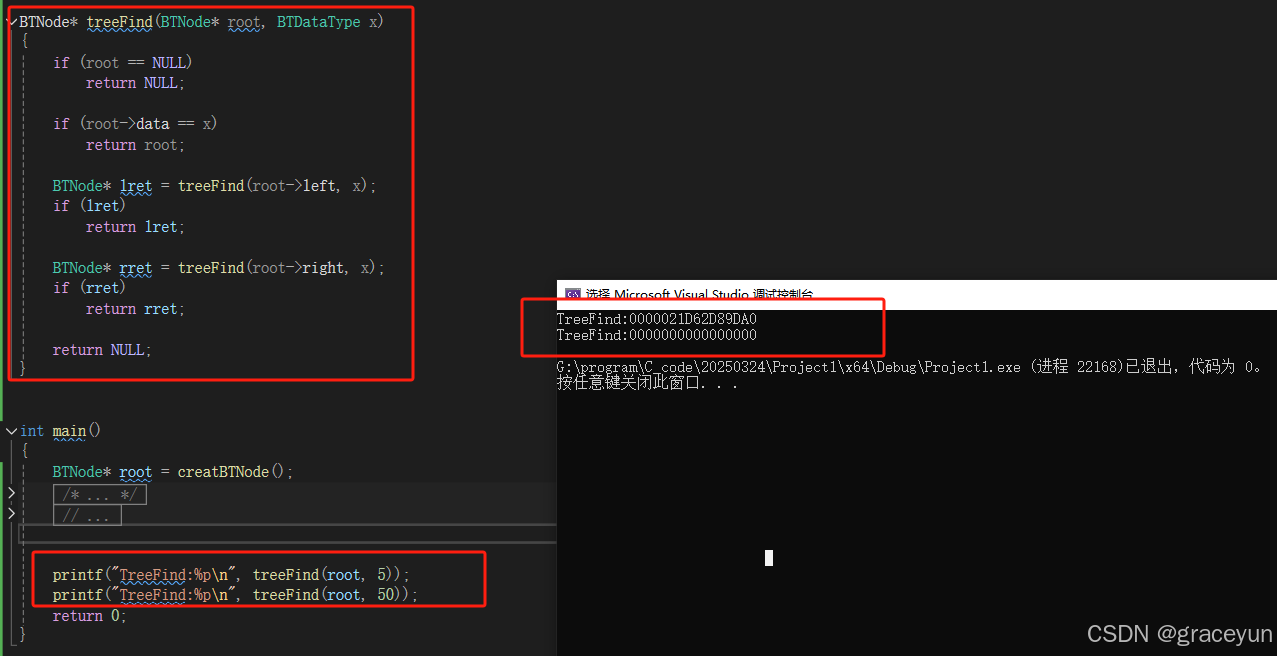
2.4 二叉树查找值为x的节点
BTNode* treeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* lret = treeFind(root->left, x);
if (lret)
return lret;
BTNode* rret = treeFind(root->right, x);
if (rret)
return rret;
return NULL;
}
- 代码验证
int main()
{
BTNode* root = creatBTNode();
int KNum = treeKLevel(root,3);
printf("treeSize : %d ", KNum);
return 0;
}
3. 层序遍历
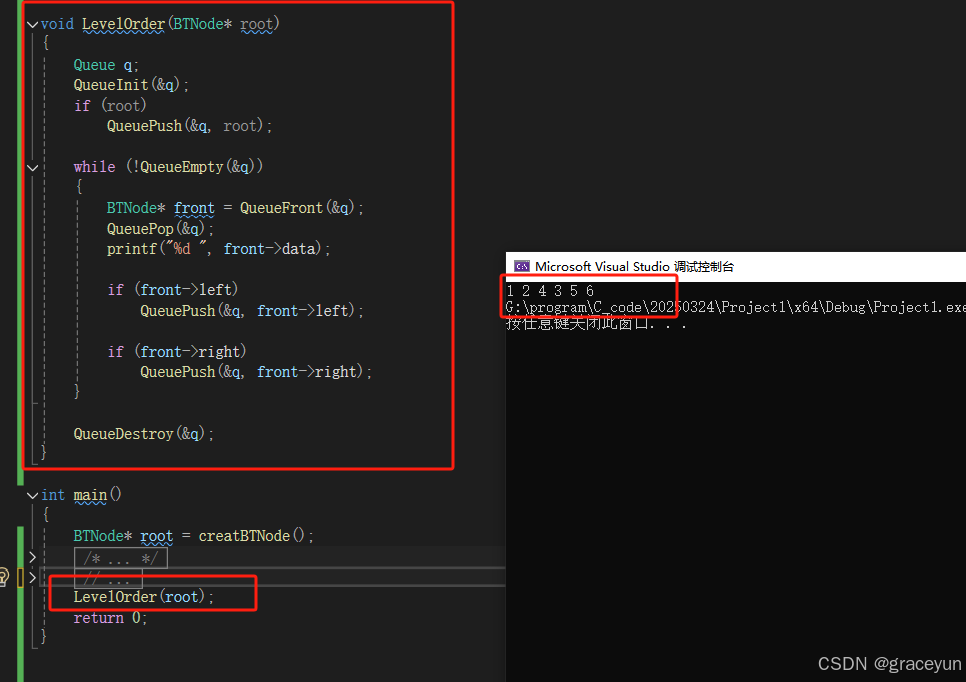
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
3.1 层序遍历代码实现
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->_data);
if (front->_left)
QueuePush(&q, front->_left);
if (front->_right)
QueuePush(&q, front->_right);
}
QueueDestroy(&q);
}
3.2 层序遍历代码验证
int main()
{
BTNode* root = creatBTNode();
LevelOrder(root);
return 0;
}
4. 附录 源代码
4.1 test.c 文件
#define _CRT_SECURE_NO_WARNINGS 1
#include"20250324Queue.h"
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* buyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail!");
return NULL;
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
BTNode* creatBTNode()
{
BTNode* node1 = buyNode(1);
BTNode* node2 = buyNode(2);
BTNode* node3 = buyNode(3);
BTNode* node4 = buyNode(4);
BTNode* node5 = buyNode(5);
BTNode* node6 = buyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
//前序遍历
void preOrder(BTNode* root)
{
if (root == NULL)
{
// printf("NULL ");
return;
}
printf("%d ", root->data);
preOrder(root->left);
preOrder(root->right);
}
//中序遍历
void inOrder(BTNode* root)
{
if (root == NULL)
{
// printf("NULL ");
return;
}
inOrder(root->left);
printf("%d ", root->data);
inOrder(root->right);
}
//后序遍历
void postOrder(BTNode* root)
{
if (root == NULL)
{
// printf("NULL ");
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%d ", root->data);
}
//二叉树的结点个数
int treeSize(BTNode* root)
{
//if (root == NULL)
//{
// return 0;
//}
//return treeSize(root->left) + treeSize(root->right) + 1;
//上面全部可以合成下面这样表示
return root == NULL ? 0 :
treeSize(root->left)
+ treeSize(root->right)
+ 1;
}
// 二叉树的高度(深度)
//当前树高度 = 左右子树高度大的 + 1
int treeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int treeLeftHeight = treeHeight(root->left);
int treeRightHeight = treeHeight(root->right);
return treeLeftHeight > treeRightHeight ? treeLeftHeight + 1 : treeRightHeight + 1;
}
int treeKLevel(BTNode* root,int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
int leftNum = treeKLevel(root->left, k - 1);
int rightNum = treeKLevel(root->right, k - 1);
return leftNum + rightNum;
}
BTNode* treeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* lret = treeFind(root->left, x);
if (lret)
return lret;
BTNode* rret = treeFind(root->right, x);
if (rret)
return rret;
return NULL;
}
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
QueueDestroy(&q);
}
int main()
{
BTNode* root = creatBTNode();
/*preOrder(root);
printf("\n");
inOrder(root);
printf("\n")
postOrder(root);
printf("\n");
*/
//int size = treeSize(root);
//printf("treeSize : %d ", size);
//int height = treeHeight(root);
//printf("treeSize : %d ", height);
//int KNum = treeKLevel(root,3);
//printf("treeSize : %d ", KNum);
//printf("TreeFind:%p\n", treeFind(root, 5));
//printf("TreeFind:%p\n", treeFind(root, 50));
LevelOrder(root);
return 0;
}
4.1 Queue.h文件
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef struct BinaryTreeNode* QDatatype;
typedef struct QueueNode
{
struct QueueNode* next;
QDatatype data;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Queue;
void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);
QDatatype QueueFront(Queue* pq);
QDatatype QueueBack(Queue* pq);
4.3 Queue.c文件
#include"20250324Queue.h"
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QDatatype x)
{
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->data = x;
newnode->next = NULL;
if (pq->head == NULL)
{
assert(pq->tail == NULL);
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
void QueuePop(Queue* pq)
{
assert(pq);
assert(pq->head != NULL);
/*QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
if (pq->head == NULL)
pq->tail = NULL;*/
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
pq->size--;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->size == 0;
}
QDatatype QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
QDatatype QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
























 36万+
36万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








