SVM在软间隔数据上的推广
到这里,我们已经了解了线性SVC的基本原理,以及SVM如何被推广到非线性情况下,还了解了核函数的选择和应用。但实际上,我们依然没有完全了解SVM用于二分类的全貌。我们之前在理论推导中使用的数据都有一个特点,那就是他们或是完全线性可分,或者是非线性的数据。在我们对比核函数时,实际上用到了一种不同的数据,那就是不完全线性可分的数据集。比如说如下数据集:
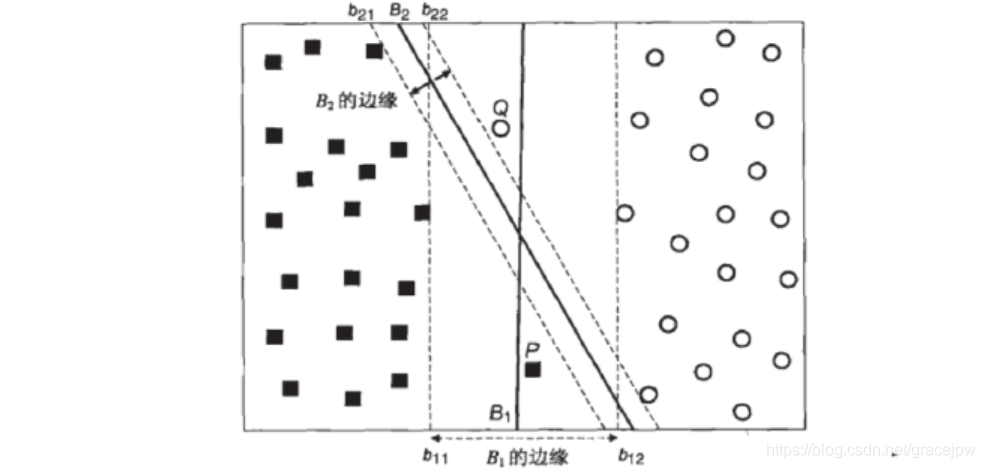
这个数据集和我们最开始介绍SVM如何工作的时候的数据集一模一样,除了多了P和Q两个点。我们注意到,虽然决策边界B1的间隔已经非常宽了,然而点P和Q依然被分错了类别,相反,边际比较小的B2却正确地分出了点P和Q的类别。这里并不是说B2此时此刻就是一条更好的边界了,与之前的论述一致,如果我们引入更多的训练数据,或引入测试数据, 更加宽敞的边界可以帮助它有更好的表现。但是,和之前不一样,现在让边际最大的决策边界的训练误差也不可能为0了。此时,我们就需要引入“软间隔”的概念:
硬间隔与软间隔
当两组数据是完全线性可分,我们可以找出一个决策边界使得训练集上的分类误差为0,这两种数据就被称为是存在”硬间隔“的。当两组数据几乎是完全线性可分的,但决策边界在训练集上存在较小的训练误差,这两种数据就被称为是存在”软间隔“。
我们可以通过调整我们对决策边界的定义,将硬间隔时得出的数学结论推广到软间隔的情况上,让决策边界能够忍受一小部分训练误差。这个时候,我们的决策边界就不是单纯地寻求最大边际了,因为对于软间隔地数据来说,边际越大被分错的样本也就会越多,因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。
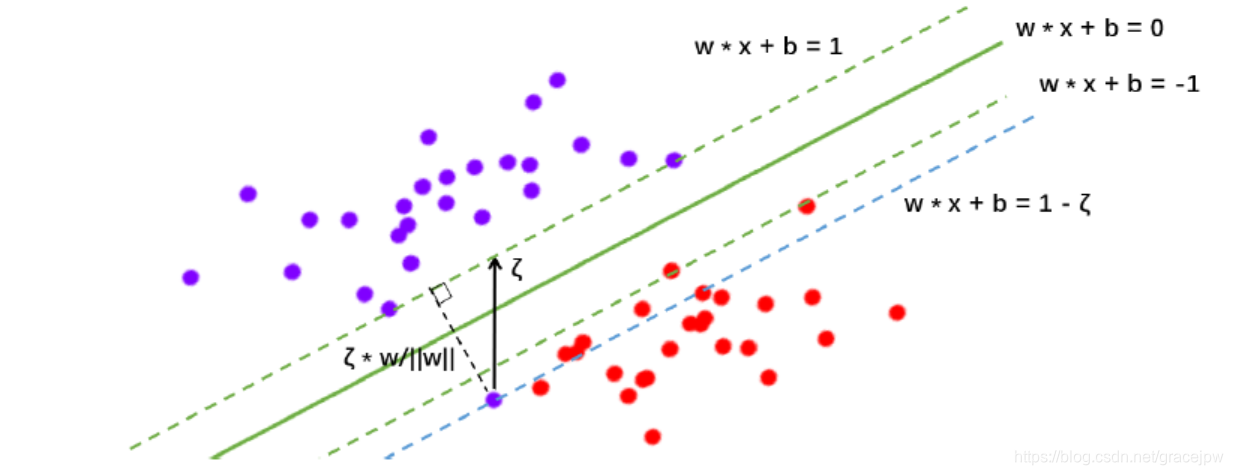
看上图,原始的决策边界ω⋅x+b=0\boldsymbol{ω\cdot x}+b=0ω⋅x+b=0,原本的平行于决策边界的两个虚线超平面ω⋅x+b=1\boldsymbol{ω\cdot x}+b=1ω⋅x+b=1和ω⋅x+b=−1\boldsymbol{ω\cdot x}+b=-1ω⋅x+b=−1都依然有效。我们的原始判别函数为:
ω⋅xi+b⩾1ifyi=1ω⋅xi+b⩽−1ifyi=−1\boldsymbol{ω\cdot x_i}+b\geqslant 1 \qquad if \quad y_i=1 \\
\boldsymbol{ω\cdot x_i}+b\leqslant -1 \qquad if \quad y_i=-1ω⋅xi+b⩾1ifyi=1ω⋅xi+b⩽−1ifyi=−1
不过,这些超平面现在无法让数据上的训练误差等于0了,因为此时存在了一个混杂在红色点中的紫色点xp。于是,我们需要放松我们原始判别函数中的不等条件,来让决策边界能够适用于我们的异常点,引入松弛系数ζ来帮助我们优化原始的判别函数:
ω⋅xi+b⩾1−ζiifyi=1ω⋅xi+b⩽−1+ζiifyi=−1\boldsymbol{ω\cdot x_i}+b\geqslant 1-ζ_i \qquad if \quad y_i=1 \\
\boldsymbol{ω\cdot x_i}+b\leqslant -1+ζ_i \qquad if \quad y_i=-1ω⋅xi+b⩾1−ζiifyi=1ω⋅xi+b⩽−1+ζiifyi=−1
其中ζi>0。可以看得出,这其实是将原本的虚线超平面向图像的上方和下方平移。松弛系数其实很好理解,来看上面的图像。位于红色点附近的紫色点xp在原本的判别函数中必定会被分为红色,所以一定会被判断错。现在作一条与决策边界平行且过点xp的直线ω⋅xi+b=1−ζi\boldsymbol{ω\cdot x_i}+b = 1-ζ_iω⋅xi+b=1−ζi(图中的蓝色虚线)。这条直线是由ω⋅xi+b=1\boldsymbol{ω\cdot x_i}+b = 1ω⋅xi+b=1平移得到,所以两条直线在纵坐标上的差异就是ζ(竖直的黑色箭头)。而点xp到ω⋅xi+b=1\boldsymbol{ω\cdot x_i}+b = 1ω⋅xi+b=1的距离就可以表示为ζ⋅ω∣∣ω∣∣\frac{ζ \cdot ω}{||ω||}∣∣ω∣∣ζ⋅ω,即ζ在ω方向上的投影。 由于单位向量是固定的,所以ζ可以作为点xp在原始的决策边界上的分类错误的程度的表示,隔得越远,分得越错。但注意, ζ并不是点到决策超平面的距离本身。
不难注意到,我们让ω⋅xi+b⩾1−ζi\boldsymbol{ω\cdot x_i}+b\geqslant 1-ζ_iω⋅xi+b⩾1−ζi作为我们的新决策超平面,此时此刻,混杂在红色点中的紫色点就是我们的支持向量了。所以软间隔让决定两条虚线超平面的支持向量可能是来自于同一个类别的样本点,而硬间隔的两条虚线超平面必须是由来自两个不同类别的支持向量决定的。而所有可能影响我们的超平面的样本可能都会被定义为支持向量,此时此刻,支持向量就不再是所有压在虚线超平面上的点,而是所有可能影响我们的超平面的位置的那些混杂在彼此的类别中的点了。观察一下我们对不同数据集分类时,支持向量都有哪些?软间隔如何影响了超平面和支持向量,就一目了然了。
这个新的超平面还有其他的问题,虽然我们把异常的紫色点分类正确了,但我们同时也分错了一系列红色的点。所以我们必须在我们求解最大边际的损失函数中加上一个惩罚项,用来惩罚我们具有巨大松弛系数的决策超平面。我们的拉格朗日函数,拉格朗日对偶函数,也因此都被松弛系数改变。现在,我们的损失函数为:
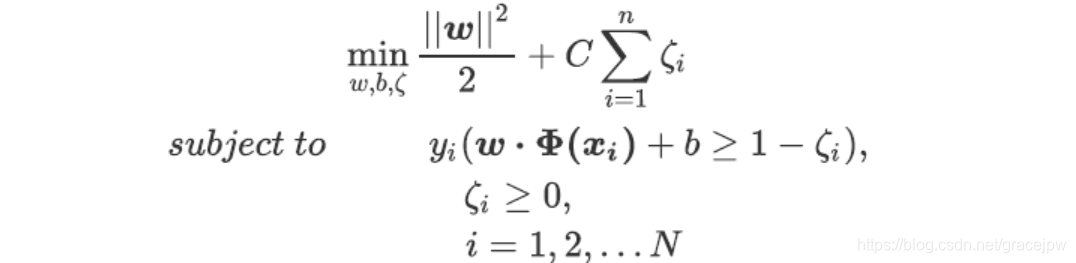
其中C是用来控制惩罚项的惩罚力度的系数。
我们的拉格朗日函数为(其中μ是第二个拉格朗日乘数):
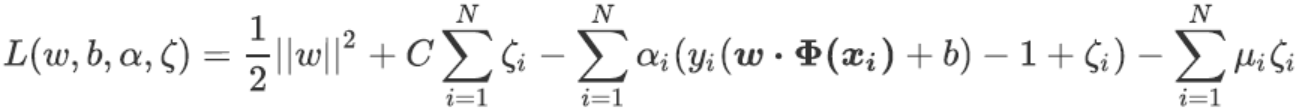
需要满足的KKT条件为:
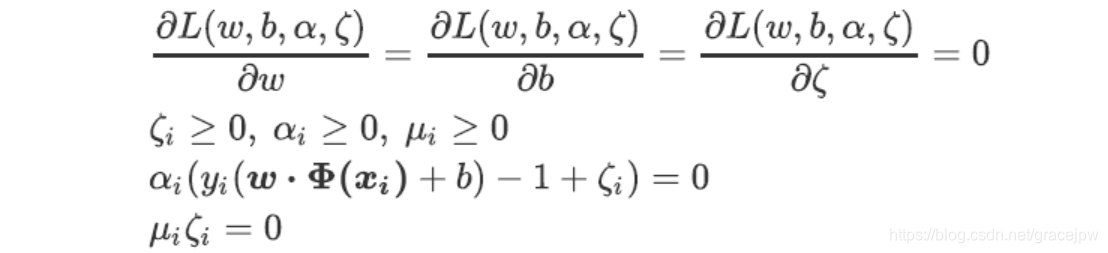
拉格朗日对偶函数为:
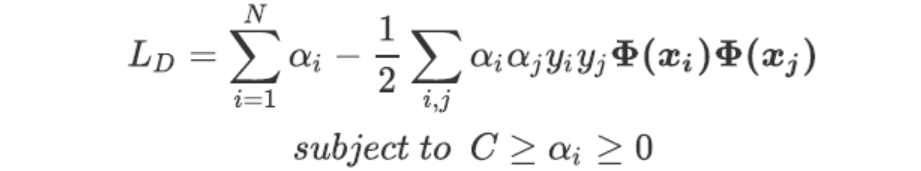
这种状况下的拉格朗日对偶函数看起来和线性可分状况下的对偶函数一模一样,但是需要注意的是,在这个函数中,拉格朗日乘数α的取值的限制改变了。在硬间隔的状况下,拉格朗日乘数值需要大于等于0,而现在α被要求不能够大于用来控制惩罚项的惩罚力度的系数C。有了对偶函数之后,我们的求解过程和硬间隔下的步骤一致。以上所有的公式,是以线性硬间隔数据为基础,考虑了软间隔存在的情况和数据是非线性的状况而得来的。而这些公式,就是sklearn类SVC背后使用的最终公式。公式中现在唯一的新变量,松弛系数的惩罚力度C,由我们的参数C来进行控制。
重要参数C
**参数C用于权衡”训练样本的正确分类“与”决策函数的边际最大化“**两个不可同时完成的目标,希望找出一个平衡点来让模型的效果最佳。
C的含义
浮点数,默认1,必须大于等于0,可不填
C是松弛系数的惩罚项系数。如果C值设定比较大,那SVC可能会选择边际较小的,能够更好地分类所有训练点的决策边界,不过模型的训练时间也会更长。如果C的设定值较小,那SVC会尽量最大化边界,决策功能会更简单,但代价是训练的准确度。换句话说,C在SVM中的影响就像正则化参数对逻辑回归的影响。
在实际使用中,C和核函数的相关参数(gamma,degree等等)们搭配,往往是SVM调参的重点。与gamma不同,C没有在对偶函数中出现,并且是明确了调参目标的,所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1,通常来说这都是一个合理的参数。 如果我们的数据很嘈杂,那我们往往减小C。当然,我们也可以使用网格搜索或者学习曲线来调整C的值。
#参数 C 的学习曲线
#调线性核函数
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="linear",C=i).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
0.9766081871345029 1.2340816326530613
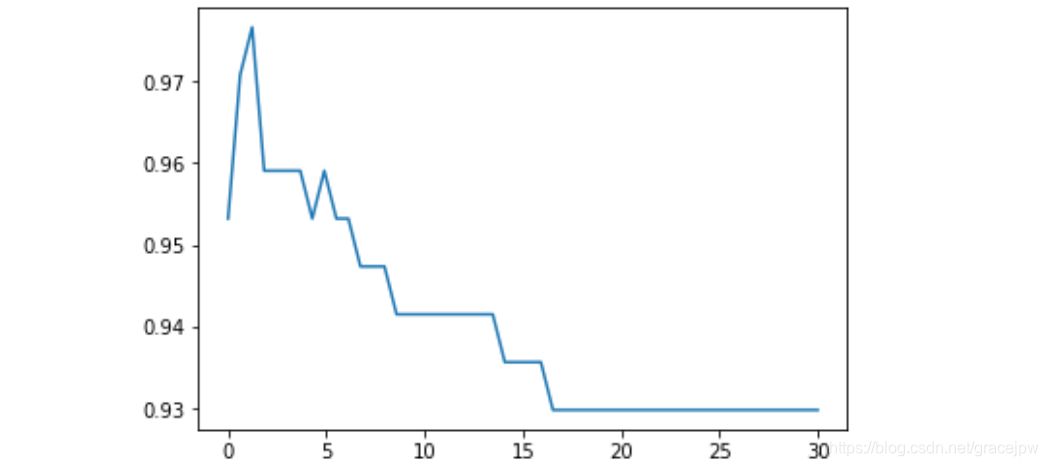
#换rbf
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma = 0.012).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
0.9824561403508771 6.7424489795918365
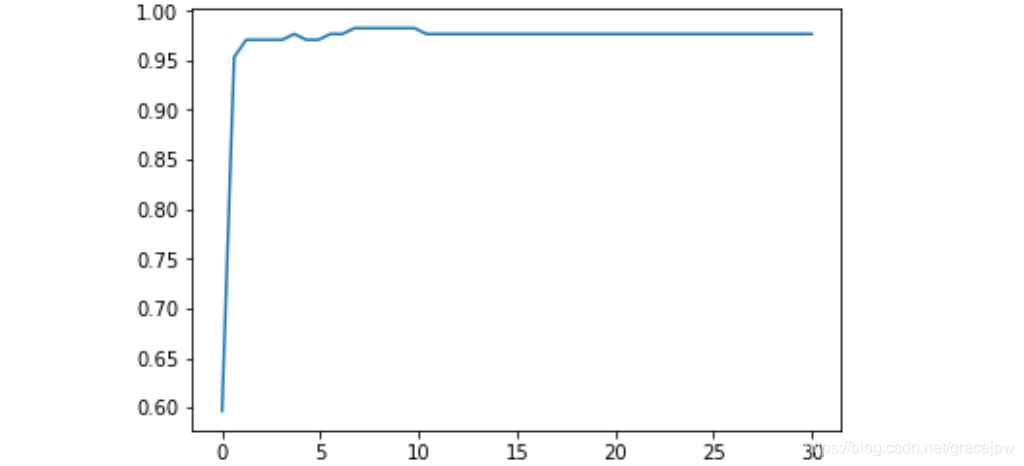
#进一步细化
score = []
C_range = np.linspace(5,7,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma = 0.012).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
0.9824561403508771 6.26530612244898
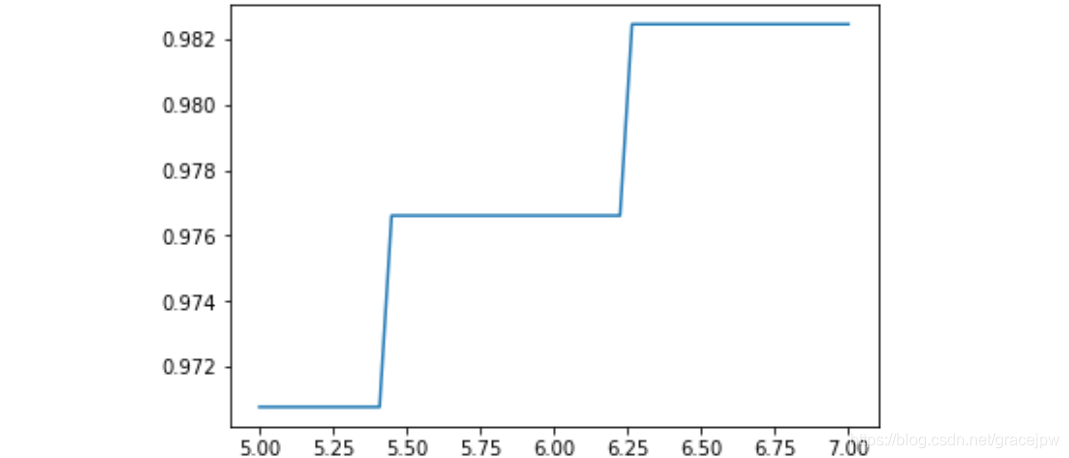
此时,我们找到了乳腺癌数据集上的最优解:rbf核函数下的98.24%的准确率。当然,我们还可以使用交叉验证来改进我们的模型,获得不同测试集和训练集上的交叉验证结果。但上述过程,为大家展现了如何选择正确的核函数,以及如何调整核函数的参数,过程虽然简单,但是希望可以对大家有所启发。








 本文探讨了SVM在处理软间隔数据时的推广,解释了硬间隔与软间隔的区别,并重点介绍了重要参数C的含义。C参数用于权衡训练样本的正确分类与决策函数的边际最大化,影响模型复杂度和训练准确性。较高的C值倾向于提高训练精度,而较低的C值则追求更大边际。通过调整C,可以找到适合数据集的最优模型。
本文探讨了SVM在处理软间隔数据时的推广,解释了硬间隔与软间隔的区别,并重点介绍了重要参数C的含义。C参数用于权衡训练样本的正确分类与决策函数的边际最大化,影响模型复杂度和训练准确性。较高的C值倾向于提高训练精度,而较低的C值则追求更大边际。通过调整C,可以找到适合数据集的最优模型。
















 2784
2784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








