线性回归：多重共线性的相关数学推导

最新推荐文章于 2025-10-11 00:14:12 发布

原创

最新推荐文章于 2025-10-11 00:14:12 发布 · 2.5k 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #机器学习 #统计 #多重共线性 #相关性

本文深入探讨了线性回归中多重共线性的问题，指出逆矩阵存在的必要条件是矩阵行列式不为0，即特征矩阵不能存在多重共线性。介绍了满秩矩阵的概念，并讨论了相关性和多重共线性的区别。提出了处理多重共线性的三种常见方法：数据预处理、向前逐步回归和改进线性回归算法，如岭回归、Lasso和弹性网。

多元线性回归使用最小二乘法求解，对多元线性回归的损失函数求导，并得出求解系数的式子和过程：
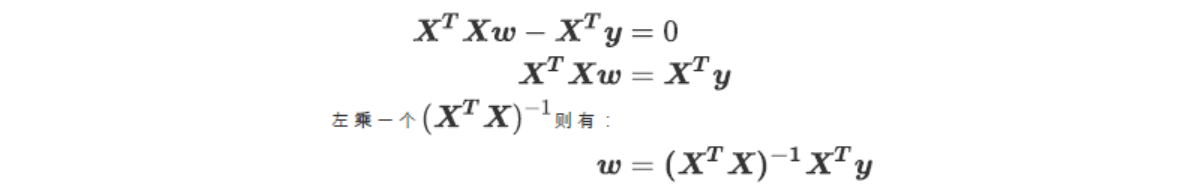
在这里插入图片描述
最后一步中需要左乘X^TX的逆矩阵，而逆矩阵存在的充分必要条件是特征矩阵不存在多重共线性。什么是多重共线性，如何一步步从逆矩阵必须
存在推导到多重共线性不能存在?

逆矩阵存在的充要条件

逆矩阵存在与否的意义和影响。一个矩阵什么情况下才可以有逆矩阵呢？来看逆矩阵的计算公式：
$A−1=1∣A∣A^{-1}=\Large\frac1{|A|}$ $A^*$
分子上A^*是伴随矩阵，任何矩阵都可以有伴随矩阵，因此这一部分不影响逆矩阵的存在性。而分母上的行列式|A|就不同了，位于分母的变量不能为0，一旦为0则无法计算出逆矩阵。因此逆矩阵存在的充分必要条件是：矩阵的行列式不能为0，对于线性回归而言，即是说|X^TX|不能为0。这是使用最小二乘法来求解线性回归的核心条件之一。

行列式不为0的充要条件

那行列式要不为0，需要满足什么条件呢？假设特征矩阵X结构为(m,n)，则X^TX就是结构为(n,m)的矩阵乘以结构为(m,n)的矩阵，从而得到结果为
(n,n)的方阵。
$X^TX=(n,m)*(m,n)=(n,n)$
因此，以下所有例子都将以方阵进行举例，方便理解。首先区别一下矩阵和行列式：
$矩阵A=[x11x12x13x21x22x23x31x32x33]矩阵A=\left[ \begin{array}{c}x_{11} & x_{12} & x_{13} \\x_{21} & x_{22} & x_{23} \\x_{31} & x_{32} & x_{33} \\\end{array} \right]$
$矩阵A的行列式=∣x11x12x13x21x22x23x31x32x33∣=∣A∣矩阵A的行列式=\left| \begin{array}{c}x_{11} & x_{12} & x_{13} \\x_{21} & x_{22} & x_{23} \\x_{31} & x_{32} & x_{33} \\\end{array} \right|=|A|$