排序算法：选择排序，基数排序（桶排序）

1.选择排序

选择排序又成为简单选择排序：

以一个整形数组为例：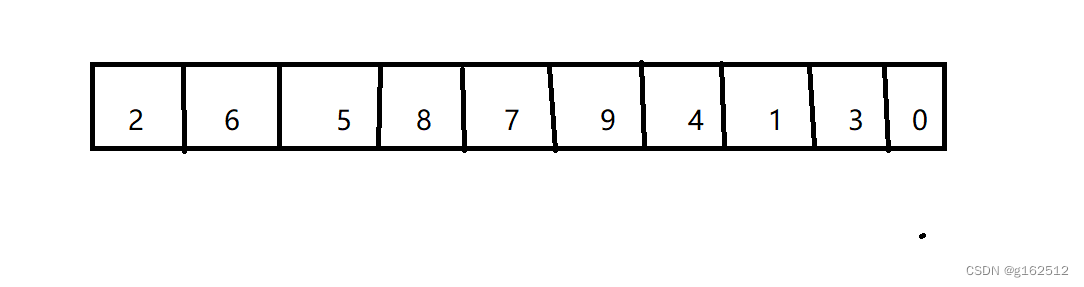

 简单选择排序的思想很简单，就是从待排序队列中找到一个最小值（或者最大值，具体看需求，由小到大排列还是由大到小排列），然后与第一个元素交换，再从后面找到一个最小值，和第二个元素交换，一直到数组元素全部有序。（也就是交换n-1次）n为数组长度。

 

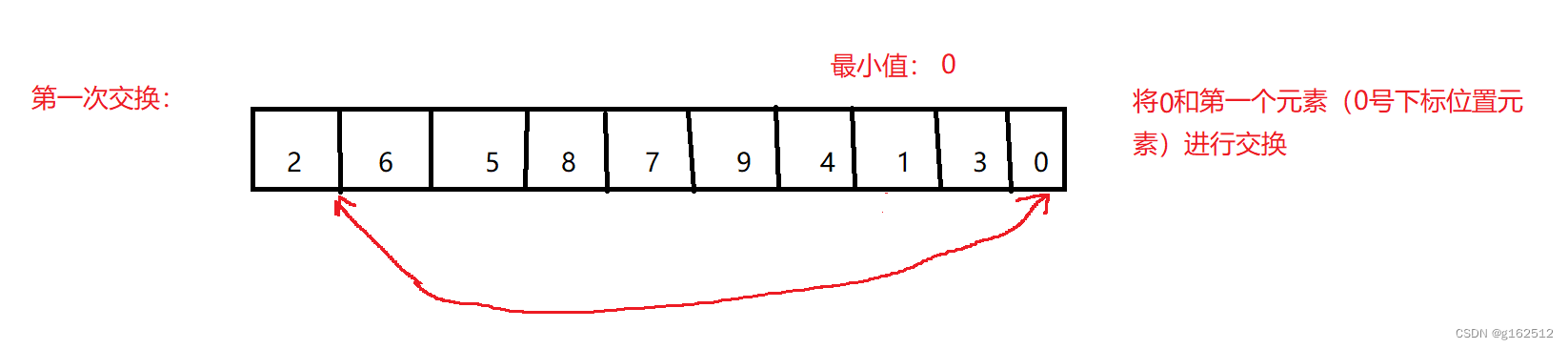
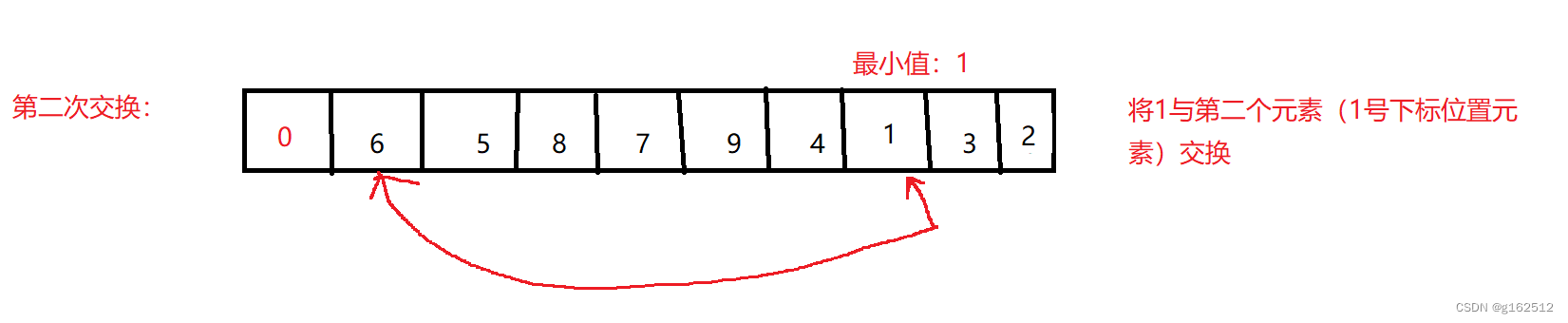
 以此类推，一直到数组完全有序

显然，他的时间复杂度是O(n^2)，空间复杂度为O(1)；

并且它存在跳跃交换，因此是一个不稳定的算法。

代码：

int arr[] = { 2,6,5,8,7,9,4,1,3,0};
	int len = sizeof(arr) / sizeof(arr[0]);

	for (int i = 0; i < len-1; ++i)
	{	
		int min = i;
		for (int j = i+1; j < len; ++j)
		{
			
			if (arr[min] > arr[j])
			{
				min = j;
			}
		}
		int tmp = arr[min];
		arr[min] = arr[i];
		arr[i] = tmp;
	}

2.基数排序（桶排序）

基数排序，也成为桶排序：

其思想是将整数按位数切割成不同的数字，然后按每个位数分别比较。一直从个位到十位到百位等等一直到最高位数的最高位。

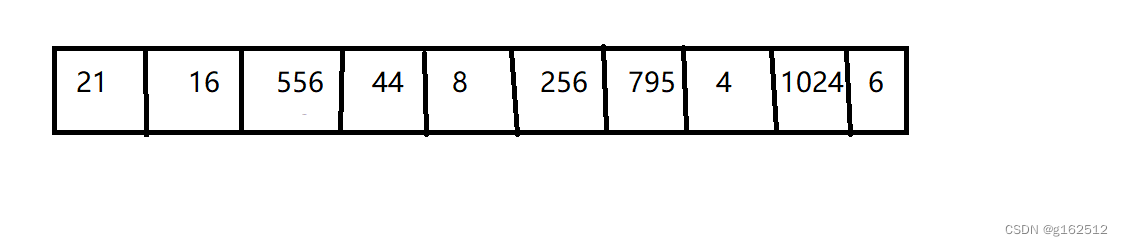
 桶排序思想比较简单：

第一次排序，将所有个位数为0的数放在0号桶中（可以把桶想象为一个队列，或者直接把桶设置为队列），个位数为1的放入1号桶，个位数为2的放入2号桶等等等等，一直放完数据；

然后将所有桶中的数据按照先进先出的原则（和队列相似），从0号桶开始一直到9号桶，将数组取出来，再按照十位数进行入桶：十位为0的放入0号桶中，十位为1的放入1号桶中以此类推，再将数组取出来按照百位数进行排放，一直到最高位数的最高位放完取完，排序也就完成了。

 

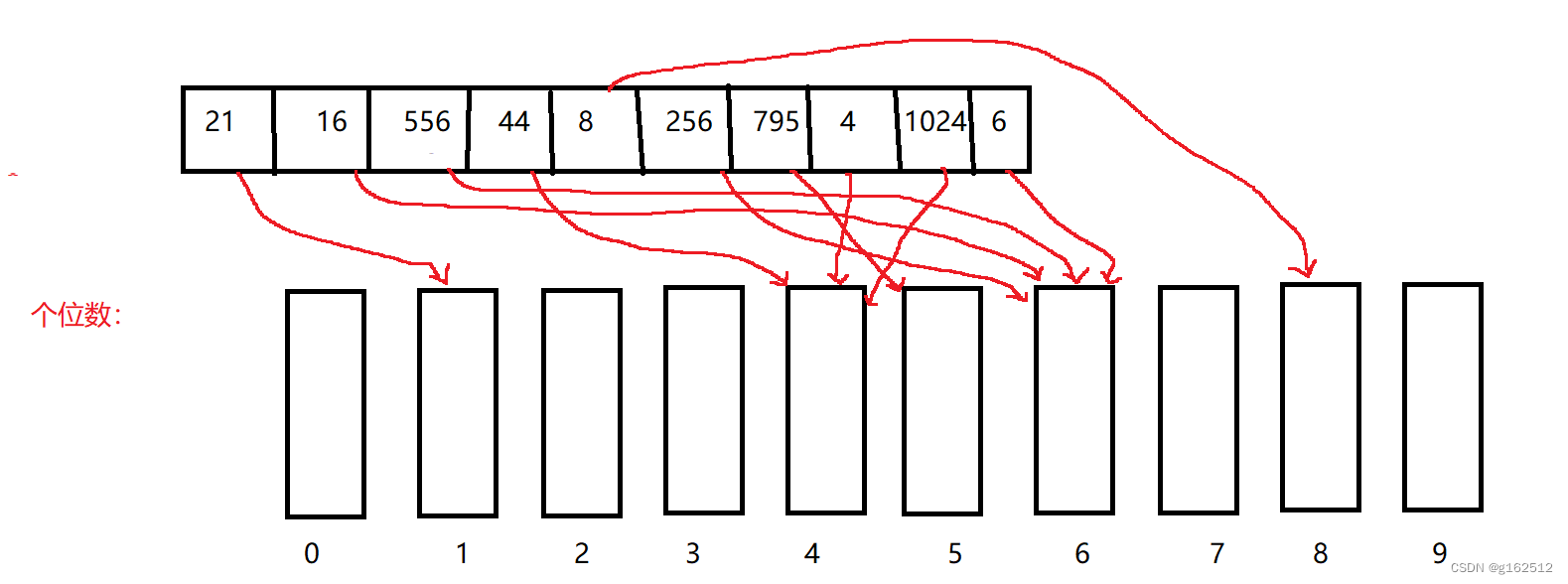
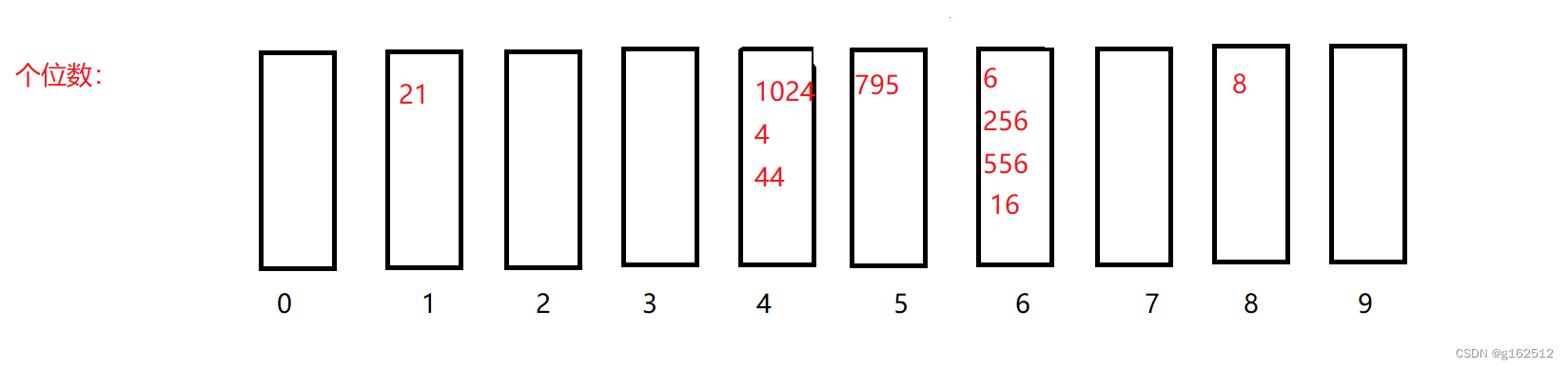
 再全部取出来就是：

21   44  4  1024  795  16  556  256  6  8

再接着基于个位数的结果继续十位数入桶：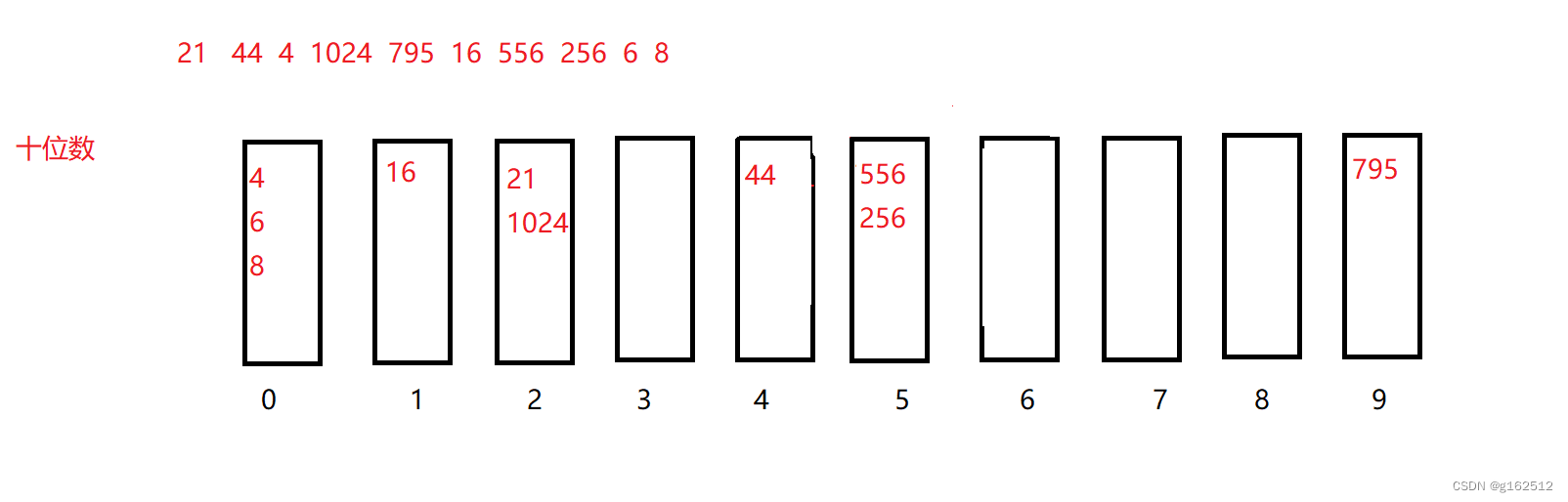

 全部取出来：

4  6  8  16  21  1024  44  556  256  795

再次以十位的结果进行百位入桶：

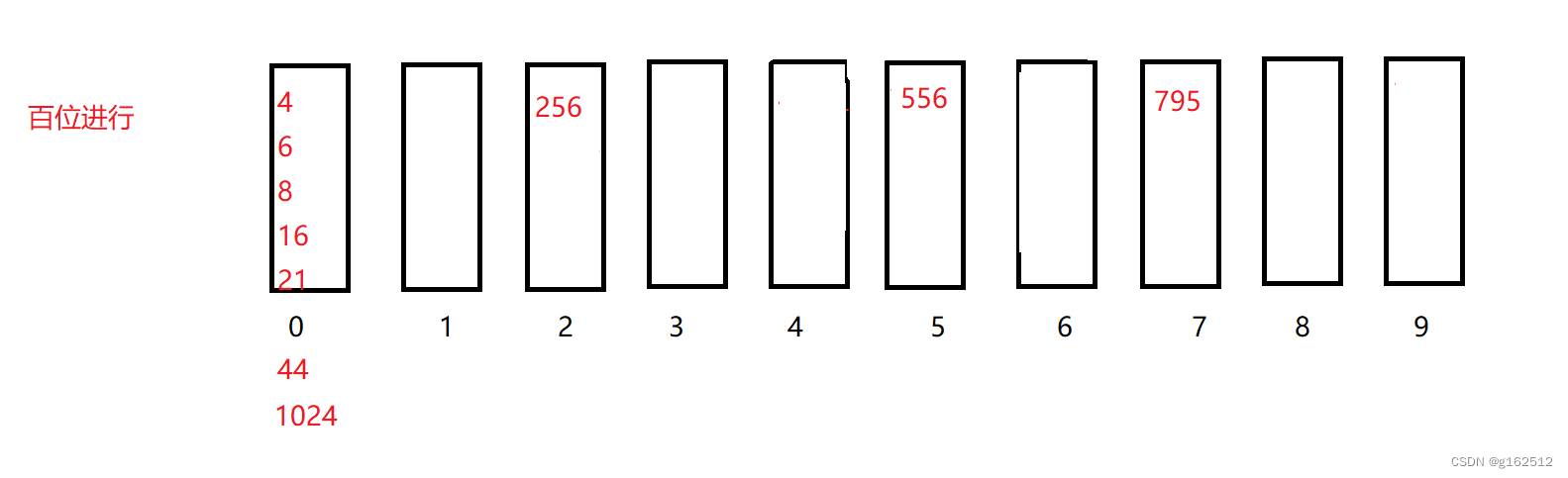
 全部取出：

4  6  8  16  21  44  1024  256  556  795

再进行一次千位入桶即可。

桶排序的时间复杂度比较特殊，它的时间复杂度基于最大数据的位数，假设最大位数有d位，那么基数排序的时间复杂度位O(dn)，他的空间复杂度也被最大位数d影响，其空间复杂度位O(d+n)，并且由于没有跳跃交换，他是一个特别稳定的算法！

基数排序代码：（模拟队列来实现桶）

typedef struct MyQueue
{
	int data;
	MyQueue* next;
}qu;

void Initqu(qu& q)
{
	q.next = nullptr;
}
void Pushqu(qu& q, int val)
{
	qu* p = new qu{};
	p->data = val;
	p->next = q.next;
	q.next = p;
}
int Popqu(qu& q)
{
	qu* p = &q;
	int n = 0;
	if (p->next != nullptr)
	{
		for (p; p->next->next != nullptr; p = p->next);
		qu* dq = p->next;
		n = dq->data;
		p->next = nullptr;
		delete dq;
		dq = nullptr;
	}
	return n;
}


void Sort_Card(int* arr,int len,int fin)
{
	int n = 0;
	int num[10] = { 0 };
	qu Card[10] = {};
	while (n<len)
	{
		int index = arr[n];
		for (int i = 0; i < fin; ++i)
		{
			index = index/10;
		}
		index =index%10;
		Pushqu(Card[index], arr[n]);
		++num[index];
		++n;
	}
	n = 0;
	

	for (int i = 0; i < 10; ++i)
	{
		for (int j = 0; j < num[i]; ++j)
		{
			arr[n++] = Popqu(Card[i]);
		}
		num[i] = 0;
	}
}



int main()
{
	int arr[] = { 15,44,889,62,336,14,5,6,2,449,5542,776,34,6418,128 };
	int count = 0;
	int len = sizeof(arr) / sizeof(arr[0]);
	int Maxarr = arr[0];
	for (int i = 1; i < len; ++i)
	{
		if (arr[i] > Maxarr)
		{
			Maxarr = arr[i];
		}
	}
	while (Maxarr)
	{
		++count;
		Maxarr /= 10;
	}
	for (int i = 0; i < count; ++i)
	{
		Sort_Card(arr, len, i);
	}
	for (int i = 0; i < len; ++i)
	{
		cout << arr[i] << "   ";
	}
}

感谢阅读！