js 浮点数计算精度丢失问题

最新推荐文章于 2025-05-15 13:59:00 发布

原创最新推荐文章于 2025-05-15 13:59:00 发布 · 1.6k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#js #浮点数 #精度丢失

项目开发经验专栏收录该内容

19 篇文章

订阅专栏

本文探讨了JavaScript中浮点数计算存在的精度丢失问题，并提供了两种解决方案：一是通过升幂和降幂转换来规避精度问题；二是利用toFixed函数对结果进行格式化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

js 浮点数计算精度丢失问题

在使用js函数进行小数计算时，发现计算存在精度丢失的问题。
例如：4.35*100
其他工具计算结果为 435
但使用js计算的结果却不是，浏览器截图为证

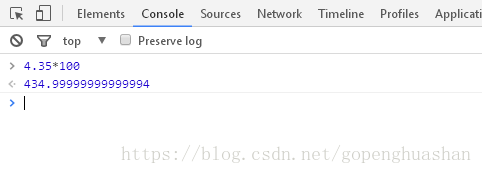
这里写图片描述

成因：对于浮点数计算，所有的语言都有误差，只是对于c、c++、java等高级语言，已经封装处理过了，而对于js这种弱语言，设计之初就没考虑对浮点数进行严格的控制，所以有该问题。当4.35 用二进制表示为100.0101100110011001….无限循环，自然有精度丢失。

如何解决：
1 （推荐方法）通过升幂，将小数转为计算机能精准识别的整数，计算完再降幂。eg: (0.1*10+0.2*10)/10=0.3
2 （一般方法）使用tofixed函数，对于金额数要求高的场景不建议。eg:

<html>
<head>
<script type="text/javascript">
function displaynum()
{
var num = new Number(4.35*100);
alert(num.toFixed(2));
}
</script>
</head>
<body>

Show the number 4.35*100 with one decimal:

<form>
<input type="button" value="Show!" onclick="displaynum()" >
</form>

</body>
</html>