深度神经网络原理

深度神经网络原理

感谢前辈们百忙中抽空做的ppt

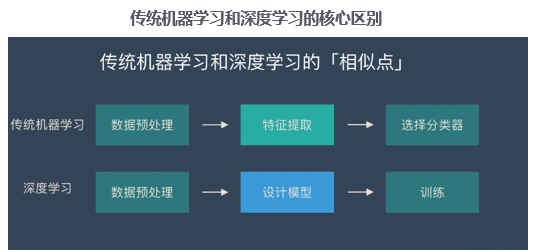
1. 深度神经网络介绍

简单地说，深度学习就是把计算机要学习的东西看成一大堆数据，把这些数据丢进一个复杂的、包含多个层级的数据处理网络（深度神经网络），然后检查经过这个网络处理得到的结果数据是不是符合要求——如果符合，就保留这个网络作为目标模型，如果不符合，就一次次地、锲而不舍地调整网络的参数设置，直到输出满足要求为止。

2. DNN的基本结构

基本神经网络的相互连接的人工神经元分为三层：

**输入层：**来自外部世界的信息通过输入层进入人工神经网络。输入节点对数据进行处理、分析或分类，然后将其继续传递到下一层。

**隐藏层：**隐藏层从输入层或其他隐藏层获取其输入。人工神经网络可以具有大量的隐藏层。每个隐藏层都会对来自上一层的输出进行分析和进一步处理，然后将其继续传递到下一层。

**输出层：**输出层提供人工神经网络对所有数据进行处理的最终结果。它可以包含单个或多个节点。例如，如果我们要解决一个二元（是/否）分类问题，则输出层包含一个输出节点，它将提供 1 或 0 的结果。但是，如果我们要解决一个多类分类问题，则输出层可能会由一个以上输出节点组成。

DNN（深度神经网络）按不同层的位置划分内部的神经网络层可以分为三类，输入层，隐藏层和输出层。如下图示例，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。

其中，层与层之间是全连接的，也就是说，第 i 层的任意一个神经元一定与第 i+1 层的任意一个神经元相连。

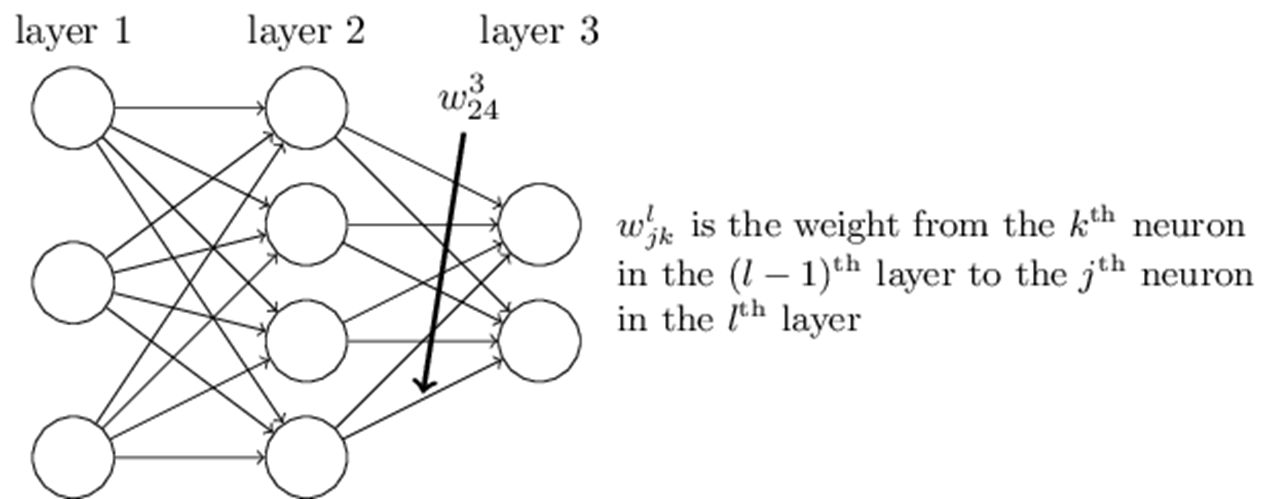
首先我们来看看线性关系系数 w 的定义。以下图一个三层的 DNN 为例，第二层的第 4 个神经元到第三层的第 2 个神经元 的线性系数定义为$w_{2,4}^3$,上标3代表线性系数w所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。

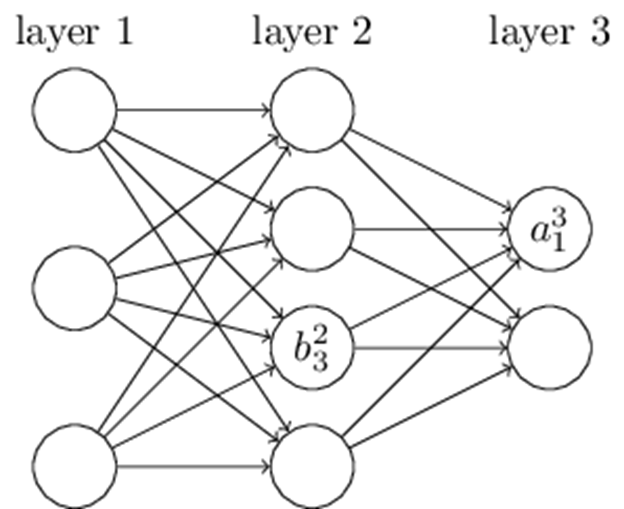
再来看看偏倚 b 的定义。以三层的DNN为例，第二层的第三个神经元对应的偏倚定义为 。其中，上标 2 代表所在的层数，下标 3 代表偏倚所在的神经元的索引。

偏置本质上是一个常数项，是神经元独立于输入所拥有的一点“自由度”。在每次输出计算中，神经元会先把所有输入乘以对应权重，加权求和之后，再加上这个偏置值。

3. DNN的前向传播

所谓的 DNN（深度神经网络） 的 前向传播算法 也就是利用我们的若干个 权重系数矩阵 W ，偏倚向量 b 来和输入值向量 x 进行一系列 线性运算 和 激活运算 ，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。

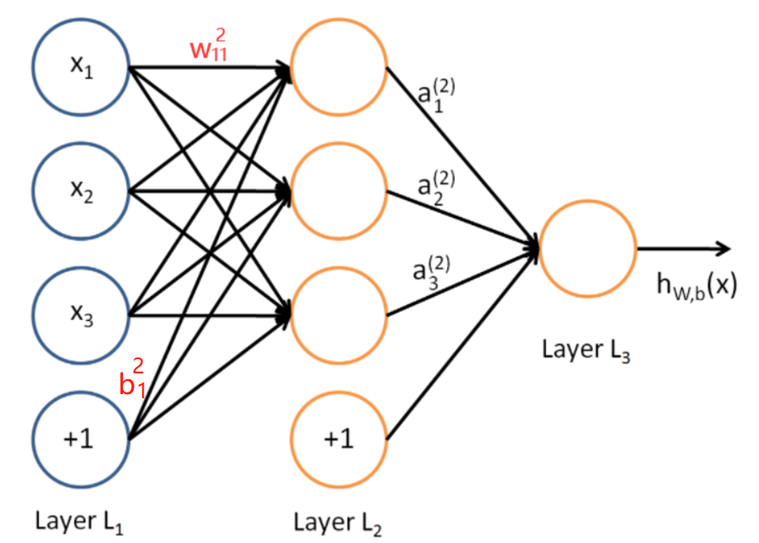
假设我们选择的激活函数是 σ(z)，隐藏层和输出层的输出值为 a，则对于下图的三层 DNN ,利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，则有：

将上例的式子一般化，假设第 i 层共有 m 个神经元，则对于第 i 层的第 j 个神经元的输出，我们有：

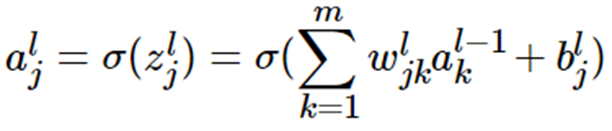
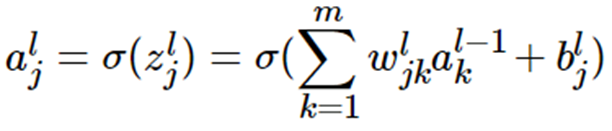
如果将其转化为矩阵表示：

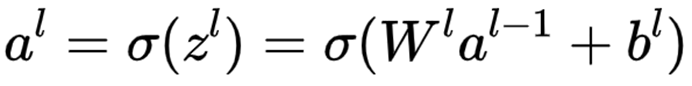
可以看到，神经网络的结构一般是先进行升维（神经元个数增多），再进行降维（神经元个数减少）的操作。

比如我们在图中看到的这一组运算，就是一个非常典型的线性变换过程：

输入是 2 个特征的数据，通过一个形状为 m 的隐藏层神经元矩阵加上偏置，得到一个新的向量。这个新的向量维度比输入更高，所以可以理解为完成了“升维”。

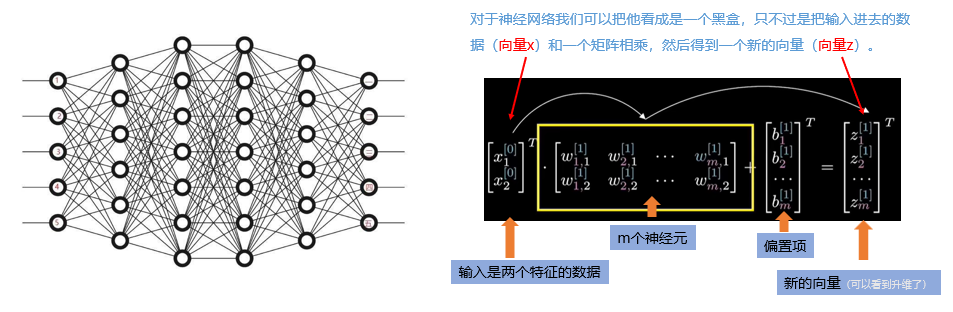
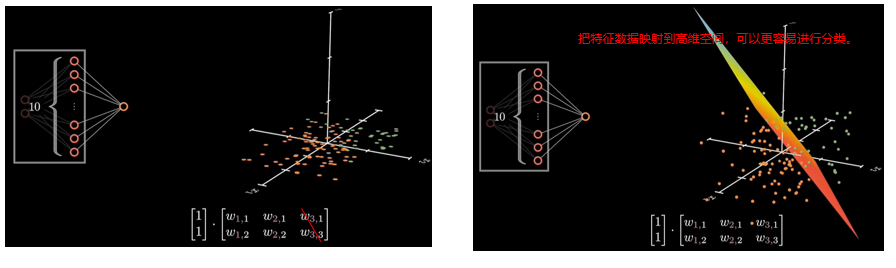
把特征从低维空间映射到高维空间的意义在于，可以让模型更容易完成分类。

我们来看图中左边这个神经网络：如果现在我们把数据投影到一个二维的平面，如果我们要对绿色的小点和橙色的小点做一个分割，其实是很难的，或者说我们要构造一个非常复杂的函数才可以进行分类，

但是如果我们把数据投影到一个更加高维的空间，那么我们就可以通过一个超平面对其进行分割你会发现，一旦我们把原始数据投影到了更高的空间，很多原本在二维空间中难以分开的数据，在高维空间里就变得容易区分了。

所以，从直觉上说，神经网络的前向传播做的事，其实就是不断把数据“拉直”“展开”，让模型能更容易地找到分界线，实现分类或回归的任务。

前面的神经元层会提取出越来越抽象的特征，比如边缘、笔画方向；

而在接近输出层时，我们不再需要那么多冗余的信息，只需要那些能决定分类的高层语义特征。

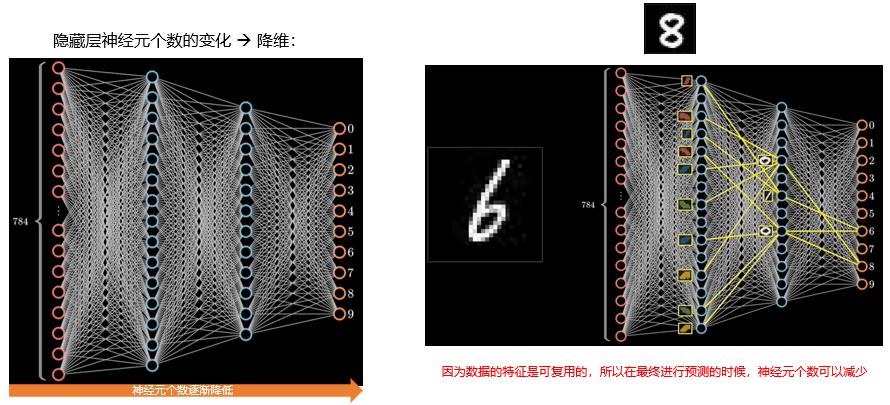
所以，网络结构设计上，往往采用“宽进窄出”的方式，先升维提取丰富特征，再降维压缩信息用于最终分类。

右图展示的是当我们输入一张“6”或者“8”的图像时，前面层提取的是一些局部结构特征，比如弯曲、闭合或者拐角等；

而这些特征在后面的层会被进一步组合成更复杂的表示，最终在输出层转化为对数字的概率预测。

在预测阶段，特征是可复用的，所以最终阶段的神经元数量可以适当减少，从而提升模型效率。

接下来我们看一下激活函数的作用。

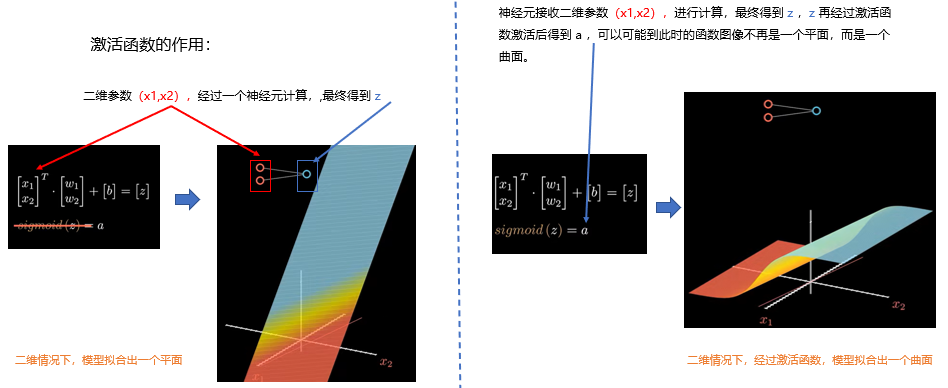
假设我们有一个二维输入向量 (x1,x2)，它经过一个神经元的计算，首先会进行一次仿射变换，也就是将输入向量与权重向量做点积，加上偏置项，得到一个标量 z。

在几何空间中，这个过程可以理解为：我们在二维空间中拟合出一个平面，这个平面是输入空间到神经元空间的线性映射。

但仅有线性变换是不够的。右边这张图展示了我们引入激活函数之后的情况，比如 $\sigma$ 函数。

激活函数的作用是引入非线性，它把线性输出 z映射成另一个值 a，让模型能够学习更复杂、更灵活的函数形式。

从几何上看，原本是一个平面，现在变成了一个具有曲率的曲面。这种非线性的引入，是深度学习区别于传统线性模型的关键。

4. DNN反向传播(BP算法)

BP算法是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

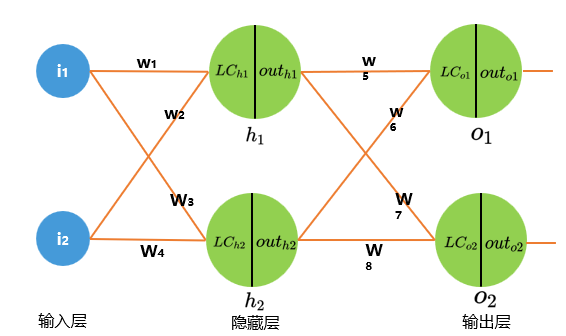
现有三层神经网络，场景如下所示：

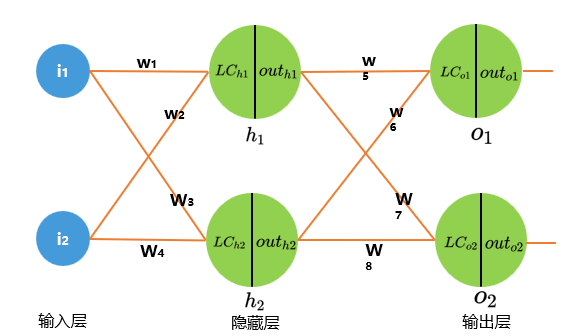
LC（Linear combination）意为线性组合，$L{C}_{h1}$ 表示隐藏层 h1 的输入值，也就是 $i_1$ 输入层经过线性组合的输出值。

$ou{t}_{h1}$ 表示隐藏层 h1 经过激活函数转换后的输出值。

1）定义损失函数，采用 均方损失 为例：

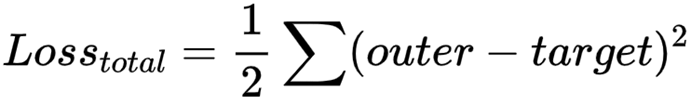
上述三层神经网络损失表达式：

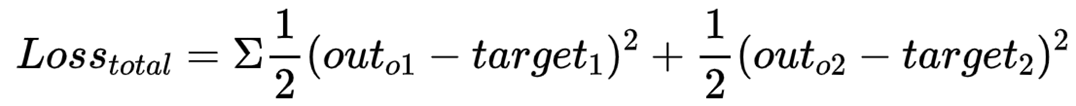
2）定义激活函数：采用 Sigmoid 激活函数：

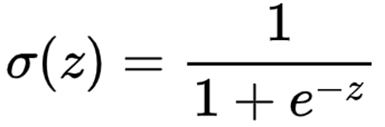
3）更新参数的方法，随机梯度下降法：开始先随机生成一个 w ，然后用下面的公式不断更新 w 的值，最终能够逼近真实结果。

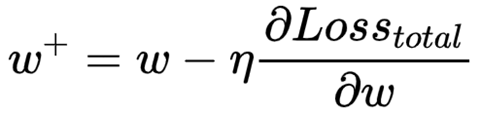
以第一次更新参数 w5 和 b5为例：

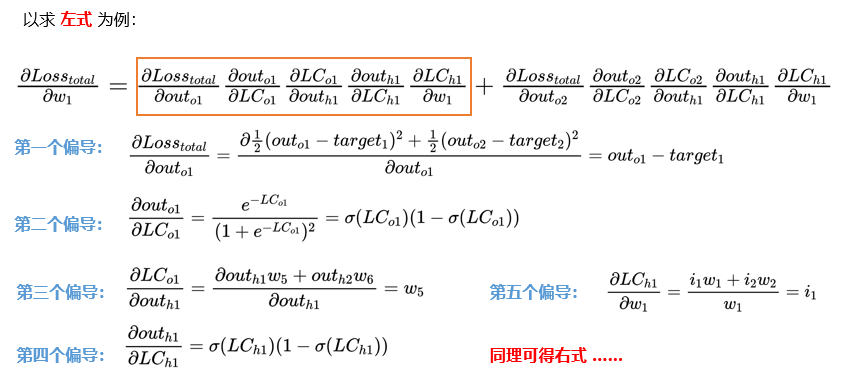
1）求解损失函数对 w5 的偏导数：

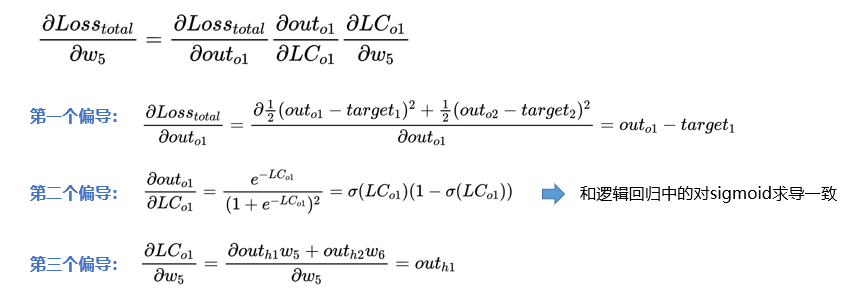
则，对 w5 求 偏导数的总公式 为：

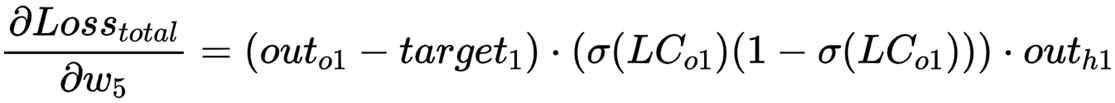
按照同样的方法，我们可以得到 b5 的偏导：

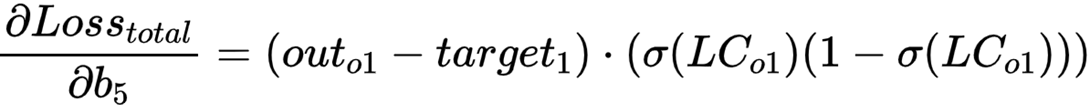
更新参数 w5 和 b5 。

第一次更新时，我们需要给参数w赋予一个初始值

接下来更新参数 w1 ，需要注意的是此时参数 w1 不仅受到 O1 的影响还受到 O2 的影响。

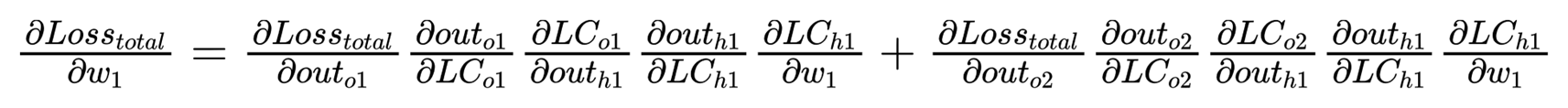
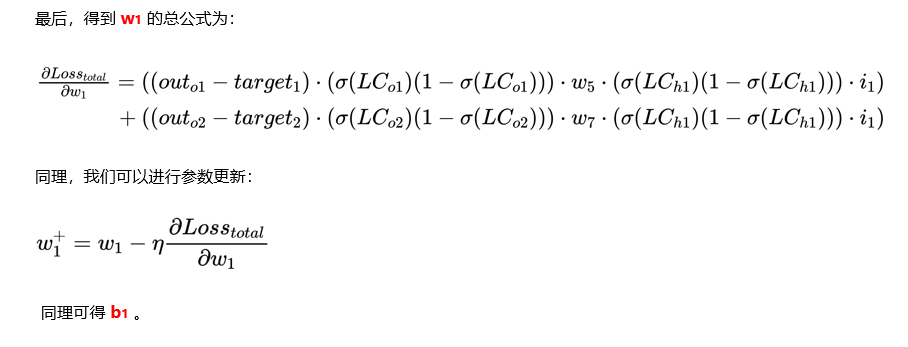
5. DNN正则化

在前面的损失函数中，我们仅考虑了模型预测与真实标签之间的误差。然而，这样的设计容易让模型在训练集上过拟合，失去对新样本的泛化能力。

为了解决这一问题，我们引入了正则化项，对模型的复杂度进行约束。

1. L1,L2正则化

我们可以看到，原始的损失函数是基于预测结果与真实值之间的平方误差。而在引入 L2 正则化之后，我们在原有损失的基础上，额外加入了一项权重平方和的惩罚项，用以抑制过大的参数，从而提升模型的鲁棒性。

L2 正则化也被称为权重衰减，它鼓励参数接近于零但不完全为零，从而保留更多的特征表达能力。

当然，除了 L2，我们也可以采用 L1 正则化，它使用权重的绝对值求和作为惩罚项，更具稀疏性，常用于特征选择。

简而言之，正则化让我们的模型更小、更稳、更抗干扰，是深度学习模型能够落地的重要保障。

当我们的每个样本的损失函数是均方差损失函数,则所有的 m 个样本的损失函数为：

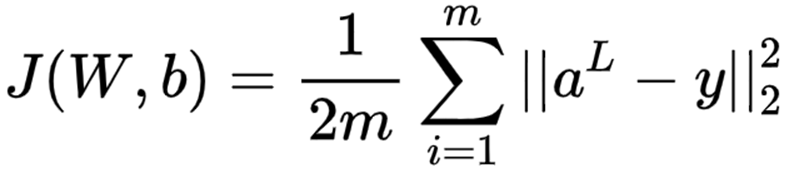
则加上了 L2 正则化后的损失函数是

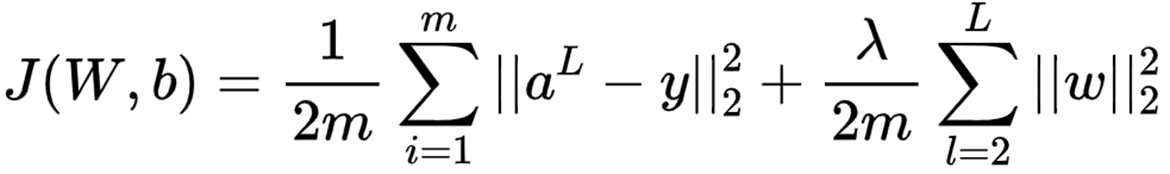
2. Dropout层

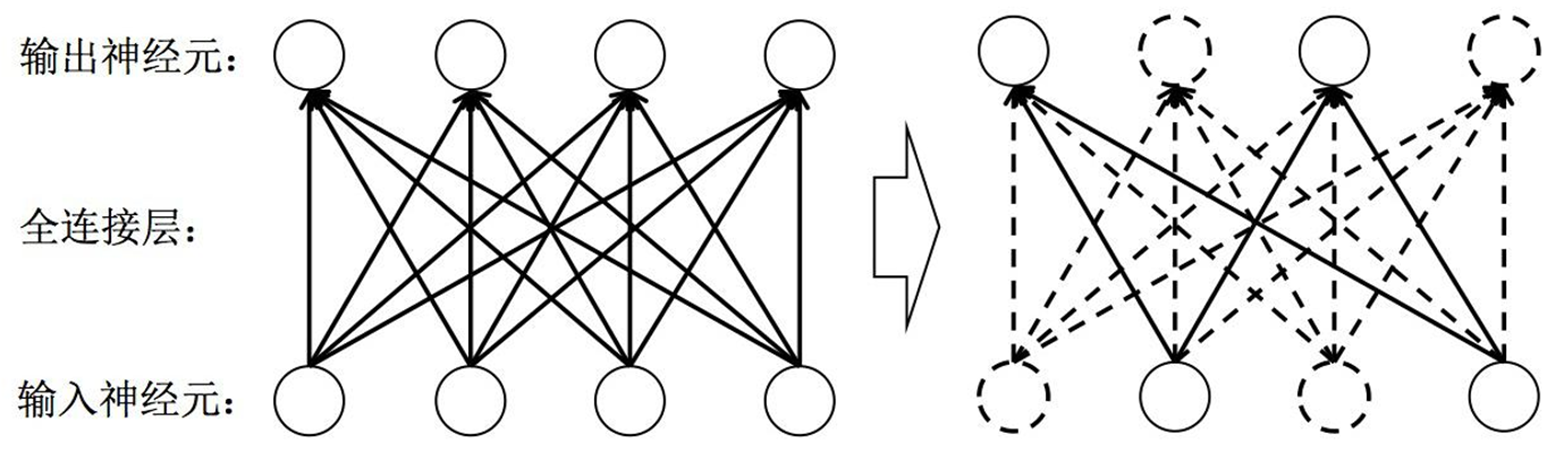
Dropout 是常用的一种正则化方法，Dropout层是一种正则化层。全连接层参数量非常庞大（占据了神经网络模型参数量的80%～90%左右），发生过拟合问题的风险比较高，所以我们通常需要一些正则化方法训练带有全连接层的神经网络模型。在每次迭代训练时，将神经元以一定的概率值暂时随机丢弃，即在当前迭代中不参与训练。

通过这种方式，模型被迫不能依赖某几个特定神经元的“惯性表达”，而是要学会在多个不同的子结构上进行信息融合。这样训练出来的模型更有泛化能力，更健壮。

值得注意的是：Dropout只在训练阶段启用，到了测试阶段，我们会使用完整的网络结构，并将神经元的输出按比例缩放，以弥补训练时的缺失。因此，Dropout 并不是减少模型的容量，而是通过“随机性”提升模型的鲁棒性，是一种非常经典且有效的正则化手段。

参考

ppt

机器学习：基本概念，损失函数，特征工程 燕双嘤