该博客记录了LeetCode多道题目的解答。涉及反转字符串、01矩阵、二叉树直径等题目，运用了模拟、广度优先搜索、动态规划、递归等算法，还使用了前缀和、哈希表等数据结构技巧，对各题给出分析思路与提交结果。
文章目录
前言
需要开通vip的题目暂时跳过
笔记导航
点击链接可跳转到所有刷题笔记的导航链接
541. 反转字符串 II
给定一个字符串 s 和一个整数 k，你需要对从字符串开头算起的每隔 2k 个字符的前 k 个字符进行反转。
如果剩余字符少于 k 个，则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。
-
解答
public String reverseStr(String s, int k) { char[] chars = s.toCharArray(); for(int i =0;i < s.length();i += 2*k){ int start = i; int end = i + 2 * k - 1; if(end < s.length()){ reverse(chars,start,end - k); }else{ end = s.length()-1; if(end - start < k){ reverse(chars,start,end); }else{ end = start + k - 1; reverse(chars,start,end); } } } return new String(chars); } public void reverse(char[] chars,int start,int end){ for(int i = 0;i <= (end - start)/2;i++){ char temp = chars[start + i]; chars[start + i] = chars[end - i]; chars[end - i] = temp; } } -
分析
- 模拟题意
- 一次遍历寻找反转字符串的起始位置和结束位置，然后进行反转
-
提交结果
542. 01 矩阵
给定一个由 0 和 1 组成的矩阵，找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
-
解答
//方法1 广度优先搜索 public int[][] updateMatrix(int[][] matrix) { if (matrix == null || matrix.length == 0) return null; int m = matrix.length, n = matrix[0].length; int[][] res = new int[m][n];//结果集 boolean[][] visited = new boolean[m][n];//记录已经计算过的位置 Queue<int[]> queue = new LinkedList<>();//广搜队列 //遍历，将等于0的位置计入结果集并入队 for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (matrix[i][j] == 0) { res[i][j] = 0; visited[i][j] = true; queue.offer(new int[]{i, j}); } } } int[][] direction = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//上下左右 while (!queue.isEmpty()) { int[] poll = queue.poll(); int i = poll[0], j = poll[1]; for (int k = 0; k < 4; k++) { int di = i + direction[k][0], dj = j + direction[k][1]; if (di >= 0 && di < m && dj >= 0 && dj < n && !visited[di][dj]) { res[di][dj] = res[i][j] + 1; visited[di][dj] = true; queue.offer(new int[]{di, dj}); } } } return res; } // 方法2 DP public int[][] updateMatrix(int[][] matrix) { int m = matrix.length, n = matrix[0].length; // 初始化动态规划的数组，所有的距离值都设置为一个很大的数 int[][] dist = new int[m][n]; for (int i = 0; i < m; ++i) { Arrays.fill(dist[i], Integer.MAX_VALUE / 2); } // 如果 (i, j) 的元素为 0，那么距离为 0 for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (matrix[i][j] == 0) { dist[i][j] = 0; } } } // 只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序 for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (i - 1 >= 0) { dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1); } if (j - 1 >= 0) { dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1); } } } // 只有 水平向左移动 和 竖直向下移动，注意动态规划的计算顺序 for (int i = m - 1; i >= 0; --i) { for (int j = 0; j < n; ++j) { if (i + 1 < m) { dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1); } if (j - 1 >= 0) { dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1); } } } // 只有 水平向右移动 和 竖直向上移动，注意动态规划的计算顺序 for (int i = 0; i < m; ++i) { for (int j = n - 1; j >= 0; --j) { if (i - 1 >= 0) { dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1); } if (j + 1 < n) { dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1); } } } // 只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序 for (int i = m - 1; i >= 0; --i) { for (int j = n - 1; j >= 0; --j) { if (i + 1 < m) { dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1); } if (j + 1 < n) { dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1); } } } return dist; } -
分析
-
方法1 广度优先搜索
-
第一次遍历将元素为0的点的坐标入队，并标记为已经访问过。
-
之后就是广度搜索
-
元素出队，往4个方向去走，更新4个方向上到元素0的距离为res[di] [dj] = res[i] [j] + 1，并标记为访问过。
-
新的点入队。
-
直到队空为止
-
方法2 动态规划
-
对于矩阵中的任意一个 1 以及一个 0，我们如何从这个 1 到达 0 并且距离最短呢？根据上面的做法，我们可以从 1 开始，先在水平方向移动，只要与 0 在同一列。随后再在竖直方向上移动，直到到达 0 的位置。这样以来，从一个固定的 1 走到任意一个 0，在距离最短的前提下可能有四种方法：
- 只有 水平向左移动 和 竖直向上移动；
- 只有 水平向左移动 和 竖直向下移动；
- 只有 水平向右移动 和 竖直向上移动；
- 只有 水平向右移动 和 竖直向下移动。
这样以来，我们就可以使用动态规划解决这个问题了。我们用 f(i, j)f(i,j) 表示位置 (i, j)(i,j) 到最近的 0 的距离。如果我们只能「水平向左移动」和「竖直向上移动」，那么我们可以向上移动一步，再移动 f(i - 1, j)f(i−1,j) 步到达某一个 0，也可以向左移动一步，再移动 f(i, j - 1)f(i,j−1) 步到达某一个 0。因此我们可以写出如下的状态转移方程：
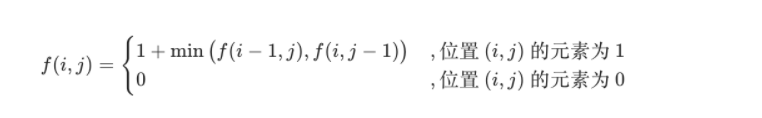
官方题解还提到 可以仅考虑第一种和第四种移动的方法。
-
-
提交结果
方法1
方法2
543. 二叉树的直径
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
-
解答
int max = Integer.MIN_VALUE; public int diameterOfBinaryTree(TreeNode root) { if(root == null)return 0; dfs(root); return max-1; } public int dfs(TreeNode root){ if(root == null)return 0; int left = dfs(root.left); int right = dfs(root.right); max = Math.max(max,1 + left + right); return 1 + Math.max(left,right); } -
分析
- 递归实现
- 判断一个结点左子树的高度和右子树的高度
- 两个子树的高度+1 就是这一条路径上的直径长度。记录下最长的。
-
提交结果
546. 移除盒子
给出一些不同颜色的盒子，盒子的颜色由数字表示，即不同的数字表示不同的颜色。
你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 k*k 个积分。
当你将所有盒子都去掉之后，求你能获得的最大积分和。
-
解答
int[][][] dp = new int[100][100][100]; public int removeBoxes(int[] boxes) { return dfs(boxes,0,boxes.length-1,0); } public int dfs(int[] boxes,int l,int r,int k){ if(l > r) return 0; if(dp[l][r][k] != 0)return dp[l][r][k]; dp[l][r][k] = dfs(boxes,l,r-1,0) + (k + 1) * (k + 1); for(int i = l;i<r;i++){ if(boxes[i] == boxes[r]){ dp[l][r][k] = Math.max(dp[l][r][k],dfs(boxes,l,i,k+1) + dfs(boxes,i+1,r-1,0)); } } return dp[l][r][k]; } -
分析
- 动态规划思想
- dp[l] [r] [k] 表示在区间l - r的范围内，r之后有k个元素和boxes[r]相同的情况下最大积分和。
- 目标就是求dp[0] [boxes.length-1] [0]
- 初始化全部为0.
- 从l遍历到r
- 若出现了i 位置对应的数字等于r位置对应的数字 那么k + 1，而i ～ r 之间的我们就要消灭它，即dfs(boxes, i + 1,r-1,0)
- 所以动态转移方程为
- dp[l] [r] [k] = Math.max(dp[l] [r] [k], dfs(boxes,l,i,k+1) + dfs(boxes,l+1,r-1,0));
- 在递归的过程中，若出现l > r 返回0，dp[l] [r] [k] 记忆集中不为0，直接返回对应的值，避免重复计算。
-
提交结果
547. 朋友圈
班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
-
解答
public int findCircleNum(int[][] M) { int N = M.length; int[] visited = new int[N]; int res = 0; for(int i = 0;i < N;i++){ if(visited[i] == 0){ visited[i]=1; res++; dfs(M,i,visited); } } return res; } public void dfs(int[][] M,int cur,int[] visited){ for(int i = 0;i< M.length;i++){ if(visited[i] == 0 && M[cur][i] == 1 && cur !=i){ visited[i] = 1; dfs(M,i,visited); } } } -
分析
- 图的dfs
-
提交结果
552. 学生出勤记录 II
给定一个正整数 n，返回长度为 n 的所有可被视为可奖励的出勤记录的数量。 答案可能非常大，你只需返回结果mod 109 + 7的值。
学生出勤记录是只包含以下三个字符的字符串：
- ‘A’ : Absent，缺勤
- ‘L’ : Late，迟到
- ‘P’ : Present，到场
如果记录不包含多于一个’A’（缺勤）或超过两个连续的’L’（迟到），则该记录被视为可奖励的。
-
解答
public int checkRecord(int n) { long mod = 1000000007; long[][][] dp = new long[n+1][2][3]; dp[1][0][0] = 1; dp[1][1][0] = 1; dp[1][0][1] = 1; for(int i = 2;i <= n;i++){ //+p dp[i][0][0] = (dp[i-1][0][0] + dp[i-1][0][1] + dp[i-1][0][2]) % mod; dp[i][1][0] = (dp[i-1][1][0] + dp[i-1][1][1] + dp[i-1][1][2]) % mod; //+L dp[i][0][1] = dp[i-1][0][0]; dp[i][0][2] = dp[i-1][0][1]; dp[i][1][1] = dp[i-1][1][0]; dp[i][1][2] = dp[i-1][1][1]; //+A dp[i][1][0] += (dp[i-1][0][0] + dp[i-1][0][1] + dp[i-1][0][2]) % mod; } return (int)((dp[n][0][0] + dp[n][1][0] + dp[n][0][1] + dp[n][0][2] + dp[n][1][1] + dp[n][1][2]) % mod); } -
分析
-
对于字母A，我们只在乎它有没有出现过，即出现1次或0次，若出现过了 则不能再出现。
-
对于字母L，我们只在乎它有没有连续的出现，记连续出现的次数
-
可以在已有字母的基础上追加字母ALP，这样仅需要考虑最后的两个字母是否是连续的L即可。
-
所以可以用dp[n] [i] [j]表示n个字母的时候，出现了i个A和末位有j个L的字符串的数量。
-
一共有6种状态
- dp[n] [0] [0] 表示没有A，末位两位没有L 情况下字符串的数量
- dp[n] [0] [1] 表示没有A，最后一位是L 情况下字符串的数量
- dp[n] [0] [2] 表示没有A，最后两位都是L 情况下字符串的数量
- dp[n] [1] [0] 表示有A，末位两位没有L 情况下字符串的数量
- dp[n] [1] [1] 表示有A，最后一位是L 情况下字符串的数量
- dp[n] [1] [2] 表示有A，最后两位都是L 情况下字符串的数量
-
初始条件
- dp[1] [0] [0] = 1 字符串由字母P构成
- dp[1] [1] [0] = 1 字符串由字母A构成
- dp[1] [0] [1] = 1 字符串由字母L构成
-
从2开始追加字母
-
追加字母P的动态转移方程为
dp[i] [0] [0] = (dp[i-1] [0] [0] + dp[i-1] [0] [1] + dp[i-1] [0] [2]) % mod;
dp[i] [1] [0] = (dp[i-1] [1] [0] + dp[i-1] [1] [1] + dp[i-1] [1] [2]) % mod;
-
追加字母L的动态转移方程为
dp[i] [0] [1] = dp[i-1] [0] [0];
dp[i] [0] [2] = dp[i-1] [0] [1];
dp[i] [1] [1] = dp[i-1] [1] [0];
dp[i] [1] [2] = dp[i-1] [1] [1];
-
追加字母A的动态转移方程为
dp[i] [1] [0] += (dp[i-1] [0] [0] + dp[i-1] [0] [1] + dp[i-1] [0] [2]) % mod;
注意这里是+= 因为在追加字母P的时候已经计算过dp[i] [1] [0]了，所以需要加上。
-
-
-
提交结果
553. 最优除法
给定一组正整数，相邻的整数之间将会进行浮点除法操作。例如， [2,3,4] -> 2 / 3 / 4 。
但是，你可以在任意位置添加任意数目的括号，来改变算数的优先级。你需要找出怎么添加括号，才能得到最大的结果，并且返回相应的字符串格式的表达式。你的表达式不应该含有冗余的括号。
-
解答
//递归 public String optimalDivision(int[] nums) { T t = optimal(nums, 0, nums.length - 1); return t.max_str; } class T { float max_val, min_val; String min_str, max_str; } public T optimal(int[] nums, int start, int end) { T t = new T(); if (start == end) { t.max_val = nums[start]; t.min_val = nums[start]; t.min_str = "" + nums[start]; t.max_str = "" + nums[start]; return t; } t.min_val = Float.MAX_VALUE; t.max_val = Float.MIN_VALUE; t.min_str = t.max_str = ""; for (int i = start; i < end; i++) { T left = optimal(nums, start, i); T right = optimal(nums, i + 1, end); if (t.min_val > left.min_val / right.max_val) { t.min_val = left.min_val / right.max_val; t.min_str = left.min_str + "/" + (i + 1 != end ? "(" : "") + right.max_str + (i + 1 != end ? ")" : ""); } if (t.max_val < left.max_val / right.min_val) { t.max_val = left.max_val / right.min_val; t.max_str = left.max_str + "/" + (i + 1 != end ? "(" : "") + right.min_str + (i + 1 != end ? ")" : ""); } } return t; } //方法2 记忆化递归 public String optimalDivision(int[] nums) { T[][] memo = new T[nums.length][nums.length]; T t = optimal(nums, 0, nums.length - 1,memo); return t.max_str; } class T { float max_val, min_val; String min_str, max_str; } public T optimal(int[] nums, int start, int end,T[][] memo) { if(memo[start][end] != null) return memo[start][end]; T t = new T(); if (start == end) { t.max_val = nums[start]; t.min_val = nums[start]; t.min_str = "" + nums[start]; t.max_str = "" + nums[start]; return t; } t.min_val = Float.MAX_VALUE; t.max_val = Float.MIN_VALUE; t.min_str = t.max_str = ""; for (int i = start; i < end; i++) { T left = optimal(nums, start, i,memo); T right = optimal(nums, i + 1, end,memo); if (t.min_val > left.min_val / right.max_val) { t.min_val = left.min_val / right.max_val; t.min_str = left.min_str + "/" + (i + 1 != end ? "(" : "") + right.max_str + (i + 1 != end ? ")" : ""); } if (t.max_val < left.max_val / right.min_val) { t.max_val = left.max_val / right.min_val; t.max_str = left.max_str + "/" + (i + 1 != end ? "(" : "") + right.min_str + (i + 1 != end ? ")" : ""); } } memo[start][end] = t; return t; } // public String optimalDivision(int[] nums) { if (nums.length == 1) return nums[0] + ""; if (nums.length == 2) return nums[0] + "/" + nums[1]; StringBuilder res = new StringBuilder(nums[0] + "/(" + nums[1]); for (int i = 2; i < nums.length; i++) { res.append("/" + nums[i]); } res.append(")"); return res.toString(); } -
分析
- 要使得数字最大，那么就是要一个大的数字除以一个小的数字。
- 所以考虑分割点，分割点左边得到最大的结果，分割点右边得到最小的结果。
- 递归的过程中，需要记录一个一段数字中可以得到的最大值和最小值以及对应的字符串表达。
- 不需要给左边的表达式加括号仅需要给右边的表达式加括号即可。
- 若右边只存在一个数字，没有运算符号，那么不需要加括号。
- 方法2 加了个记忆集 减少递归的计算量。
- 方法3 因为所有的数都是正整数，所以最大结果的表达式一定是a/(b/c/d/e/…)
-
提交结果
方法1
方法2
方法3
554.砖墙
你的面前有一堵矩形的、由多行砖块组成的砖墙。 这些砖块高度相同但是宽度不同。你现在要画一条自顶向下的、穿过最少砖块的垂线。
砖墙由行的列表表示。 每一行都是一个代表从左至右每块砖的宽度的整数列表。
如果你画的线只是从砖块的边缘经过，就不算穿过这块砖。你需要找出怎样画才能使这条线穿过的砖块数量最少，并且返回穿过的砖块数量。
你不能沿着墙的两个垂直边缘之一画线，这样显然是没有穿过一块砖的。
-
解答
public int leastBricks(List<List<Integer>> wall) { Map<Integer,Integer> map = new HashMap<>(); int max = 0; for(List<Integer> w : wall){ int res = 0; for(int i = 0;i < w.size() - 1;i++){ int num = w.get(i); res += num; int number = map.getOrDefault(res,0); map.put(res,number + 1); max = Math.max(number + 1,max); } } return wall.size() - max; } -
分析
- 利用前缀和，计算出每一行中的差，然后计数放入map当中计数
- 前缀和计数最多的那个值，也就是缝隙最多的地方。
- 最后返回砖墙的高度 减去 这个最大值即可。
-
提交结果
556. 下一个更大元素 III
给定一个32位正整数 n，你需要找到最小的32位整数，其与 n 中存在的位数完全相同，并且其值大于n。如果不存在这样的32位整数，则返回-1。
-
解答
public int nextGreaterElement(int n) { char[] a = ("" + n).toCharArray(); int i = a.length - 2; while (i >= 0 && a[i + 1] <= a[i]) { i--; } if (i < 0) return -1; int j = a.length - 1; while (j >= 0 && a[j] <= a[i]) { j--; } swap(a, i, j); reverse(a, i + 1); try { return Integer.parseInt(new String(a)); } catch (Exception e) { return -1; } } private void reverse(char[] a, int start) { int i = start, j = a.length - 1; while (i < j) { swap(a, i, j); i++; j--; } } private void swap(char[] a, int i, int j) { char temp = a[i]; a[i] = a[j]; a[j] = temp; } -
分析
- 从后往前找第一个小于后一个的数字的位置i。
- 然后从这个位置i往后找最小的比他大的数字，交换。
- 然后将i之后的数字反转即可。
-
提交结果
558. 四叉树交集
二进制矩阵中的所有元素不是 0 就是 1 。
给你两个四叉树，quadTree1 和 quadTree2。其中 quadTree1 表示一个 n * n 二进制矩阵，而 quadTree2 表示另一个 n * n 二进制矩阵。
请你返回一个表示 n * n 二进制矩阵的四叉树，它是 quadTree1 和 quadTree2 所表示的两个二进制矩阵进行 按位逻辑或运算 的结果。
注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。
四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：
- val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
- isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。
我们可以按以下步骤为二维区域构建四叉树：
-
如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
-
如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然如下图所示，将当前网格划分为四个子网格。
-
使用适当的子网格递归每个子节点。
如果你想了解更多关于四叉树的内容，可以参考 wiki 。
四叉树格式：
输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。
它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。
如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。
-
解答
public Node intersect(Node quadTree1, Node quadTree2) { if(quadTree1.isLeaf){ if(quadTree1.val){ return quadTree1; }else{ return quadTree2; } }else{ if(quadTree2.isLeaf){ if(quadTree2.val) return quadTree2; else return quadTree1; }else{ Node topLeft = intersect(quadTree1.topLeft,quadTree2.topLeft); Node topRight = intersect(quadTree1.topRight,quadTree2.topRight); Node bottomLeft = intersect(quadTree1.bottomLeft,quadTree2.bottomLeft); Node bottomRight = intersect(quadTree1.bottomRight,quadTree2.bottomRight); if(topLeft.isLeaf && topLeft.val && topRight.isLeaf && topRight.val && bottomLeft.isLeaf && bottomLeft.val && bottomRight.isLeaf && bottomRight.val){ return new Node(true,true,null,null,null,null); } return new Node(true,false,topLeft,topRight,bottomLeft,bottomRight); } } } -
分析
- 若1结点是叶子结点，并且1结点的值为true，则直接返回1结点。否则返回2结点。
- 若2结点是叶子结点，并且2结点的值为true，则直接返回2结点，否则返回1结点。
- 若都不是叶子结点，则递归的去判断4个孩子结点，
- 若4个孩子结点都是叶子结点，并且值都为true，则合并
-
提交结果
559. N 叉树的最大深度
给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。
提示：
-
树的深度不会超过 1000 。
-
树的节点数目位于 [0, 104] 之间。
-
解答
public int maxDepth(Node root) { if(root == null)return 0; List<Node> list = new ArrayList<>(); list.add(root); int res = 0; while(list.size()>0){ res++; List<Node> temp = new ArrayList<>(); int index =0; while(index < list.size()){ Node cur = list.get(index++); temp.addAll(cur.children); } list = temp; } return res; } -
分析
- 层次遍历
-
提交结果
560. 和为K的子数组
给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。
-
解答
//方法1 public int subarraySum(int[] nums, int k) { int count = 0; for (int start = 0; start < nums.length; ++start) { int sum = 0; for (int end = start; end >= 0; --end) { sum += nums[end]; if (sum == k) { count++; } } } return count; } //方法2 public int subarraySum(int[] nums, int k) { Map<Integer,Integer> map = new HashMap<>(); int preSum = 0; int res = 0; map.put(0, 1); for(int i = 0;i < nums.length;i++){ preSum += nums[i]; res += map.getOrDefault(preSum - k,0); map.put(preSum,map.getOrDefault(preSum,0) + 1); } return res; } -
分析
-
方法1 暴力前缀和。
-
方法2 前缀和+hashMap优化
此题在乎的是连续的子数组的个数，并不需要具体的组合情况，所以可以用map来记录前缀和对应的前缀和出现的次数。
-
一次遍历得到每一步的前缀和preSum
-
那么此时需要考虑前面有多少个前缀和为preSum - k的组合。
-
因为 preSum - (preSum - k) = k。这样就可以得到基于当前的前缀和计算出有多少个联系的子数组 可以构成k。
-
维护map 前缀和的个数。
-
-
提交结果
方法1
方法2
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
