二叉树和递归

LeetCode 104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

  public class Main {
    public class TreeNode {
        int val;
      TreeNode left;
      TreeNode right;
      TreeNode(int x) { val = x; }
  }
  public int maxDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
    }

}

leetCode 226:反转二叉树

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        invertTree(root.right);
        invertTree(root.left);
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        return root;
    }
}

注意：如下写法是错误的

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        root.left = invertTree(root.right);
        root.right = invertTree(root.left);
        return root;
    }
}

这是因为左右子树的反转是不同步的，先执行了右子树的反转，结果给了左节点，然后再反转左子树的时候，实际上传入的是反转后的右子树的根节点

leetCode 112: 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 
给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if(root == null){
            return false;
        }
        if(root.left == null && root.right == null){
            return root.val == sum;
        }
        return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val);
    }
}

257：二叉树中的所有路径

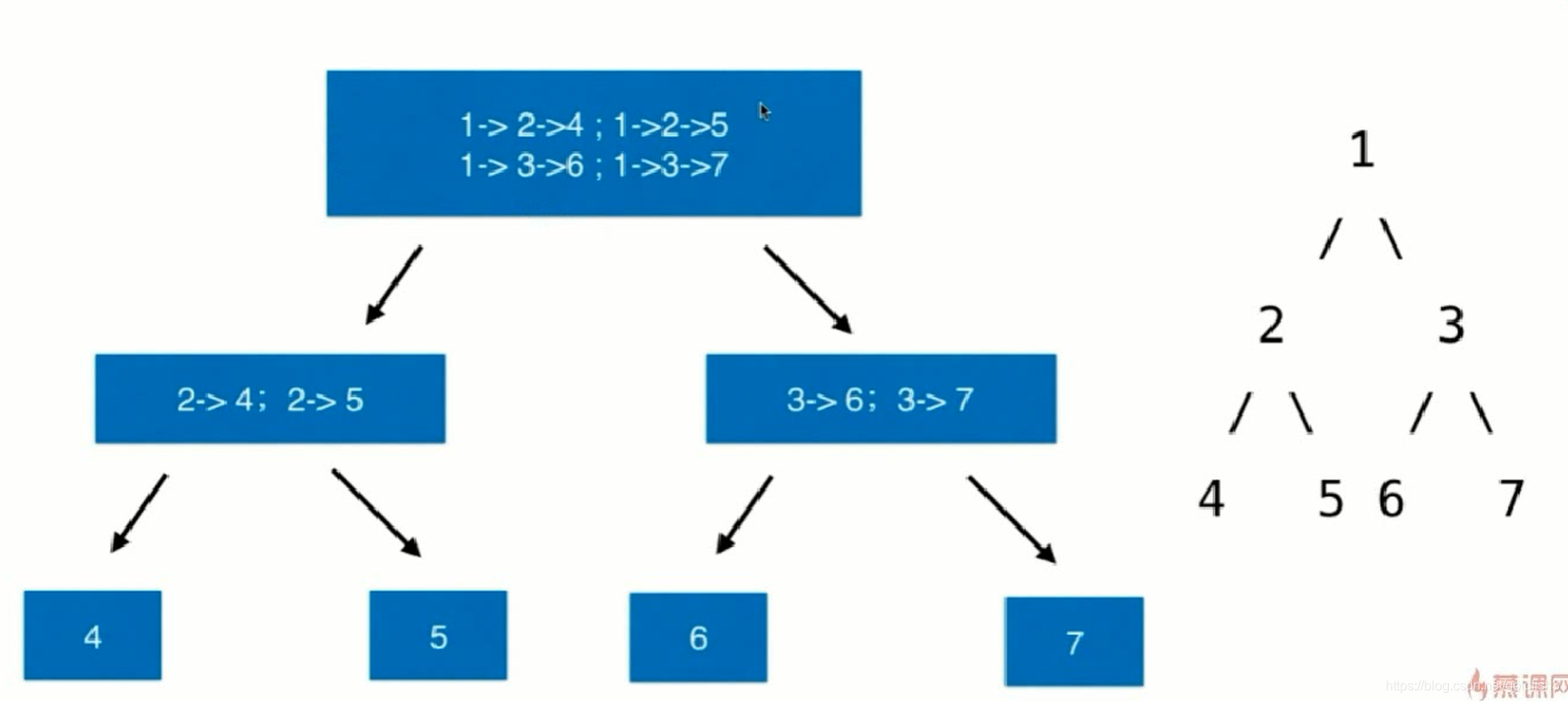
public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new LinkedList<String>();
        if (root == null){
            return res;
        }
        if (root.left == null && root.right == null){
            res.add(String.valueOf(root.val));
            return res;
        }
        //将左子树的所有元素和当前节点结合
        if (root.left != null){
            List<String> leftRes = binaryTreePaths(root.left);
            for (int i=0; i<leftRes.size(); i++){
                res.add(String.valueOf(root.val) + "->" + leftRes.get(i));
            }
        }
        //将右子树的所有元素和当前节点结合
        if (root.right != null){
            List<String> rightRes = binaryTreePaths(root.right);
            for (int i=0; i<rightRes.size(); i++){
                res.add(String.valueOf(root.val) + "->" + rightRes.get(i));
            }
        }
        return res;
    }

437. 路径总和 III

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

返回 3。和等于 8 的路径有:

1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11

错误解法

public int pathSum(TreeNode root, int sum) {
        int count = 0;
        if (root == null){
            return 0;
        }
        count += pathSum(root.left, sum);
        count += pathSum(root.right, sum);
        count += pathSum(root.left,sum - root.val);
        count += pathSum(root.right,sum - root.val);
        return count;
    }

这里

count += pathSum(root.left,sum - root.val);
count += pathSum(root.right,sum - root.val);

求的是以当前节点为根的子树，和为 sum-root.val，这其实是没有意义的，因为递归到当前节点的sum值可能来自于

count += pathSum(root.left, sum);
count += pathSum(root.right, sum);

而这两句代码没有考虑节点本身的值
比如和为7，当前节点为3，左子树的左子树，为4，用面的方法是可以得出7，但是没有意义，因为左子节点并没有被计算。
递归要求以一种模式运行，但是上面存在两种模式
正确解法
将另外一种模式单独拆出来，做为一个递归

public class Main {
    public class TreeNode {
        int val;
      TreeNode left;
      TreeNode right;
      TreeNode(int x) { val = x; }
  }

    public static void main(String[] args) {

    }

    public int pathSum(TreeNode root, int sum) {
        int count = 0;
        if (root == null){
            return 0;
        }
        count += pathSum(root.left, sum);
        count += pathSum(root.right, sum);
        count += pathSum2(root,sum);
        return count;
    }

    //包含当前节点和为sum
    public int pathSum2(TreeNode node, int sum){
        if (node == null){
            return 0;
        }
        int res = 0;
        if (node.val == sum){
            res++;
        }
        res += pathSum2(node.left,sum - node.val);
        res += pathSum2(node.right, sum - node.val);
        return res;
    }
}

leetCode:235 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

-
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p == null || q == null){
            return null;
        }
        if(p.val < root.val && q.val < root.val){
            return lowestCommonAncestor(root.left, p, q);
        }
        if(p.val > root.val && q.val > root.val){
            return lowestCommonAncestor(root.right, p, q);
        }
        return root;
    }
}