混合动力重卡实时能量管理

基于序列规划的混合动力重型车辆实时预测性能量管理

摘要

为了降低燃油消耗，本文提出了一种针对混合动力重 型车辆的实时预测性能量管理方法。我们提出了一种最优控制策 略，用于确定不同车辆动力源与制动器之间的功率分配。基于模 型预测控制（MPC）和序列规划，针对长度为5‐20公里的前方 路段，求解车辆速度和电池荷电状态的最优轨迹。随后，调节加 速和制动踏板位置以及电池使用情况，以跟踪请求速度和荷电状 态，并通过高保真车辆系统模型进行了验证。本文的主要贡献是 开发了一种用于预测性能量管理的序列线性规划方法，相比测试 求解器中的序列二次规划，该方法更快、更简单，且所生成的轨 迹接近非线性规划所得的最佳轨迹。本文还对该方法与两种不同 的序列二次规划方法的性能进行了比较。

索引术语

预测性能量管理策略；混合动力重型车辆；最优 控制；序列线性规划

一、引言

日益增长的环境和全球变暖问题，以及相关法规和消 费者期望，推动了道路运输减排新解决方案的发展。根据 [1],，重型车辆在欧洲道路交通的CO2排放中占25%。
在各种减排方案中，基于道路地形数据的能量管理控制策 略已被证明可有效降低传统重型车辆的燃油消耗 [2],[3][4]。此处的挑战在于高效求解可在车载系统上实 时实施的最优控制问题，以获得车辆速度的最优轨迹
并确定了档位。在[5],中提出了一种基于动态规划（ DP）的高效算法，用于车辆速度和挡位选择的最优控制。
尽管传统车辆的燃油效率近年来有所提高，但由于道 路货运交通量不断增加，道路交通排放仍在上升，如[1]所 述。此外，根据欧盟法规（EU）2018/842，与2019年相 比，新型重型车辆的CO2排放量需在2025年和2030年分 别减少15%和30%，这迫使必须部署纯电动和混合动力重 型车辆，以进一步降低道路交通带来的排放，并实现环保 目标。
纯电动汽车的能量管理问题与传统车辆类似，其唯一 的动态状态是车辆速度。然而，对于混合动力汽车（ HEV），由于存在多个动力源，能量管理问题更加复杂。
在这类车辆中，再生制动能量可以被储存，并在内燃机 （ICE）关闭时使用，或用于帮助发动机运行于更优的工 况条件下。混合动力汽车得益于最优能量管理，即根据前 方道路信息确定转速、不同动力源的功率使用以及换挡选 择的最优轨迹。因此，混合动力汽车的最优控制问题规模 大于传统车辆，使其高效求解更具挑战性。
针对混合动力汽车（HEV）的最优控制问题，已开 展了多项研究。文献中研究的基于模型的求解方法包括基 于庞特里亚金极小值原理（PMP）和动态规划（DP）的 策略。这些策略还可根据问题的动态状态、所采用的简化 方法以及离线与在线方法进行分类。采用PMP的方法通 常为在线方法，其试图通过利用必要最优性条件来推导解 析解。在混合动力汽车能量管理领域一个著名的例子是等 效燃油消耗最小策略（ECMS）[6],，该方法将原问题中 的电池荷电状态替换为其对偶变量。原始动态问题随后被 转化为两点边值问题，可通过单次打靶法高效求解。然而， 当问题中状态约束频繁激活或需要整数决策时，PMP的 计算优势会减弱。对于频繁激活约束或存在整数决策的问 题，通常采用直接转录方法进行处理，然后求解
数值上。常见的例子包括用于平滑非线性规划的多重打靶 法和配置方法 [7],[8]，以及用于混合整数规划的动态规 划（DP）和分支定界割平面技术 [9],[10],[11] ，这些 方法通过将速度优化与功率分配和换挡优化解耦，或假设 速度曲线已预先知晓来实现。
动态规划（DP）也是混合动力汽车能量管理中常用的一 种方法[12],[13]，当状态数大于一时，其计算量较大，因此 在该情况下主要适用于离线实现。文献[6]针对固定速度曲 线对庞特里亚金极小值原理（PMP）和动态规划（DP）进 行了比较。
然而，将速度优化与电池使用控制相结合至关重要。
如[14],所述，速度曲线会影响混合动力汽车最优能量管 理。利用前方路段信息对车辆速度进行优化的一个直观示 例是：在下坡路段仅利用重力使车辆加速，同时关闭发动 机。如果车辆在到达下坡路段前已经具有较高速度，则其 利用重力的能力会降低，因为车速不能超过法定最高速度， 从而必须使用制动器。若能在进入下坡路段之前适当降低 车辆速度，则可避免使用制动器。在混合动力汽车中，再 生制动也并非最佳选择，因为轮到轮能量效率（即通过再 生制动产生的电能储存至电池并用于推进的效率）通常低 于75%。因此，相比电力推进，应优先考虑利用重力来提 高车辆速度。因此，将速度视为动态状态并对其速度曲线 进行优化，会对混合动力汽车的能量管理产生影响，且该 影响与功率分配和换挡优化相互耦合。此外，在能量管理 中引入速度优化有助于车辆对交通扰动做出最优响应。
对于包含两个或更多连续状态的问题，在线控制策略包括 预测未来驾驶循环的随机动态规划（DP）[15]，以及同时优化 速度、荷电状态（SOC）、发动机启停和换挡曲线的模型预测 控制，后者可通过结合直接法（即凸优化和动态规划（DP） [16],[17],）或结合动态规划（DP）和庞特里亚金极小值原理 （PMP）[18]实现。不同方法的综述可参见[19]和[20]。
解决和验证混合动力汽车（HEV）预测性能量管理的 实际问题具有挑战性。在此类问题中，成本函数可能包含 燃油和电能成本、电池和摩擦制动磨损以及驾驶舒适性等 组成部分。系统状态可通过车速、传动比、电池能量和发 动机启停状态或与这些特性相关的其他变量来描述，从而 构成动态状态变量。此外，控制变量可能包括内燃机功率 请求、不同车轴上的电机（EM）功率请求、档位及制动 功率请求，具体取决于动力总成自由度。综合所有这些状 态和控制变量将导致一个动态的、混合整数且非线性的最 优控制问题。
这是一个在实时情况下很难解决的问题。在本论文中，相 反地，该问题被划分为三个具有不同时域和更新频率的控 制层，使我们能够使用代表实际车辆的高保真复杂整车模 型来测试该算法。
本文提出采用序列线性规划（SLP）而非文献 [16],[17],[21]中提出的序列二次规划（SQP），以求解 车辆速度和荷电状态（SOC）以及连续和离散输入的最优 轨迹。使用SLP的主要优势在于，对于所测试的求解器 （如Gurobi），其计算速度平均比SQP快4倍，适用于不 同的预测时域长度。本文从单次序列计算速度、收敛前的 迭代次数以及所得最优轨迹等方面，对SLP与SQP的性能 进行了比较。此外，在SLP中，成本函数和约束被依次更 新，以消除线性化误差。另外，本文提出了两种略有不同 的SQP方法，与以往文献中的方法有所不同。在第一种 SQP方法中，通过提取二次近似的海森矩阵的半正定部分， 在顺序迭代过程中不断更新燃油消耗率测量数据的凸近似， 以确保凸性。在第二种SQP方法中，燃油消耗率的二次近 似函数在顺序迭代过程中不进行更新，但选择二次近似中 的项，使得对于给定的测量数据，近似始终保持凸性，从 而实现更好的拟合效果；即与使用二次近似处理一般非线
性燃油消耗率测量数据的类似研究[22],[16],[23],[21]
相比，该凸近似与测量数据的接近程度提高了34%。然而， 第二种SQP方法无法消除顺序迭代过程中燃油消耗率近似 带来的误差。尽管如此，它相较于第一种SQP方法需要更 少的计算量，并避免了对噪声数据的过拟合。
在所有这三种方法中，状态包括速度、电池能量和时 间，同时存在离散控制变量，即挡位和发动机启停。离散 控制变量通过在第一控制层的每次顺序迭代中求解一个次 级优化子问题来处理。虽然换挡优化子问题不具备预测性， 但它受到换挡速率的约束。可以用预测性最优控制子问题 （例如使用动态规划（DP）方法，如[16],[17],[24]中 所述）替代瞬时换挡优化子问题，但这会增加计算量。此 外，在本论文中，发动机启停状态被纳入换挡选择中，其 中零挡位表示发动机不工作，而其他任何挡位数值均表示 发动机处于运行状态。
论文其余部分的结构如下。第二节介绍了车辆模型以 及非线性混合整数最优控制问题。第三节概述了求解方法， 包括控制层级和序列化线性与二次规划。第四节展示了结 果。最后，第五和第六节分别对研究进行了讨论并总结了 全文。

II. 问题描述

A. 车辆模型

车辆被建模为具有车轮的集中质量，车轮存在滚动阻 力。在时间 t时车轮处的总力 Fw(t)由以下公式给出
$$
F_w(t) = m\dot{v}(t) + mg \sin \alpha(s(t)) + mgf_r \cos \alpha(s(t)) + 0.5\rho_a A_f c_d v(t)^2, \quad (1)
$$
其中， $m$为车辆总质量或等效总质量，$v$为车辆纵向速 度，公式(1)右侧的最后三项分别表示道路坡度、滚动阻
力（建模为体作用力）和空气阻力； $g$、 $\alpha$、 $f_r$、 $\rho_a$、 $s(t)$、 $A_f$和 $c_d$分别为重力加速度、道路坡度、时间t时的 行驶距离、滚动阻力系数、空气密度、车辆等效前部面积 和空气阻力系数。
然后，车辆加速以及在车轮处补偿阻力所需的总功率 $P_w(t)$由下式给出
$$
P_w(t) = F_w(t)v(t). \quad (2)
$$

图1展示了本文所使用的并联式混合动力传动系统以 及不同传动系统子系统之间的能量流（即功率）。在该图
中，在某一时刻或给定的时间区间内，对于柴油推进， $P_f$、
$P_e$、 $P_{de}$、 $P_{ew}$和 $P_{det}$分别表示燃料功率、内燃机输出 的功率、内燃机中耗散的功率、内燃机传动输出的功率以
及内燃机传动中耗散的功率。在电力推进侧， $P_b$、 $P_{db}$和
$P_a$分别表示电池提供或储存的功率、电池中耗散的功率
以及用于辅助设备的功率，而 $P_{mc}$ 、 $P_{dm}$ 、 $P_m$ 、 $P_{dmt}$
和 $P_{mw}$ 分别表示电动机消耗或再生的功率、电动机中耗 散的功率、电动机输出/输入至/自传动系统的功率、电机
传动中耗散的功率以及输出/输入至/自车轮的功率， $P_{br}$
为摩擦制动。
功率。本文所使用的传动系统中未对惯性飞轮或弹性轴进 行建模。因此，对于每个传动系统子系统，可以假设其功 率平衡，因为除燃油箱和电池外，传动系统内部不存储也 不产生能量。例如，内燃机变速器、车轮和电机传动系统 的能量平衡可表示为
$$
P_{ew} + P_{det} - P_e = 0 \quad (3a) \
P_w + P_{br} - P_{ew} - P_{mw} = 0 \quad (3b) \
P_{mw} + P_{dmt} - P_m = 0, \quad (3c)
$$
其中，如果能量从子系统流出，则能量流为正，例如所有耗散 项均为正。
为提高可读性，公式(3)中省略了函数参数。通常情 况下，传动系统部件的损耗是转速、部件功率、所选内燃 机挡位 $\gamma_e$或电机挡位 $\gamma_m$的非线性函数。此外，值得注意 的是，未对停止和倒车情况进行建模，且忽略了描述传动 系和车轮中旋转部件惯性以及轮胎滑移导致的能量损失的 项。然而，可通过使用等效附加质量来考虑旋转部件的惯 性。
测量数据可用于描述内燃机和电动机在不同扭矩和角 速度下的功率损耗。这些数据可直接从映射图中读取，或 通过高阶非线性曲线进行拟合。内燃机和电动机的扭矩与 角速度与其功率及车速相关，具体关系如下
$$
\omega_e(t) = \frac{r_e(\gamma_e(t))}{R_w} v(t), \quad T_e(t) = \frac{1}{\omega_e(t)} P_e(t), \quad (4) \
\omega_m(t) = \frac{r_m(\gamma_m(t))}{R_w} v(t), \quad T_m(t) = \frac{1}{\omega_m(t)} P_m(t), \quad (5)
$$
其中， $R_w$、 $r_e$、 $T_e$ 和 $\omega_e$ 分别表示车轮半径、从车轮到 发动机的传动比、发动机扭矩和发动机转速，类似地，对于 电动机， $r_m$、 $T_m$ 和 $\omega_m$ 分别表示从车轮到电动机的传动 比、电机扭矩和转速。公式(4) 和 (5) 在空挡时不适用。
测量数据可通过一个关于内燃机燃料能量速率 $E_f = P_f$
和电机消耗功率 $P_{mc}$的阶数为 $n$的多项式曲面$\dot{}$进行拟合； 然而，其他任何曲面拟合函数也可能是有效的。
$$
P_f(\omega_e(t), T_e(t)) = \sum_{i=0}^{n} \sum_{j=0}^{n} a_{ij} \omega_e(t)^i T_e(t)^j, \quad (6) \
P_{mc}(\omega_m(t), T_m(t)) =
\begin{cases}
\sum_{i=0}^{n} \sum_{j=0}^{n} h^+ {ij} \omega_m(t)^i T_m(t)^j, & T_m(t) > 0, \
\sum {i=0}^{n} \sum_{j=0}^{n} h^- {ij} \omega_m(t)^i T_m(t)^j, & T_m(t) \leq 0,
\end{cases} \quad (7)
$$
其中 $a {ij}$ 、 $h^+ {ij}$ 和 $h^- {ij}$ 表示拟合函数的系数。图2显示了 测量值和发动机燃料能量率的5阶多项式曲面拟合。

-400 -200 0 200 400 600
扭矩（牛·米）
Power consumption
100 转/分钟
1500 转/分钟 2900 转/分 4300 转/分 5700 转/分
7100 转/分
8500 转/分 9900 转/分 测量值
拟合值

图3. 基于实验测量的电动机功率消耗 Pmc与扭矩和转速的关系。
正负扭矩由5次曲面拟合。
使用高阶数的拟合曲面可相对准确地近似测量数据。类似 地， $P_{mc}$的拟合曲面如图3所示，其中正负扭矩的测量数 据通过两个不同的曲面进行拟合，以确保电机扭矩和电机 消耗功率 $P_{mc}$具有相同的符号。电机中的功率损耗的原 始测量数据基于机械效率。从效率图到消耗功率图的转换 在附录中说明。
可以假设电池具有恒定的开路电压 $V_b$和电阻 $R$， 而由于电池内阻引起的电压降可忽略不计[23]。
$$
P_{db}(P_{mc}(t), P_a(t)) = \frac{R}{V_b^2}(P_{mc} + P_a)^2. \quad (8)
$$
此外，在本论文中，传动损耗是输入功率的线性函数， 与换挡选择无关，因此，
$$
P_{det}(P_e(t)) = P_e(t) - \eta_{te}P_e(t), \quad P_e(t) \geq 0, \quad (9)
$$
and
$$
P_{dmt}(P_m(t)) =
\begin{cases}
P_m(t) - \eta_{tm}P_m(t), & P_m(t) > 0 \
-(\eta_{tm}^{-P_m(t)}), & P_m(t) \leq 0,
\end{cases} \quad (10)
$$
其中 $\eta_{te}$表示发动机的传动效率， $\eta_{tm}$表示电动机的传动
效率。耗散功率 $P_{dmt}$始终为正值，因此公式(10)的第二 部分需要添加负号。
还必须考虑动力总成部件在转换能量（或功率、力和 扭矩）时的限制。发动机和电动机中的扭矩限制及其分段 拟合曲线如图4所示。每一段的阶数为 $n$的多项式拟合曲 线由以下给出
$$
T_{li}(\omega(t)) = \sum_{j=0}^{n} b_{ij} \omega(t)^j, \quad i = 1,…, 4, \quad (11)
$$
其中 $T_l$表示扭矩限制拟合曲线， $b_i$是多项式系数。
电池容量和功率也有限。电池SOC由下式给出
$$
soc(t_f) = soc(t_0) - \frac{1}{E_{bmax}} \int_{t_0}^{t_f} P_b(t)dt, \quad (12)
$$
where $E_{bmax}$是电池的最大能量容量 acity

B. 预测性能量管理的非线性和混合整数问题

本文中的非线性混合整数最优控制问题定义如下。
Find $u_c(s) \in \mathbb{R}^{n_{cc}}, u_d(s) \in \mathbb{N}^{n_{cd}}$
to minimize
$$
J = C(x(s_0), x(s_f)) + \int_{s_0}^{s_f} L(x(s), u(s), s)ds \quad (13a)
$$
受以下条件约束
$$
\frac{dx(s)}{ds} = f(x(s), u(s), s), \quad x(s) \in \mathbb{R}^{n_s} \quad (13b) \
x(s_0) = x_0 \quad (13c) \
x(s_f) = x_f \quad (13d) \
g(x(s), u(s), s) \leq 0, \quad (13e)
$$
其中 $x$表示 $n_s$状态， $u = [u_c, u_d]$表示 $n_{cc}$连续和
$n_{cd}$离散控制变量， $J$、 $C$、 $s_0$、 $s_f$和 $L$分别表示成本 函数、初期和终止状态的成本、初始位置、终止位置和阶 段成本函数。动态模型方程由约束方程(13b)‐(13d)给出。
最后，约束方程(13e)限制了动力总成部件的能力以及界 限状态和控制变量。在上述最优控制问题中，可以使用除 位置 $s$之外的任何其他独立变量。
在混合动力汽车预测性能量管理的情况下，道路坡度轮 廓由位置描述，因此更容易

发动机，其中拟合曲线为 Tle1‐Tle4；b) 电动机，其中拟合曲线为 Tlm1‐Tlm4)
描述相对于行驶距离而非时间的最优控制问题和车辆模型， 因为这样可以消除道路坡度作为位置函数在最优控制问题 中的非线性。此外，这有助于避免由于行驶距离上道路限 速的突变所引起的混合整数问题，因为在时域中对速度限 制的阶跃变化进行建模会导致混合整数问题。从时间到行 驶距离的转换 $s$通过积分实现
$$
dt = \frac{ds}{\bar{v}(s)}, \quad \bar{v}(s) = v(t). \quad (14)
$$
基本上， $\bar{v}(\cdot)$ 和 $v(\cdot)$ 是不同的函数；但为了符号表示的简洁， ¯ 将从后续方程中省略。
此外，功率 $P$、能量 $E$、力 $F$、扭矩 $T$ 和速度 $v$ 之间的关系由以下给出。
$$
P(s) = \frac{dE(s)}{dt} = v(s) \frac{dE(s)}{ds} = v(s)F(s) = \omega(s)T(s). \quad (15)
$$
状态包括车辆速度 $v$、电池SOC $soc$和行驶时间 $t$， 即 $x=[v, soc, t]$。必须将行驶时间作为状态引入，因为需 要进行时间计算以约束总行程时间，而其他方程则与时间
无关。此外，控制变量为等效发动机输出力 $F_e = \frac{dE_e(s)}{ds}$、
电动机在车轮上的作用力 $F_{mw} = \frac{dE_{mw}(s)}{ds}$、车轮上的制
动力 $F_{br} = \frac{dE_{br}(s)}{ds}$、内燃机的整数档位 $\gamma_e$以及电动机
的整数档位 $\gamma_m$，分别为 $u_c =[F_e, F_{mw}, F_{br}]$和
$u_d =[\gamma_e, \gamma_m]$。因此，基于车辆模型，混合动力汽车能量 管理的非线性混合整数最优控制问题可定义如下。值得注 意的是，以下问题不包含任何离散状态。本节下文给出了 该问题以方程(13)形式表示的紧凑形式，其中所有代数方 程均已针对状态和控制变量求解。
论文的
Find $F_e(s), F_{mw}(s), F_{br}(s), \gamma_e(s), \gamma_m(s)$
最小化
$$
J_{nl} = \int_{s_0}^{s_f} (F_f(\cdot) + F_{br}(s) + F_{del}(s))ds \quad (16a)
$$
约束条件
$$
F_w(s) = mv(s) \frac{dv(s)}{ds} + mg \sin \alpha(s) + mgf_r \cos(\alpha(s)) + 0.5\rho_a A_f c_d v(s)^2 \quad (16b) \
\frac{dsoc(s)}{ds} = -\frac{F_b(s)}{E_{bmax}} \quad (16c) \
\frac{dt(s)}{ds} = \frac{1}{v(s)} \quad (16d) \
v(s_0) = v_0, \quad soc(s_0) = soc_0, \quad t(s_0) = t_0 \quad (16e) \
soc(s_f) = soc_f \quad (16f) \
F_w(s) + F_{br}(s) - F_{ew}(s) - F_{mw}(s) = 0 \quad (16g) \
F_{ew}(s) = \eta_{te} F_e(s) \quad (16h) \
F_b(s) = F_{mc}(s) + F_{db}(s) + F_a(s) \quad (16i) \
F_{db}(s) = \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2 \quad (16j) \
F_{mc}(s) =
\begin{cases}
\frac{1}{v(s)} \sum_{i=0}^{5} \sum_{j=0}^{5} (h^+ {ij} (\frac{r_m(\gamma_m(s))}{R_w} v(s))^i (\frac{R_w}{r_m(\gamma_m(s))} F_m(s))^j), & F {mw}(s) > 0 \
\frac{1}{v(s)} \sum_{i=0}^{5} \sum_{j=0}^{5} (h^- {ij} (\frac{r_m(\gamma_m(s))}{R_w} v(s))^i (\frac{R_w}{r_m(\gamma_m(s))} F_m(s))^j), & F {mw}(s) \leq 0
\end{cases} \quad (16k) \
F_{del}(s) = F_{dmt}(s) + F_{dm}(s) + F_{db}(s) \quad (16l) \
F_{dm}(s) = F_{mc}(s) - F_m(s) \quad (16m) \
F_{dmt}(s) = F_m(s) - F_{mw}(s) \quad (16n) \
F_m(s) =
\begin{cases}
\frac{F_{mw}(s)}{\eta_{tm}}, & F_{mw}(s) > 0 \
\eta_{tm} F_{mw}(s), & F_{mw}(s) \leq 0
\end{cases} \quad (16o) \
\frac{R_w}{r_e(\gamma_e(s))} F_e(s) \leq \min \left{ \sum_{j=0}^{3} b^e_{ij} \left( \frac{r_e(\gamma_e(s))}{R_w} v(s) \right)^j, i=1,…,4 \right} \quad (16p) \
\frac{R_w}{r_m(\gamma_m(s))} F_m(s) \leq \min \left{ \sum_{j=0}^{3} b^m_{ij} \left( \frac{r_m(\gamma_m(s))}{R_w} v(s) \right)^j, i=1,2 \right} \quad (16q) \
-\frac{R_w}{r_m(\gamma_m(s))} F_m(s) \leq -\max \left{ \sum_{j=0}^{3} b^m_{ij} \left( \frac{r_m(\gamma_m(s))}{R_w} v(s) \right)^j, i=3,4 \right} \quad (16r) \
t(s_f) \leq t_{tref} \quad (16s) \
soc(s) \in [soc_{min}, soc_{max}] \quad (16t) \
v(s)F_b(s) \in [p_{bmin}, p_{bmax}] \quad (16u) \
v_{min}(s) \leq v(s) \leq v_{max}(s) \quad (16v) \
0 \leq F_e(s) \quad (16w) \
0 \leq F_{br}(s). \quad (16x)
$$
公式(16a)中的成本函数 $J_{nl}$是非线性的，其最小化 代表了输入发动机能量（即燃料 $E_f$）以及电动机 $E_{del}$和 制动器 $E_{br}$上耗散的能量的最小化，从而最小化它们的使 用。将电动机中耗散的能量 $E_{del}$包含在成本函数中，是 为了使后续对电机能量损耗进行线性化成为可能，如后文 所述。虽然制动能量$E_{br}$不必包含在成本函数中，但它有 助于加快非线性规划、SQP和SLP的收敛速度。
$F_f$ 是等效发动机燃油力，可通过以下方法获得。利 用公式(4)和(6)，结合 $n= 5$ 阶表面拟合以及变量从时间 到空间的变换，可推导出燃料能耗对行驶距离的导数（即 等效燃油力）。
$$
F_f(F_e(s), v(s), \gamma_e(s), s) = \frac{dE_f(F_e(s), v(s), \gamma_e(s), s)}{ds} = \frac{1}{v(s)} \sum_{i=0}^{5} \sum_{j=0}^{5} a_{ij} \left( \frac{r_e(\gamma_e(s))}{R_w} v(s) \right)^i \left( \frac{R_w}{r_e(\gamma_e(s))} F_e(s) \right)^j. \quad (17)
$$
此外，公式(16b)、(16c)和(16d)分别为等效于公式
(1)、(12)和(14)的动态方程或状态方程。公式(16e)‐(16f)
分别确定状态的初始值和最终值。公式(16g)表示车轮上 的力平衡，其中 $F_{ew}$表示内燃机传动输出端的等效力。
公式(16h)考虑了内燃机传动系统中的能量耗散。公式 (16i)表示电池中的等效力平衡，其中 $F_{mc}$表示由公式 (16k)给出的电池与电机之间的等效力，该式还考虑了电 机在正负扭矩下的损耗，类似于公式(7)， $F_{db}$是由公式 (16j)给出的电池中耗散的等效力， $F_a$为给定的辅助力。
公式(16l)‐(16o)表示电驱动系统中耗散的等效力 $F_{del}$， 其可通过公式(3)、(15)、(7)、(8)、(10)和(5)推导得出，
其中 $F_{dm}$和 $F_{dmt}$分别表示在电机和电机传动系统中耗散 的等效力。公式(16p)、(16q)和(16r)对图4所示的内燃机 和电机的扭矩施加限制。总行程时间通过公式(16s)约束
为等于或小于参考行程时间 $t_{tref}$，获取参考行程时间的方 法在附录中说明。电池能量水平约束通过在(16t)中限制电 池SOC $soc$来实现。公式(16u)和(16v)分别限制电池功率 和车辆速度，最后，公式(16w)和(16x)分别对内燃机等效 力和制动力施加下限约束。
通过求解控制变量的代数约束并进行回代，得到以方 程(13)形式表示的方程(16)的紧凑形式。
Find $F_e(s), F_{mw}(s), F_{br}(s), \gamma_e(s), \gamma_m(s)$
以最小化
$$
J_{nl} = \int_{s=s_f}^{s=s_0} (F_f(\cdot) + F_{br}(s) - F_{mw}(s) + \quad (18a) \
F_{mc}(s) + \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2)ds
$$
受限于
$$
f_1: \frac{dv(s)}{ds} = \frac{1}{mv(s)} (F_{br}(s) - \eta_{te}F_e(s) - F_{mw}(s) - mg \sin \alpha(s) - mgf_r \cos \alpha(s) - 0.5\rho_a A_f c_d v(s)^2) \quad (18b) \
f_2: \frac{dsoc(s)}{ds} = -\frac{1}{E_{bmax}} \left( F_{mc}(s) + \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2 + F_a(s) \right) \quad (18c) \
f_3: \frac{dt(s)}{ds} = \frac{1}{v(s)} \quad (18d) \
v(s_0) = v_0, \quad soc(s_0) = soc_0, \quad t(s_0) = t_0 \quad (18e) \
soc(s_f) = soc_f \quad (18f) \
g_1: \frac{R_w}{r_e(\gamma_e(s))} F_e(s) - \min \left{ \sum_{j=0}^{3} b^e_{ij} \left( \frac{r_e(\gamma_e(s))}{R_w} v(s) \right)^j, i=1,…,4 \right} \leq 0 \quad (18g) \
g_3: -\frac{R_w F_{mw}(s)}{\eta_{tm} r_m(\gamma_m(s))} + \max \left{ \sum_{j=0}^{3} b^m_{ij} \left( \frac{r_m(\gamma_m(s))}{R_w} v(s) \right)^j, i=3,4 \right} \leq 0 \quad (18h) \
g_4: t(s_f) - t_{tref} \leq 0 \quad (18i) \
g_5: soc_{min} - soc(s) \leq 0 \quad (18j) \
g_6: soc(s) - soc_{max} \leq 0 \quad (18k) \
g_7: p_{bmin} - v(s) \left( F_{mc}(s) + \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2 + F_a(s) \right) \leq 0 \quad (18l) \
g_8: v(s) \left( F_{mc}(s) + \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2 + F_a(s) \right) - p_{bmax} \leq 0 \quad (18m) \
g_9: v_{min}(s) - v(s) \leq 0 \quad (18n) \
g_{10}: v(s) - v_{max}(s) \leq 0 \quad (18o) \
g_{11}: -F_e(s) \leq 0 \quad (18p) \
g_{12}: -F_{br}(s) \leq 0, \quad (18q)
$$
其中 $C(x(s_0), x(s_f)) = 0$，且 $F_{mc}$由公式(16k)给出。
可以考虑对加速度施加约束，但本文并未直接应用。
加速度和急动度的约束可在第二控制层中应用，以提高舒 适性。然而，在第一层中，这些约束通过最小化成本函数 间接实现，其中通过使用推进和制动能量来抑制加速和减 速。

III. 方法

A. 控制层

总体控制层级从上到下的结构如图5所示。该系统包 含三个具有不同更新频率的控制层。本论文的重点是第一 控制层。然而，本文在此处对其他控制层进行了简要描述， 以提供车辆推进控制系统的整体概述。

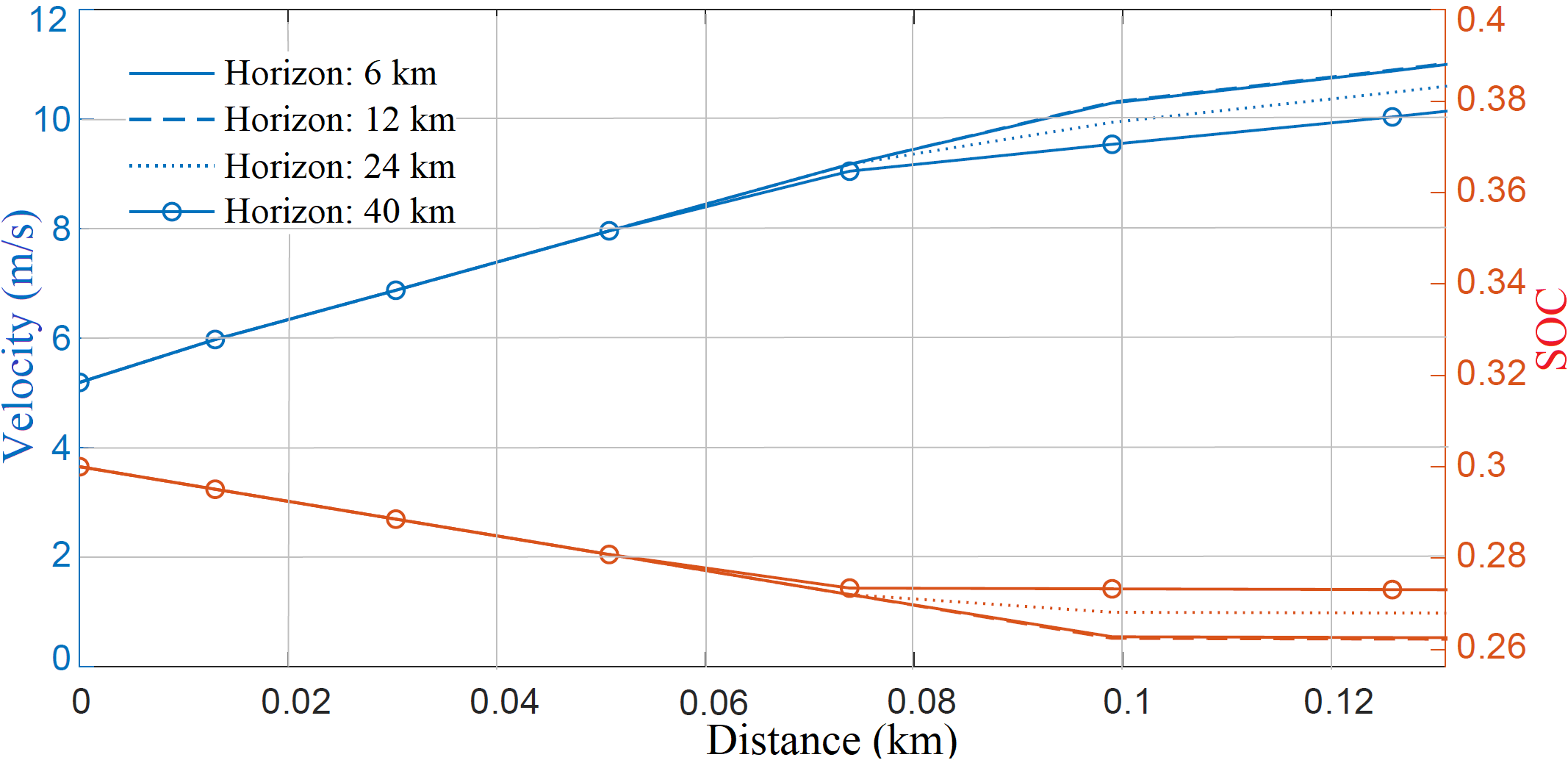
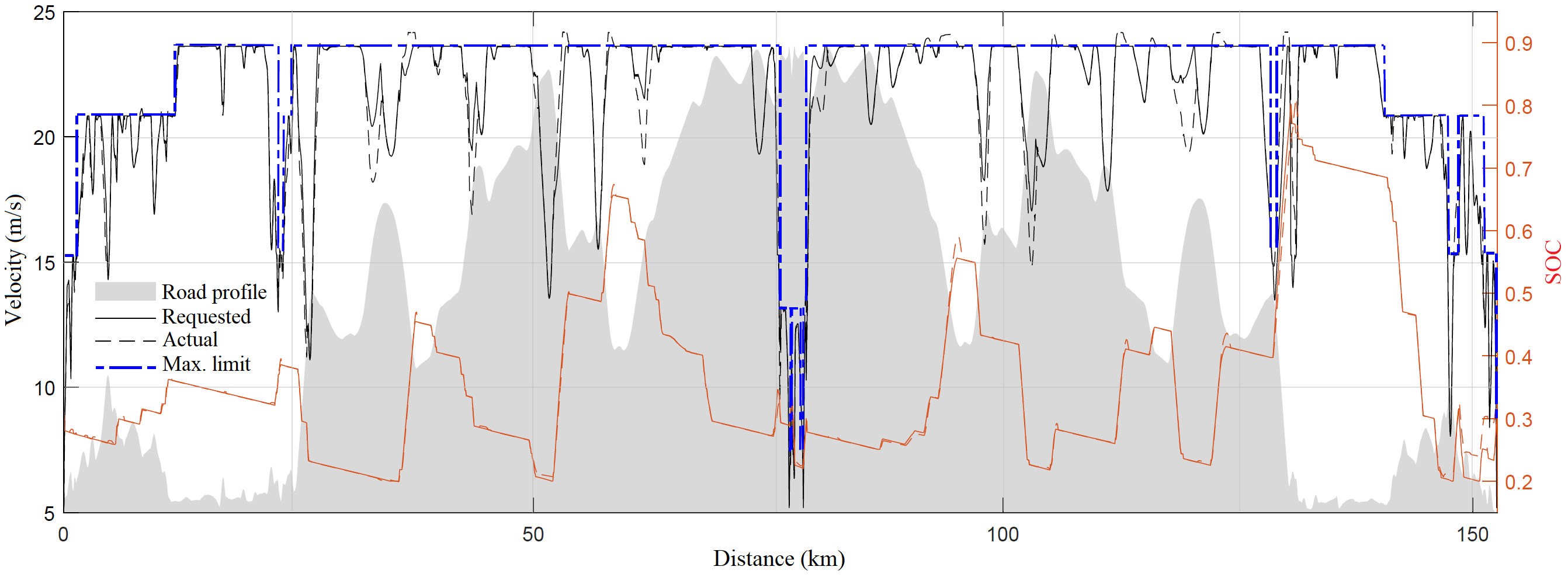
第一控制层利用前方长达20公里的周围环境信息，规 划车辆速度 $v_{req}$、电池能量 $soc_{req}$和挡位轨迹。周围环境 信息包括交通状况、地形学、道路曲率、车道、法定速度 限制、因交通引起的动态速度限制以及因道路曲率引起的 速度限制；本文中已包含道路地形和法定速度限制信息。
第一层的输出为请求速度、电池SOC和挡位轨迹，这些信 息被发送到第二层和第三层。挡位轨迹包括相当于内燃机 关闭的空挡状态。在第一层中，状态为速度、电池能量和 时间，控制变量为内燃机、电动机、制动力和挡位。基于 MPC理论，采用序列线性规划或序列二次规划方法求得 最优轨迹。挡位轨迹作为线性或二次规划的输入，在每次 顺序迭代中分别进行顺序优化，逐步收敛至次优轨迹，本 节后文将对此进行详细说明。
第二层和第三层对于补偿实际道路和车辆中无法通过 第一层所用模型描述的不完美性是必要的。第二层规划请 求推进功率$P_{prop,req}$和制动力$P_{prop,req}$，或等效地规划制 动和加速踏板位置。该层的主要目标是为车辆提供适当的 功率请求，以使其能够跟踪第一层提供的请求速度轨迹， 同时保证舒适性和效率。该层被实现为短时域MPC，类 似于文献[25]中提出的控制器。
最后，第三层负责设备执行的监控与控制。该层包括 电池能量的瞬时控制策略——特别是使用第一控制层生成 的参考SOC轨迹的等效燃油消耗最小策略[26],[27],[6], 。
值得注意的是，在测试高保真车辆动力学模型时，假 设车辆配备了自动变速箱，能够以最佳方式执行换挡选择。
因此，该变速箱可以覆盖来自第一层的换挡请求，但空挡 请求除外。

B. 使用顺序程序的预测性能量管理

顺序程序通过依次求解最优控制问题直至达到收敛。
首先，必须对问题进行初始化，并确定参考变量，即参考 车辆速度、发动机和电磁能量（或等效力）轨迹，同时确 定档位轨迹。然后，可在单一时域内执行以下顺序程序。
1) 通过线性规划（LP）或二次凸规划（QP）求解最优 控制问题。
2) 基于LP或QP的解更新连续参考变量，即 连续状态和控制变量。
3) 求解换挡优化子问题以获得新 的参考离散控制变量，即挡位轨迹。
4) 若已收敛则停止； 否则返回步骤1。

、γˆm(s)、vˆ(s)和ˆsoc(s)作为请求 发送到下一层，变量上方的（上帽符号）表示该变量是进行线性化的参 考值。若两条连续状态轨迹之间的差异小于某一阈值，则认为已收敛)

算法1和图6解释了上述各个阶段。在算法1中，变量 上方的（ˆ）表示其为参考值，即它来自序列规划中的前 一序列，或由初始参考生成，线性化操作围绕该参考值进 行。问题的初始化在附录A中说明。
LP和QP无法处理混合整数问题。因此，本文通过求 解一个启发式优化子问题并进行顺序迭代以达到收敛，来 寻找次优离散变量，即挡位。换挡优化子问题通过最小化 给定部件（即内燃机或电动机）的力和转速下的能耗，瞬 时找到最佳挡位 $\gamma(s_i)$；然后，从零位置开始，如果满足 以下三个条件，则将$\gamma(s_{i-1})$更新为 $\gamma(s_i)$：1）距离最近一 次换挡已过去某一时间 $\Delta t$；2）燃油节约高于某一阈值；
3） $\gamma(s_{i-1})$不再可行。上述三个条件可防止频繁换挡。
对于内燃机，给定位置$s_i$下的 $\gamma_e(s_i)$按如下方式确定。
Find $\gamma_e(s_i) \in [0,…, 12]$
to minimize $F_f(\gamma_e(s))$ (19a)
subject to
$$
0 \leq \frac{R_w}{r_e(\gamma_e(s))} \hat{F} e(s) \leq T {le} \left( \frac{r_e(\gamma_e(s))}{R_w} \hat{v}(s) \right) \quad (19b) \
\omega_{emin} \leq \frac{r_e(\gamma_e(s))}{R_w} \hat{v}(s) \leq \omega_{emax}. \quad (19c)
$$
允许进行多步换挡，例如从空挡0换到最高档12，或 反之。 $T_{el}$、 $\omega_{emin}$和 $\omega_{emax}$表示根据图4确定的发动机最 大扭矩和转速限制。优化问题(19)的成本函数和约束为非 线性。然而，由于可行换挡次数较少，可在预测范围内快 速求解。类似的优化问题也可用于电动机换挡选择，但在 本论文中，假设 $\gamma_m(s) = \hat{\gamma}_m(s)$为固定值。初始参考生 成在附录A中描述。

C. 序贯线性规划

为了推导出线性最优控制问题，成本函数 $L$ 以及
约束 $f$ 和 $g$ 需要相对于控制变量和连续状态 $z(s)=$
$[F_e(s), F_{mw}(s), F_{br}(s), F_{del}(s), v(s), soc(s), t(s)]$ 在参考值 $\hat{z}(s)$ 附近对控制变量和连续状态进行线性化处理。
$$
L_{lin}(z, s) = L(\hat{z}, s) + \nabla^T L(\hat{z}, s)[z - \hat{z}], \quad (20)
$$
$$
f_{lin,i}(z, s) = f_i(\hat{z}, s) + \nabla^T f_i(\hat{z}, s)[z - \hat{z}], \quad i = 1,…, 3, \quad (21) \
g_{lin,j}(z, s) = g_j(\hat{z}, s) + \nabla^T g_j(\hat{z}, s)[z - \hat{z}], \quad j = 1,…, 12, \quad (22)
$$
其中 $\nabla = \frac{d}{dz}$是梯度算子。为提高可读性，从 $z(s)$中省略 了函数参数。值得注意的是，线性规划和二次规划离散变 量是固定的，即 $\gamma_e(s) = \hat{\gamma} e(s)$ 和 $\gamma_m(s) = \hat{\gamma}_m(s)$。这些参 考轨迹的初始值的获取方法见附录A。新增的控制变量 $F {del}(s)$如下所述。
值得注意的是，优化问题(18)的成本函数和约束并非 所有项都相对于所有状态和控制变量为非线性。此外，由 公式(16k)给出的涉及 $F_{mc}$的项对于正负 $F_{mw}$具有两种 不同的函数描述，这对于准确建模电损耗是必要的。可以 为电力推进部件推导出线性损耗模型。利用公式 (16l)‐(16n)，可以证明
$$
F_{del}(s) = F_{mc}(s) - F_{mw}(s) + F_{db}(s) = F_{mc}(s) - F_{mw}(s) + \frac{Rv(s)}{V_b^2} (F_{mc}(s) + F_a(s))^2. \quad (23)
$$
此外，通过将公式(16o)中的 $F_m(s)$代入公式(16k)，可得
$$
F_{mc}(s) =
\begin{cases}
\frac{1}{v(s)} \sum_{i=0}^{5} \sum_{j=0}^{5} \left( h^+ {ij} \left( \frac{r_m(\hat{\gamma}_m(s))}{R_w} v(s) \right)^i \left( \frac{R_w F {mw}(s)}{r_m(\hat{\gamma} m(s)) \eta {tm}} \right)^j \right), & F_m(s) > 0 \
\frac{1}{v(s)} \sum_{i=0}^{5} \sum_{j=0}^{5} \left( h^- {ij} \left( \frac{r_m(\hat{\gamma}_m(s))}{R_w} v(s) \right)^i \left( \frac{R_w F {mw}(s) \eta_{tm}}{r_m(\hat{\gamma} m(s))} \right)^j \right), & F_m(s) \leq 0.
\end{cases} \quad (24)
$$
因此， $F {del}$ 是 $F_{mw}(s)$ 和 $v(s)$ 的一个显性非线性函 数，可通过一阶泰勒展开进行线性化，如下所示。
$$
F_{lin,del}(F_{mw}(s), v(s), s) = F_{del}(\hat{F} {mw}(s), \hat{v}(s), s) + \frac{\partial F {del}(\cdot)}{\partial F_{mw}} \bigg| {(\hat{F} {mw}(s),\hat{v}(s))} (F_{mw}(s) - \hat{F} {mw}(s)) + \quad (25) \
\frac{\partial F {del}(\cdot)}{\partial v} \bigg| {(\hat{F} {mw}(s),\hat{v}(s))} (v(s) - \hat{v}(s)),
$$
其中，$\hat{F} {mw}(s)$ 和 $\hat{v}(s)$ 是在先前的SLP序列中确定的参考值。
式(25)是 $F {mw}(s)$的分段线性函数，包含两段，分别对 应 $F_{mw}(s)$的正值和负值。为了在线性规划中处理此项， 本文对该等式约束进行了松弛，并引入 $F_{del}$作为新的控 制或优化设计变量，使得
$$
g_{13}: F_{lin,del}(F_{mw}(s), v(s), s) - F_{del}(s) \leq 0. \quad (26)
$$
然而，上述松弛通过在目标函数中引入 $F_{del}$扩大了 可行集；因此，我们确保最优解是紧的，即它不会位于扩 大的可行域内。这意味着在最优解处，式(25)或式(24)中 的某一个分段将取等号。直观上，紧性得以保证，因为该 松弛会导致产生更高的损耗，而优化器会最小化这些损耗。
因此，优化器会使该松弛变为紧的。关于最优解紧性的进 一步讨论可参见[29]和[30]。
此外，在成本函数中，由公式(17)给出的等效发动机 燃油力 $F_f$是 $F_e(s)$和$v(s)$的显函数，可通过一阶泰勒展开 进行线性化（即仿射近似）。
$$
F_{lin,f}(F_e(s), v(s), s) = F_f(\hat{F} e(s), \hat{v}(s), s) + \frac{\partial F_f(\cdot)}{\partial F_e} \bigg| {(\hat{F} e(s),\hat{v}(s))} (F_e(s) - \hat{F}_e(s)) + \frac{\partial F_f(\cdot)}{\partial v} \bigg| {(\hat{F} e(s),\hat{v}(s))} (v(s) - \hat{v}(s)). \quad (27)
$$
因此，线性成本函数如下所示。
$$
J {lin} = \int_{s_0}^{s_f} (F_{lin,f}(F_e(s), v(s), s) + F_{br}(s) + F_{del}(s))ds. \quad (28)
$$
此外，作为控制变量引入的 $F_{del}(s)$，通过式(23)对约 束 $f_2$进行线性化，并改变了约束 $g_7$和 $g_8$。
$$
f_2: \frac{dsoc(s)}{ds} = -\frac{1}{E_{bmax}} (F_{mw}(s) + F_{del}(s) + F_a(s)) \quad (29) \
g_7: p_{bmin} - v(s)(F_{mw}(s) + F_{del}(s) + F_a(s)) \leq 0 \quad (30) \
g_8: v(s)(F_{mw}(s) + F_{del}(s) + F_a(s)) - p_{bmax} \leq 0. \quad (31)
$$
此外，应定义更多约束以确定线性化的信赖域。信赖域 是一个区域
在参考点附近，该近似在一定程度上仍接近原始的非线性函 数。
$$
g_{14}: \hat{v}(s) - \rho_v - v(s) \leq 0 \quad (32) \
g_{15}: v(s) - \hat{v}(s) - \rho_v \leq 0 \quad (33) \
g_{16}: \hat{F} e(s) - \rho_1 \hat{F}_e(s) - \rho_0 - F_e(s) \leq 0 \quad (34) \
g {17}: F_e(s) - \hat{F} e(s) - \rho_1 \hat{F}_e(s) - \rho_0 \leq 0 \quad (35) \
g {18}: \hat{F} {mw}(s) - \rho_1 \hat{F} {mw}(s) - \rho_0 - F_{mw}(s) \leq 0 \quad (36) \
g_{19}: F_{mw}(s) - \hat{F} {mw}(s) - \rho_1 \hat{F} {mw}(s) - \rho_0 \leq 0, \quad (37)
$$
其中 $\rho_v$、 $\rho_1$和 $\rho_0$定义了信赖域的边界，这些边界直接影 响序列规划的收敛速率。 $F_{br}(s)$、 $F_{del}(s)$、$soc(s)$和 $t(s)$的 信赖域包含其整个可行范围。常数$\rho_0$用于确保当 $F_e(s)$和 $F_{mw}(s)$为零时， $F_e(s)$和 $F_{mw}(s)$不会被固定为零。

D. 具有更新成本函数的序列凸二次规划

在凸二次规划（QP）中，成本函数是凸二次的，而 约束条件在状态和控制变量中是线性的。因此，线性规划 （LP）与二次规划（QP）之间的唯一区别在于，在二次 规划中，成本函数（28）应为凸二次函数而非线性函数。
成本函数中唯一的非线性项是由公式(17)给出的 $F_f$，该
项必须通过二次函数 $F_{sqp,f}$进行近似
$$
F_{sqp,f}(F_e(s), v(s), s) = F_f(\hat{F} e(s), \hat{v}(s), s) + \frac{\partial F_f(\cdot)}{\partial F_e} \bigg| {(\hat{F} e(s),\hat{v}(s))} (F_e(s) - \hat{F}_e(s)) + \frac{\partial F_f(\cdot)}{\partial v} \bigg| {(\hat{F} e(s),\hat{v}(s))} (v(s) - \hat{v}(s)) + \quad (38) \
\frac{1}{2} \left[ \frac{\partial^2 F_f(\cdot)}{\partial F_e^2} \bigg| {(\hat{F} e(s),\hat{v}(s))} (F_e(s) - \hat{F}_e(s))^2 + 2 \frac{\partial^2 F_f(\cdot)}{\partial F_e \partial v} \bigg| {(\hat{F} e(s),\hat{v}(s))} (F_e(s) - \hat{F}_e(s))(v(s) - \hat{v}(s)) + \frac{\partial^2 F_f(\cdot)}{\partial v^2} \bigg| {(\hat{F} e(s),\hat{v}(s))} (v(s) - \hat{v}(s))^2 \right].
$$
然而，公式(38)中的二次近似并不总是对所有 $s$的值 都是凸的，因为得到的Hessian矩阵$H(s)$并非始终是对称 且半正定的。该Hessian矩阵可通过重新整理公式(38)的 各项得到其形式
$$
F {sqp,f}(\cdot) = [F_e(s), v(s)]^T H(s)[F_e(s), v(s)] + f^T(s)[F_e(s), v(s)]. \quad (39)
$$
在本论文中，通过提取Hessian矩阵的半正定部分来 确保二次近似的凸性，从而
$$
F_{sqp,f}(\cdot) = [F_e(s), v(s)]^T H_{psd}(s)[F_e(s), v(s)] + f^T(s)[F_e(s), v(s)], \quad (40)
$$
其中 $H_{psd}(s)$是 $H(s)$的半正定部分。Hessian矩阵 $H(s)$是对称
的，可写成形式 $Q^T D Q$，其中 $D = \text{diag}(\lambda_1, …, \lambda_n)$ 且 $\lambda_i, i = 1…n,$
是Hessian矩阵的特征值。然后，矩阵 $D$可以写成两个矩 阵的和，即 $D = D_{pos} + D_{neg}$，其中 $D_{pos}$和 $D_{neg}$的对 角线上分别仅有正特征值和负特征值。接着，
$$
H_{psd}(s) = Q^T(s)D_{pos}(s)Q(s). \quad (41)
$$
方程(40)在 $F_e(s)$和 $v(s)$上是凸的且为二次函数。因此， 二次成本函数变为
$$
J_{sqp} = \int_{s_0}^{s_f