二分搜索树

最新推荐文章于 2025-08-03 10:00:00 发布

原创最新推荐文章于 2025-08-03 10:00:00 发布 · 130 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二分搜索树

数据结构专栏收录该内容

8 篇文章

订阅专栏

本文深入探讨了二分搜索树的定义与特性，包括其结构、添加元素、查找元素的方法，以及前序、中序、后序遍历的递归与非递归实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二分搜索树：首先，二分搜索树要先是二叉树，其次二叉树的左节点比根节点小，右节点比根节点大。

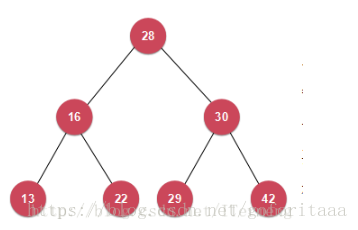此树是一棵完全二叉树

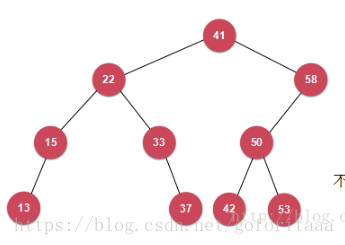也可以不是完全二叉树，只要满足左孩子比根节点小，右孩子比根节点大就行，其他不限制。

以左右孩子为根又是一棵小二叉树。

代码实现：

public class BST <E extends   Comparable <E>> {



   private  class Node{
               public     E e;//数据
               public     Node left;
               public    Node right;

                public Node( E e ){
                      this.e = e;
                      this.right = null;
                      this.left = null;

                  }
//                  @Override
//                  public String toString()
//                  {
//                      return e.toString();
//                  }

                }private  Node root;
               private Node left;
               private Node right;
               private int size;
               //初始化树
            public BST(){
                this.right = null;
                this.root=null;
                this.left = null;
                size = 0;

            }
            //获取树的长度
          public int getSize(){
                return size;
          }
          //判断树是否为空树
         public boolean isEmpty(){
                return size==0;

         }

}

二叉树的添加

首先判断要添加的节点和根节点比较，如果比根节点小，就和根节点的左孩子比较，如果比根节点大，就和右孩子比较。

以此类推，在分别以根节点的左孩子和右孩子为根，在进行比较。

对于二分搜索树的存储

递归方法：先判断终止条件，在判断循环体逻辑

  //向以node为根的二分搜索树中插入元素E,递归算法

private void add(Node node,E e) {

    if (e.equals(node.e))
        return;
    //先判断终止条件
    if (e.compareTo(node.e) < 0 && node.left == null) {
        node.left = new Node(e);
        size++;
        return;
    }
    if (e.compareTo(node.e) > 0 && node.right == null) {
        node.right = new Node(e);
        size++;
        return;
    }
    //循环体逻辑
    if (e.compareTo(node.e) < 0) {
        add(node.left, e);
    } else {
        add(node.right, e);
    }

}

判断该二分搜索树是否包含某元素

public void Conatains(E e){
         Node node = root;
         contains(node,e);

}
//判断以node为根的树，是否包含改元素
 private boolean contains(Node node,E e){
         if(node==null){
             return  false;
         }
        if(e.compareTo(node.e)==0){
            return true;
        }
        if(e.compareTo(node.e)<0){
            return   contains(node.left,e);
        }else{
            return contains(node.right,e);
        }

 }

二分搜索树的遍历

前序遍历

private void printOrder(Node node){
        //递归终止的条件
        if(node==null){
            return ;
        }
        //递归逻辑，没有终止
        System.out.println(node.e);

        printOrder(node.left);
        printOrder(node.right);


}

中序遍历

 public void inOrder(){
        inOrder (root);
    }
//以node为根的中序遍历二叉排序树
        private void inOrder(Node node){
                    if(node==null){
                        return ;
                    }
                    inOrder(node.left);
                    System.out.println(node.e);
                    inOrder(node.right);
        }

后序遍历

public void postOrder(){
     houOrder(root);

}

private void  houOrder(  Node node){
     if(node==null){
         return ;
     }
     houOrder(node.left);
     houOrder(node.right);
     System.out.println(node.e);

}

前序非递归遍历

采用栈存储，先将根压入栈，因为前序遍历先遍历左孩子，在遍历右孩子，所以先将右孩子入栈在将左孩子入栈。

public void printOrderNR( ){

    Stack<Node>  stack = new Stack<Node>();
         Node e = root;

          stack.push(root);
          while(!stack.isEmpty()) {
              Node cur = stack.pop();
              System.out.println(cur.e);

              if (cur.right != null) {
                  stack.push(cur.right);
              }
              if (cur.left != null) {
                  stack.push(cur.left);
              }
          }
}

非递归层序遍历

采用队列实现，先将根入队，根出队，左孩子入栈，右孩子入队。出队，左孩子入队，右孩子入队，以此类推。

public void levelOrder(){
   Queue<Node> q = new LinkedList<>();
   q.add(root);
   while(!q.isEmpty()){
         Node  cur = q.remove();
         System.out.println(cur.e);
         if(cur.left!=null){
             q.add(cur.left);
         }
         if(cur.right!=null){
              q.add(cur.right);
         }

   }

}