hash基础知识

今天，我们来讲解一下关于hash的概念进行了解。为后面打基础。

解释

首先，大家可能疑惑的是为什么C++中没有hash这个函数接口？其实不然，C++中unordered_xxx

实际就是hash。只是由于C++的历史等原因取名上有了差异而已，未来为了方便，我们就直接说hash了。

为什么会又出现了hash这个算法呢？

原因：在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到$log_2 N$，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想。最好的查询是，进行很少的比较次数就能够将元素找到，因此在C++11中，STL又提供了4个unordered系列的关联式容器

即：unordered_map,unordered_set,unordered_multimap,unordered_multiset

unordered_map

介绍

1. unordered_map是存储<key, value>键值对的关联式容器，其允许通过keys快速的索引到与其对应的value。

2. 在unordered_map中，键值通常用于唯一地标识元素，而映射值是一个对象，其内容与此

键关联。键和映射值的类型可能不同。

3. 在内部,unordered_map没有对<key, value>按照任何特定的顺序排序, 为了能在常数范围内找到key所对应的value，unordered_map将相同哈希值的键值对放在相同的桶中。

4. unordered_map容器通过key访问单个元素要比map快，但它通常在遍历元素子集的范围迭代方面效率较低。

5. unordered_maps实现了直接访问操作符(operator[])，它允许使用key作为参数直接访问value

6.它的迭代器至少是向前迭代器。

接口认识

构造

unordered_map构造（这里是C++11更新的，可先略过，后面讲解C++11时有相关的补充）

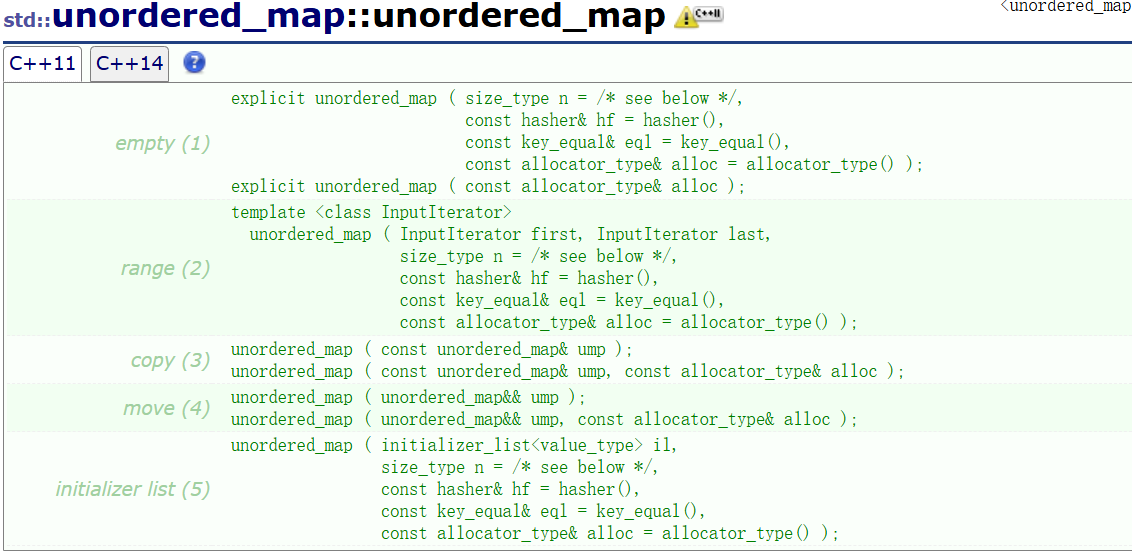
构建unordered_map
构造一个unordered_map容器对象，根据使用的构造函数版本初始化其内容：
(1)空容器构造函数（默认构造函数）
构造一个空的unordered_map对象，不包含任何元素，大小为0。
它可以使用特定的哈希器、key_equal和allocator对象以及最小数量的哈希桶来构造容器。
(2) range构造函数构造一个unordered_map对象，其中包含[first，last)范围内每个元素的副本。

(3)复制构造函数（和带分配器的复制）
该对象被初始化为具有与ump unordered_map对象相同的内容和属性。
(4)移动构造函数（并随分配器移动）该对象获取左值ump的内容。
(5)初始化器列表用列表的内容初始化容器。

Capacity

empty：

检测unordered_map是否为空

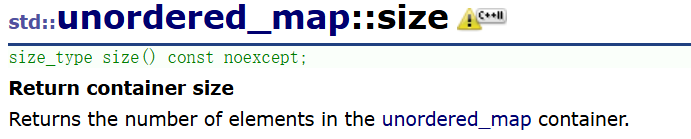
size:

获取unordered_map的有效元素个数

 Element lookup:查找元素

find:

返回key在哈希桶中的位置

在容器中搜索以k为键的元素，如果找到则返回一个迭代器，否则返回一个迭代器给unordered_map::end（超过容器末尾的元素）。
另一个成员函数unordered_map::count仅用于检查特定键是否存在。
映射的值也可以通过使用成员函数at或operator[]直接访问。

count:

返回哈希桶中关键码为key的键值对的个数

对具有特定键的元素进行计数
在容器中搜索键为k的元素，并返回找到的元素个数。因为unordered_map容器不允许重复键，这意味着如果容器中存在具有该键的元素，该函数实际上返回1，否则返回0。 

注意：unordered_map中key是不能重复的，因此count函数的返回值最大为1

Modifiers

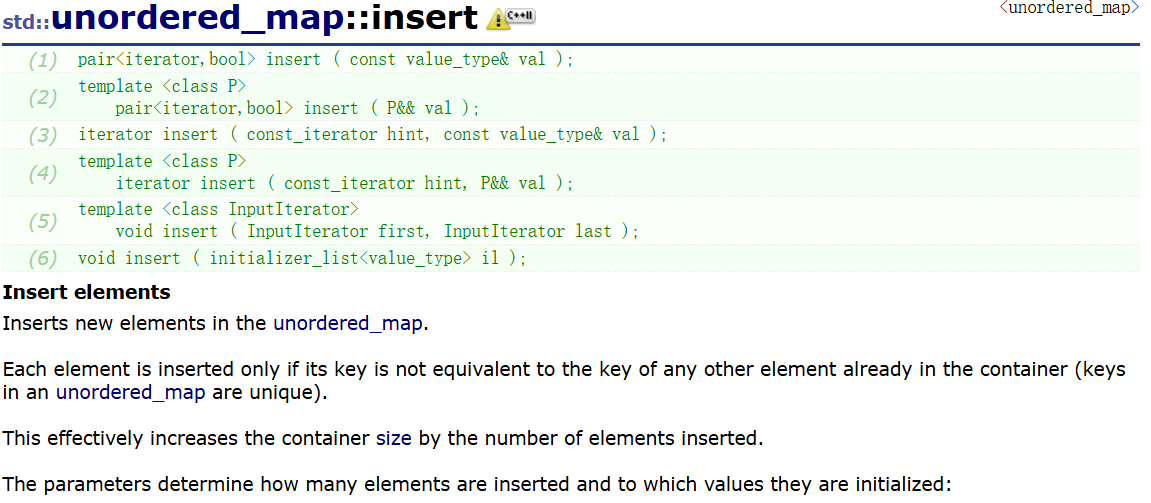
insert

insert元素在unordered_map中插入新元素。
只有当每个元素的键与容器中已有的任何其他元素的键不相等时（unordered_map中的键是唯一的），才会插入该元素。
这有效地通过插入的元素数量增加了容器的大小。
形参决定插入多少个元素以及将元素初始化为哪些值：

erase:

删除容器中的键值对

消除元素
从unordered_map容器中删除单个元素或一系列元素（[first,last）)。
这通过调用每个元素的析构函数，有效地减少了容器的大小。

clear:

清空容器中有效元素个数

unordered_map容器中的所有元素都被删除：调用它们的析构函数，并将它们从容器中删除，使容器的大小为0。

 

swap:

交换两个容器中的元素

交换内容
用ump的内容交换容器的内容，ump是另一个包含相同类型元素的unordered_map对象。大小可能不同。
在调用这个成员函数之后，这个容器中的元素是调用之前在ump中的元素，而ump的元素是在this中的元素。容器内部保存的其他对象（例如它们的hasheror key_equal对象）也被交换。
该函数在容器之间交换指向数据的内部指针，而不实际对单个元素执行任何复制或移动 

Buckets桶操作

（ps:现在看不懂的话可先跳过，后面会讲到）

 

返回哈希桶中桶的总个数

返回unordered_map容器中的桶数。
bucket是容器内部哈希表中的一个槽，根据键的哈希值将元素分配给该槽。
桶的数量直接影响容器哈希表的负载因子（从而影响碰撞的概率）。容器自动增加桶的数量以保持负载因子低于特定阈值（其max_load_factor），每次需要增加桶的数量时都会导致重新散列。

返回n号桶中有效元素的总个数

返回桶n中元素的个数。
bucket是容器内部哈希表中的一个槽，根据键的哈希值将元素分配给该槽。
存储桶中元素的数量影响访问存储桶中特定元素所需的时间。容器会自动增加桶的数量，以保持负载因子（桶的平均大小）低于max_load_factor。

返回键为k的元素所在的桶号。
bucket是容器内部哈希表中的一个槽，根据键的哈希值将元素分配给该槽。桶的编号从0到（bucket_count-1）。
bucket中的单个元素可以通过unordered_map::begin和unordered_map::end返回的范围迭代器来访问。

跟之前一样，这里只弄出了常见的，其他的可以自己自行去官网那里查。

另外，unordered_set，unordered_multiset,unordered_multimap的接口也是差不多的，相信大家都学习到了hash部分，都是能自行看懂的。

好了，有了上面的铺垫，现在。我们正式来hash的概念：

hash概念：

前序：

实际上：顺序结构（比如类似数组那样单独结构）以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O($log_2 N$)，搜索的效率取决于搜索过程中元素的比较次数。

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素

举个生活中的例子：如图书馆中找书，它可能会根据书名的编号，开头字母等等来减少直接去寻找的麻烦，那么，当我们直接按照的书本编号，字母去对应的区域去找，这是不是就极大提高了我们的效率了。

因此，有了上面等等例子，我们就可以代入到下面的情况：

插入元素

根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放

搜索元素

对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功

上述的方法就叫做：哈希（散列）：存储的值跟存储位置建立出一个对应的关系。

哈希函数的分类：

直接定址法：

而上面我们举例图书馆找书的方法又叫做：直接定址法（也是我们常用的方法）。

改进：当我们的数据集中分布在100-110之间2，难道我们就肆意去开110以上的空间吗？其实不必这样，我们可以使用之前了解过的计数排序的思路：；去映射到1-10对应的位置即可了。Hash（Key）= A*Key + B

那么，我们再来谈谈，直接定址法什么情况都可以适用吗？其实不然，它只适用于字母开头分类的特点：范围集中（小），而如果我们的数据很分散，就不适用直接定址法了。

优点：简单、均匀

缺点：需要事先知道关键字的分布情况

使用场景：适合查找比较小且连续的情况

除留余数法：

概念：设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：Hashi（下标位置) = key% n(n<=m),将关键码转换成哈希地址

它是针对于直接定址法的不足：；是使用于值的分布范围分散。

比如说：有{27，47，67，15}使用除留余数法就是下图：

但是，这里就又会出现问题：

1.由Hashi（下标位置) = key% n(n<=m)算出来的是一个整形，那么字符串呢？

解决方案：再弄一个映射。（后面我们模拟实现代码中就会明白这思路了）

2.不同的值（如47），可能会映射到同一个位置，值和位置是多对一的关系了，这种问题我们称为哈希冲突/碰撞 

哈希冲突：

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。

因此，我们的哈希函数设计原则：

1.哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须在0到m-1之间

2.哈希函数计算出来的地址能均匀分布在整个空间中

3.哈希函数应该比较简单

面对哈希冲突了，我们该怎么去应对呢？

这里的话结合着代码来看更加容易理解，所以关于它的讲解，我们就放到模拟实现hash表那里去讲解了（也就是下一篇文章）。

另外，我们再进行拓展一下：

关于更多的哈希函数的设计方案有哪些：

3. 平方取中法--(了解)

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；

再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址

平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况

4. 折叠法--(了解)

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。

折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

5. 随机数法--(了解)

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。

通常应用于关键字长度不等时采用此法

6. 数学分析法--(了解)

设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散列地址。例如

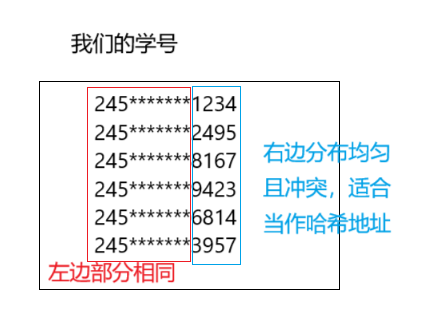
我们的学号前面的数字极有可能都是 相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取还容易出现 冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。

好了，关于哈希的基础铺垫的知识就讲解完了，希望我们一起进步！

最后，到了本次鸡汤环节：

对，祝你快乐！