二叉查找树，平衡二叉树及红黑树详细解析笔记--简明易懂

随身携带的笑

已于 2023-02-04 13:40:18 修改

阅读量536

点赞数 1

CC 4.0 BY-SA版权

分类专栏： # Java基础学习经验文章标签：数据结构

于 2023-02-04 12:04:48 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/giveupgivedown/article/details/128876993

学习经验同时被 2 个专栏收录

43 篇文章

订阅专栏

17 篇文章

订阅专栏

文章详细介绍了二叉查找树的概念及其弊端，强调了平衡二叉树为解决查找效率问题而引入，特别是介绍了平衡二叉树的旋转机制，包括左旋和右旋。接着，文章深入探讨了红黑树这一自平衡二叉查找树，阐述了红黑树的五条规则以及在添加节点时如何维护平衡，展示了不同情况下调整颜色和旋转的策略，表明红黑树在效率上的优势。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

目录

一.二叉查找树
二.平衡二叉树
- 2.1 旋转机制
三.红黑树

一.二叉查找树

规则：大的存左边，小的存右边，一样的不存

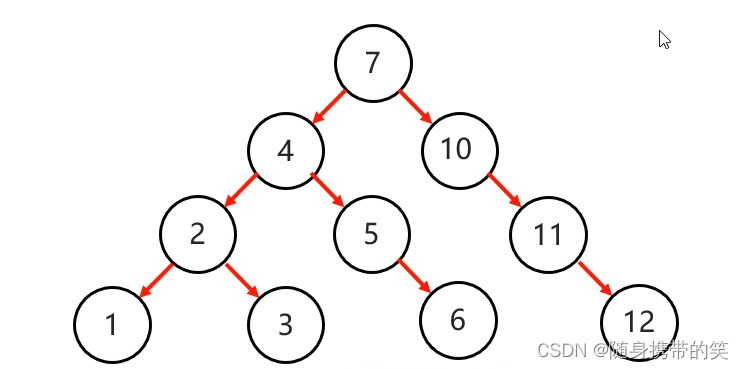
在这里插入图片描述

弊端

但是二叉查找树会导致左右子树高度差过多，查找效率变低，形成链表

如果存入数据有序，结构就会如下图所示，这样查找效率和链表差不多
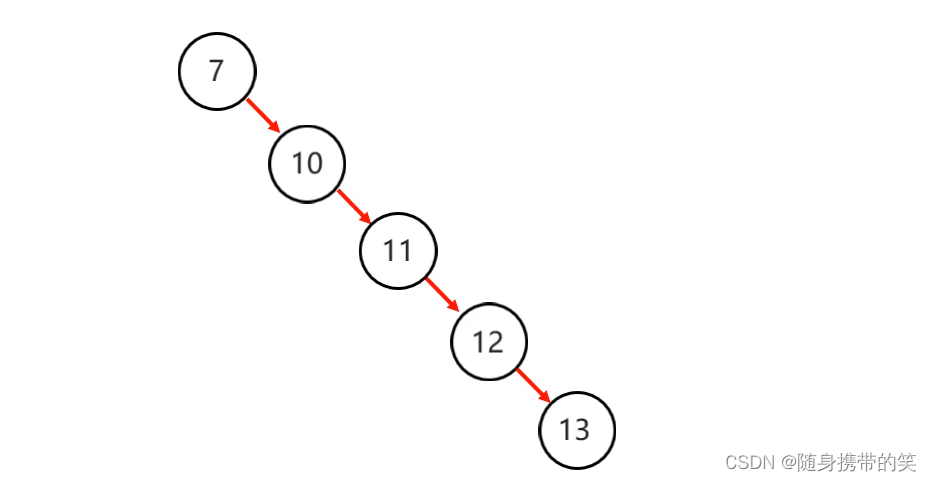
在这里插入图片描述

二.平衡二叉树

平衡二叉树本身也是一棵二叉查找树，只不过在二叉查找树的基础上保证了树的平衡

规则：任意节点左右子树高度差不超过1

弊端：由于添加节点需要判断，旋转，导致添加数据速度慢

下图就不是一个平衡二叉树

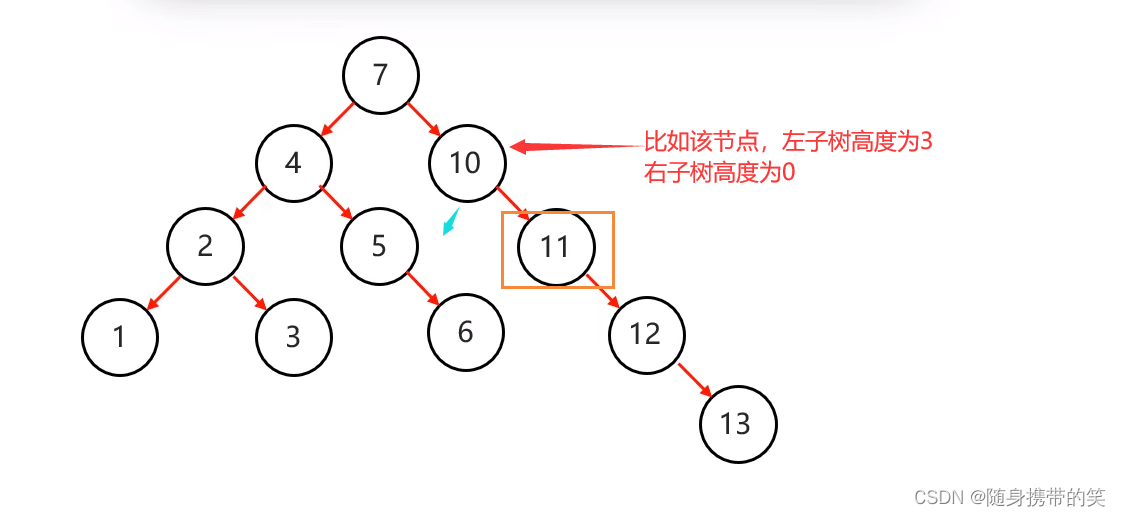
在这里插入图片描述
那么会有一个疑惑，平衡二叉树是如何保持平衡的呢？这就涉及到平衡二叉树的旋转机制了，接下来继续看。

2.1 旋转机制

2.1.1 左旋

首先确定支点，从添加的节点开始，不断往父节点找不平衡的节点，把遇到第一个不平衡的点当作支点去旋转

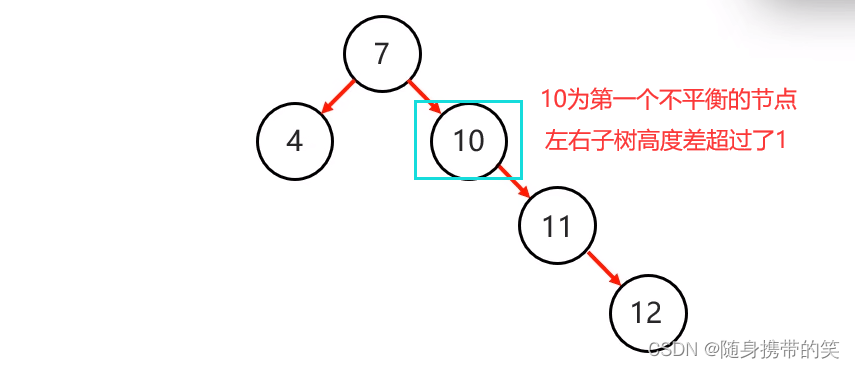
在这里插入图片描述

2.把支点降级，变成左子节点

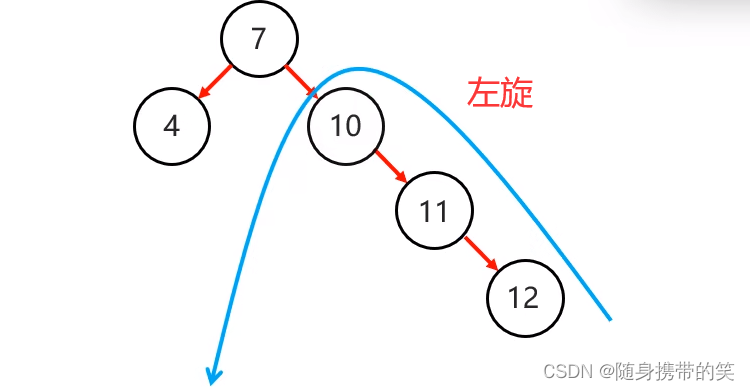
在这里插入图片描述

3.晋升原来的右子节点

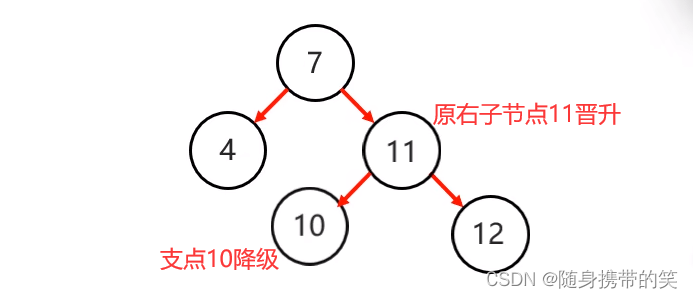
在这里插入图片描述

上面的是一种简单情况，只是为了讲解原理，下面来看常见情景

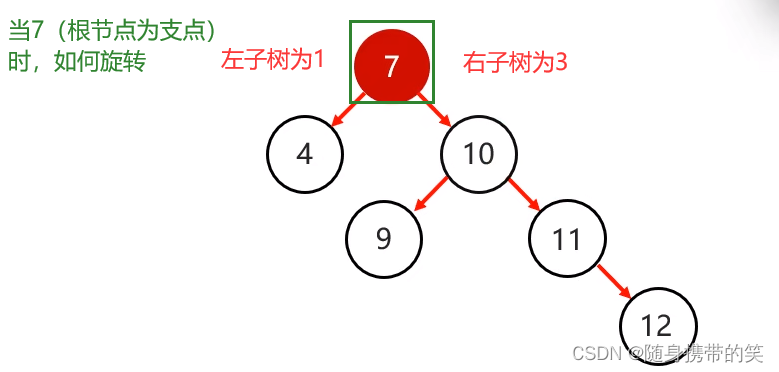
在这里插入图片描述

下面需要将根节点的右侧往左拉，也就是根节点降级

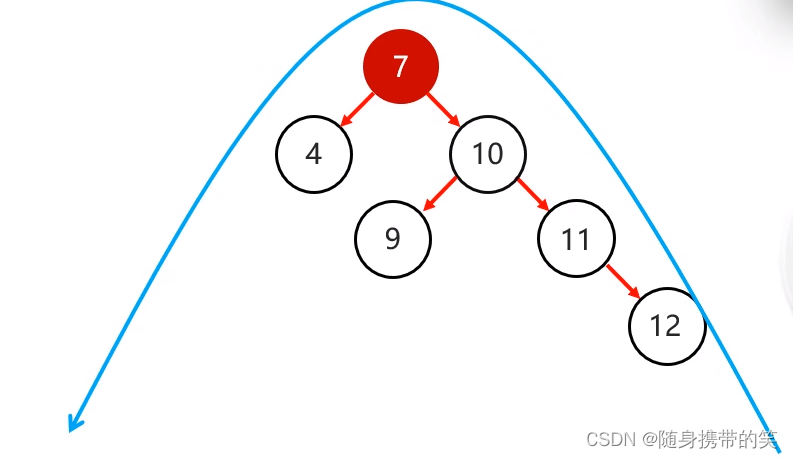
在这里插入图片描述

原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点

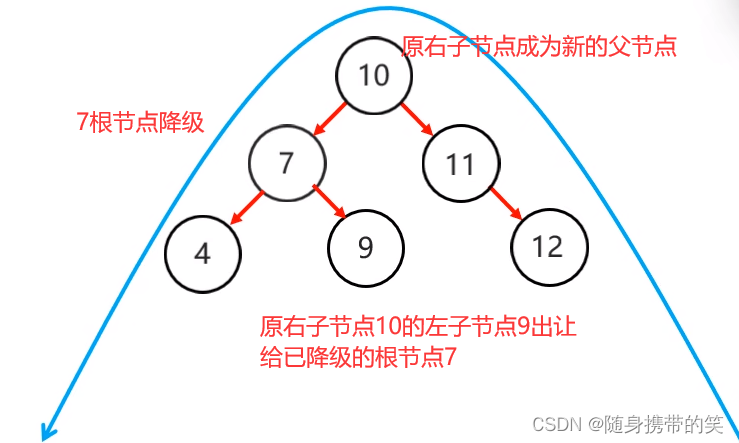
在这里插入图片描述

最后来个左旋动图演示更加清晰明了
在这里插入图片描述

2.1.2 右旋

右旋和左旋道理一样的，就不过多讲解了

1.确定支点:从添加的节点开始，不断的往父节点找不平衡的节点，以不平衡的点作为支点
2.把支点右旋降级，变成右子节点
3.晋升原来的左子节点

动图演示
在这里插入图片描述

2.1.3 触发机制

添加节点时，破坏了树的平衡，就需要旋转

根据插入的位置又分为4种，左左，右右，左右，右左，看不明白很正常，接下来看图解过程

左左

左左:当根节点左子树的左子树有节点插入，导致二叉树不平衡
情形如下图
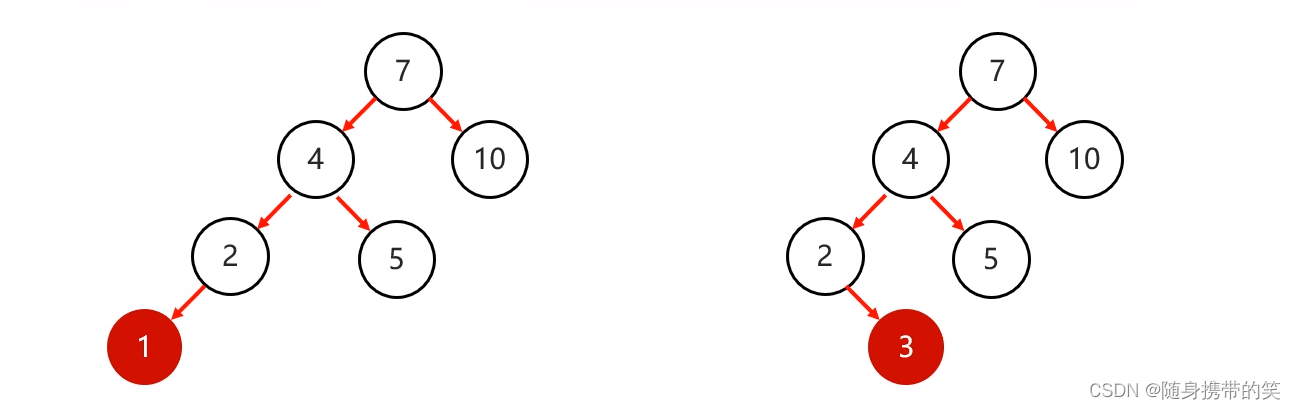
在这里插入图片描述
只需一次右旋解决问题

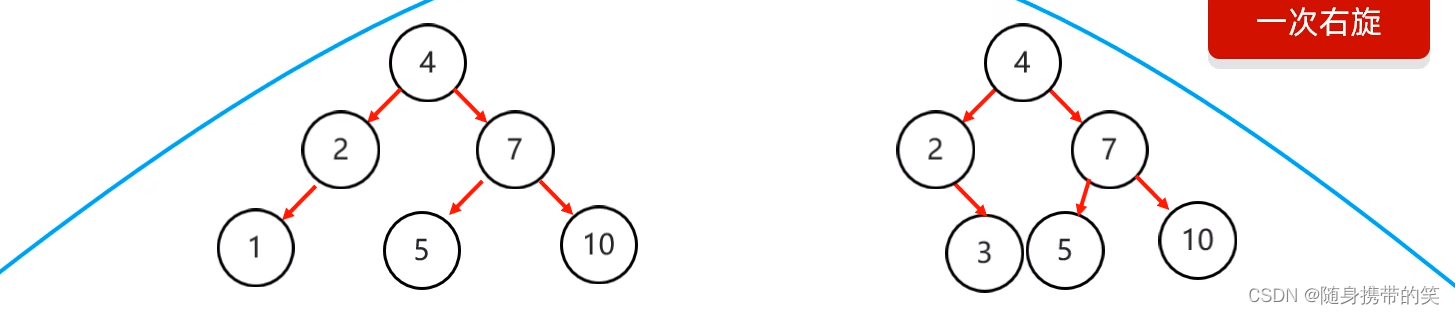
右右

右右:当根节点右子树的右子树有节点插入，导致二叉树不平衡
情形如下图

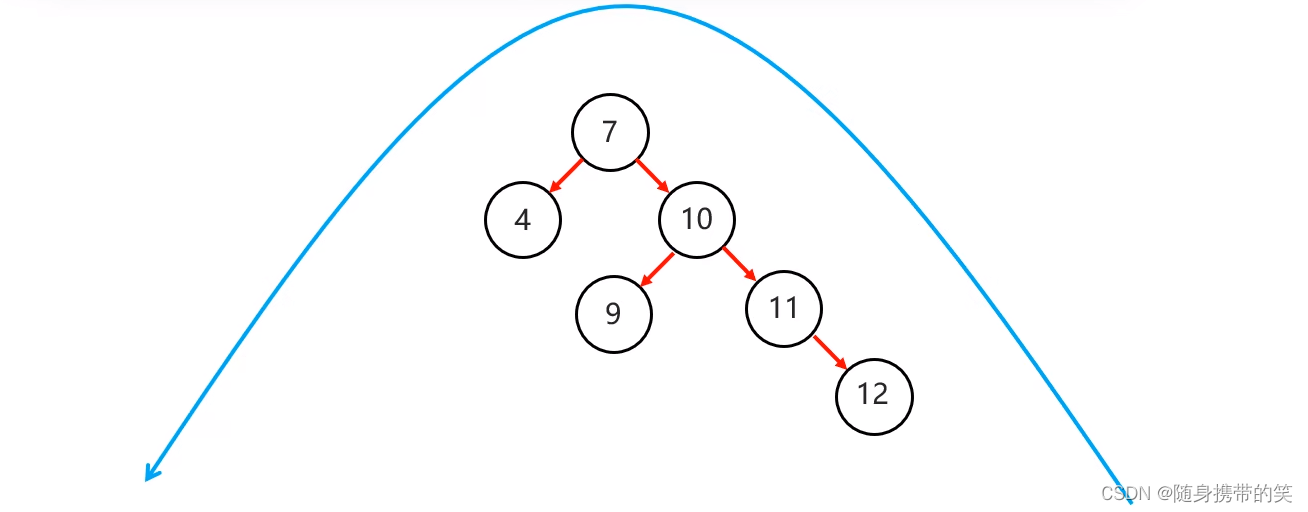
在这里插入图片描述
也只是需要一次左旋就能解决问题

在这里插入图片描述

接下来的两种稍微有点难度，需要两次旋转

左右

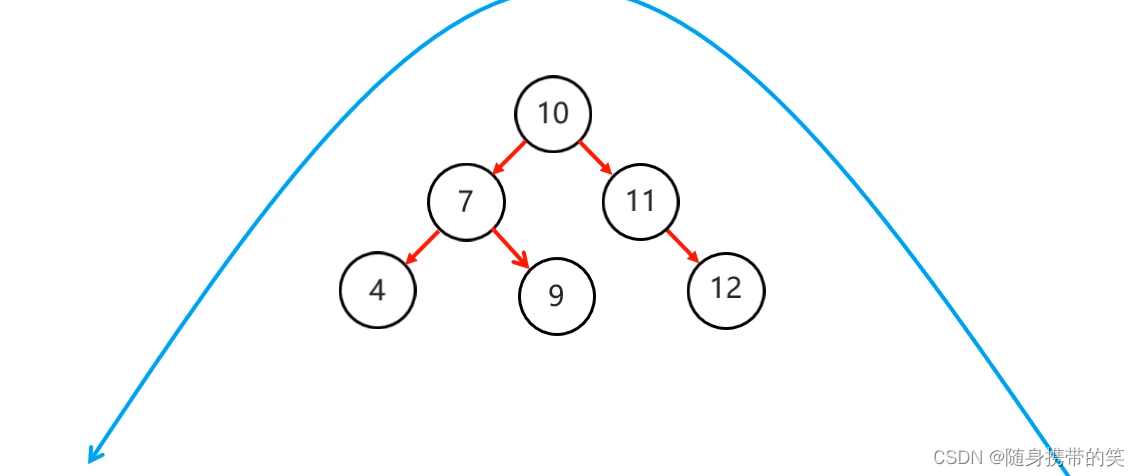
左右:当根节点左子树的右子树有节点插入，导致二叉树不平衡

情形如下图，可以发现一次右旋解决不了问题

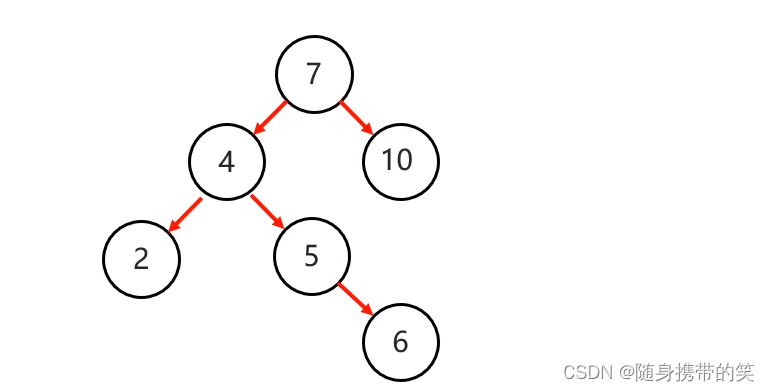
在这里插入图片描述

可以尝试一次，假如一次右旋，结果如何

下面是右旋一次的结果，二叉树仍然没有平衡

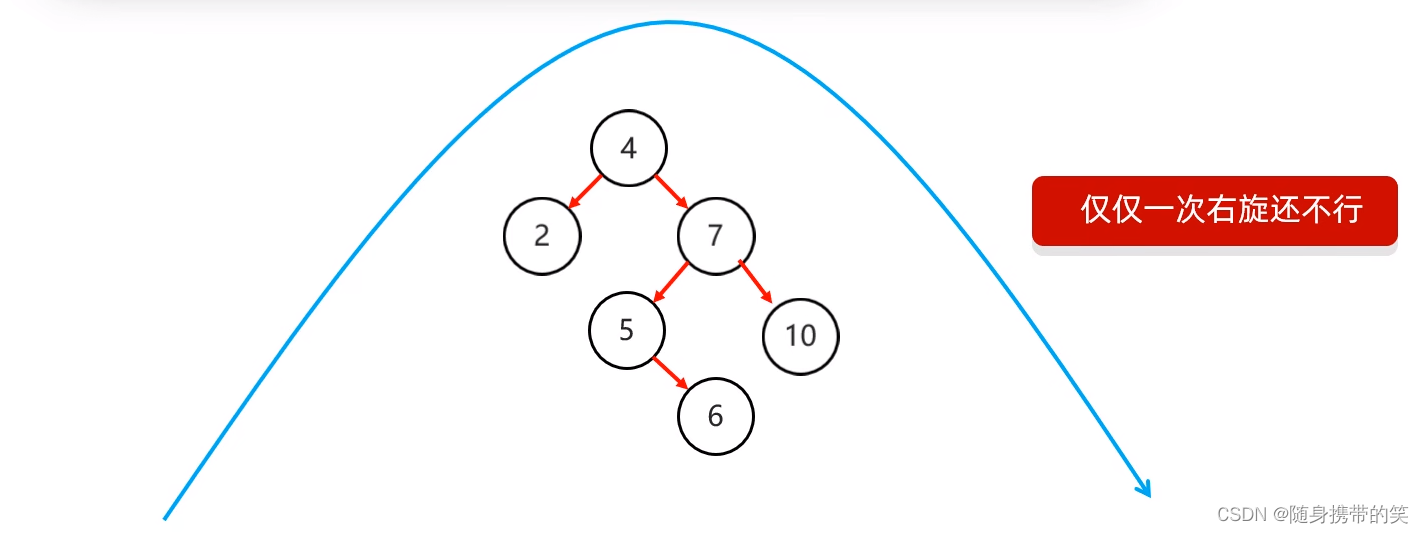
在这里插入图片描述

正确操作如下

原树
在这里插入图片描述

首先局部左旋，将它变成左左，
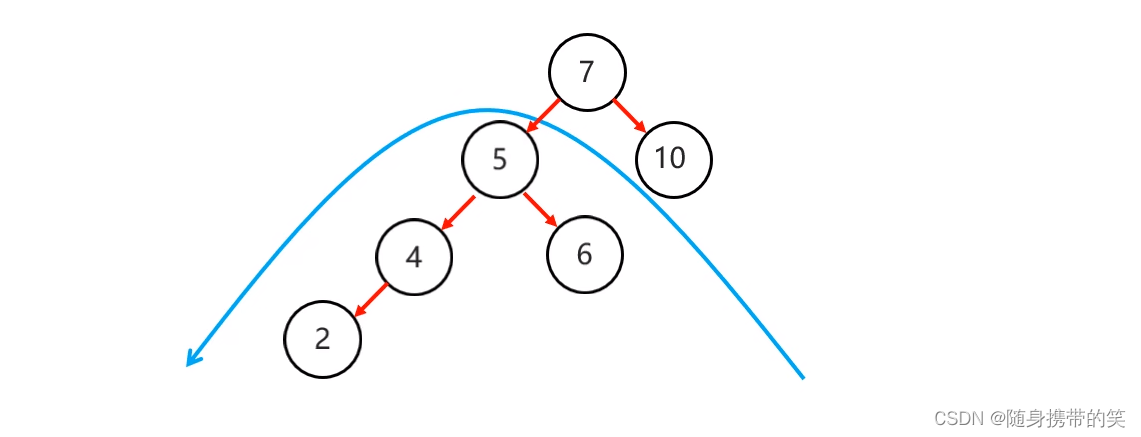
在这里插入图片描述
然后再进行右旋，结果如下

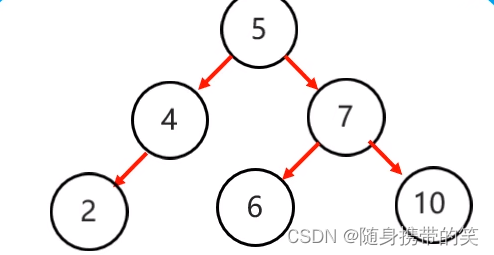
在这里插入图片描述

右左

右左和左右同理

右左:当根节点右子树的左子树有节点插入，导致二叉树不平衡

情形如下图

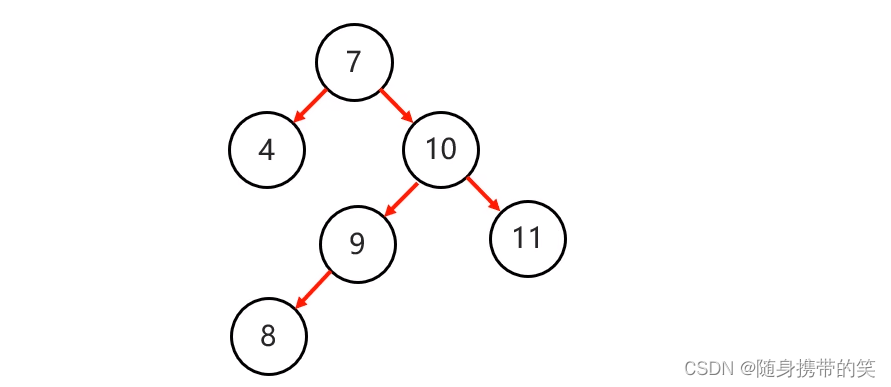
在这里插入图片描述

首先局部右旋，把右左，变为右右

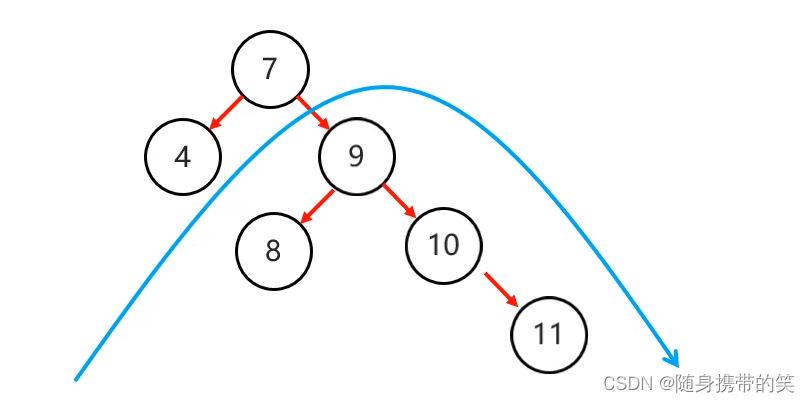
在这里插入图片描述

然后再进行左旋，下面是最终结果

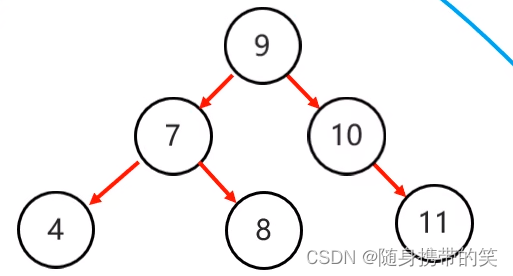
在这里插入图片描述

三.红黑树

红黑树是一种自平衡的二叉查找树

它是一种特殊的二叉查找树，红黑树的每一个节点上都有存储位表示节点的颜色，
每一个节点可以是红或者黑;红黑树不是高度平衡的，它的平衡是通过红黑规则进行实现的

与平衡二叉树的区别
在这里插入图片描述

3.1 红黑规则

①每一个节点或是红色的，或者是黑色的

②根节点必须是黑色

③如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点(Nil)是黑色的

④如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)

⑤对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点;

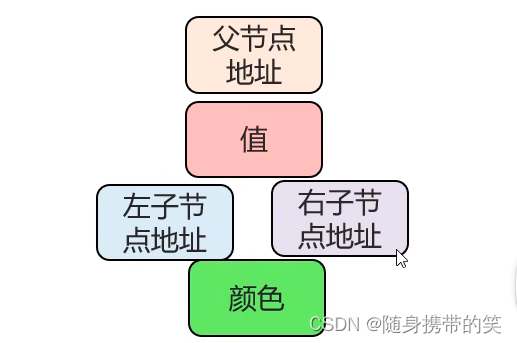
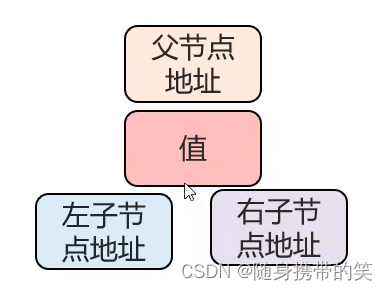
树的节点结构如下

而红黑树的结点结构多了一个颜色

在这里插入图片描述

如下图就不满足红黑规则⑤对每一个节点，从该节点到其所有后代叶节点（就是Nil节点）的简单路径上，均包含相同数目的黑色节点;

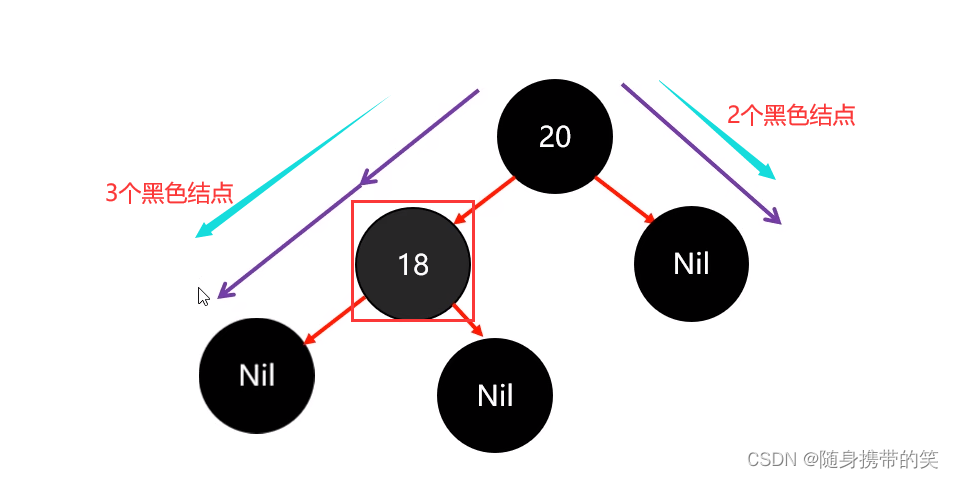
在这里插入图片描述

所以18这个结点应该是红色的

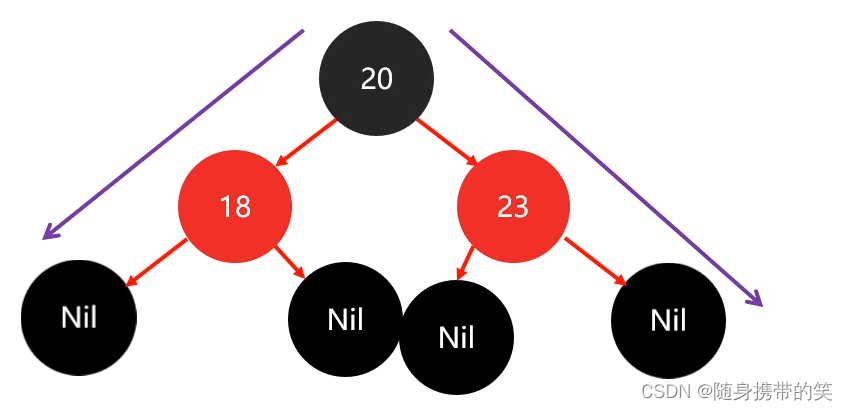
默认颜色：添加节点时默认结点颜色是红色，效率高
还是上图，添加20，18，23；默认黑色的话，18和23 违背原则⑤，都需要调整颜色，调整次数为2
若默认颜色为红，只有20违背原则②根节点必须是黑色，调整次数为1
在这里插入图片描述

3.2 添加节点规则

注意：下面几个例子，都是对照这个规则表来的，看例子对照添加规则表才能看清楚

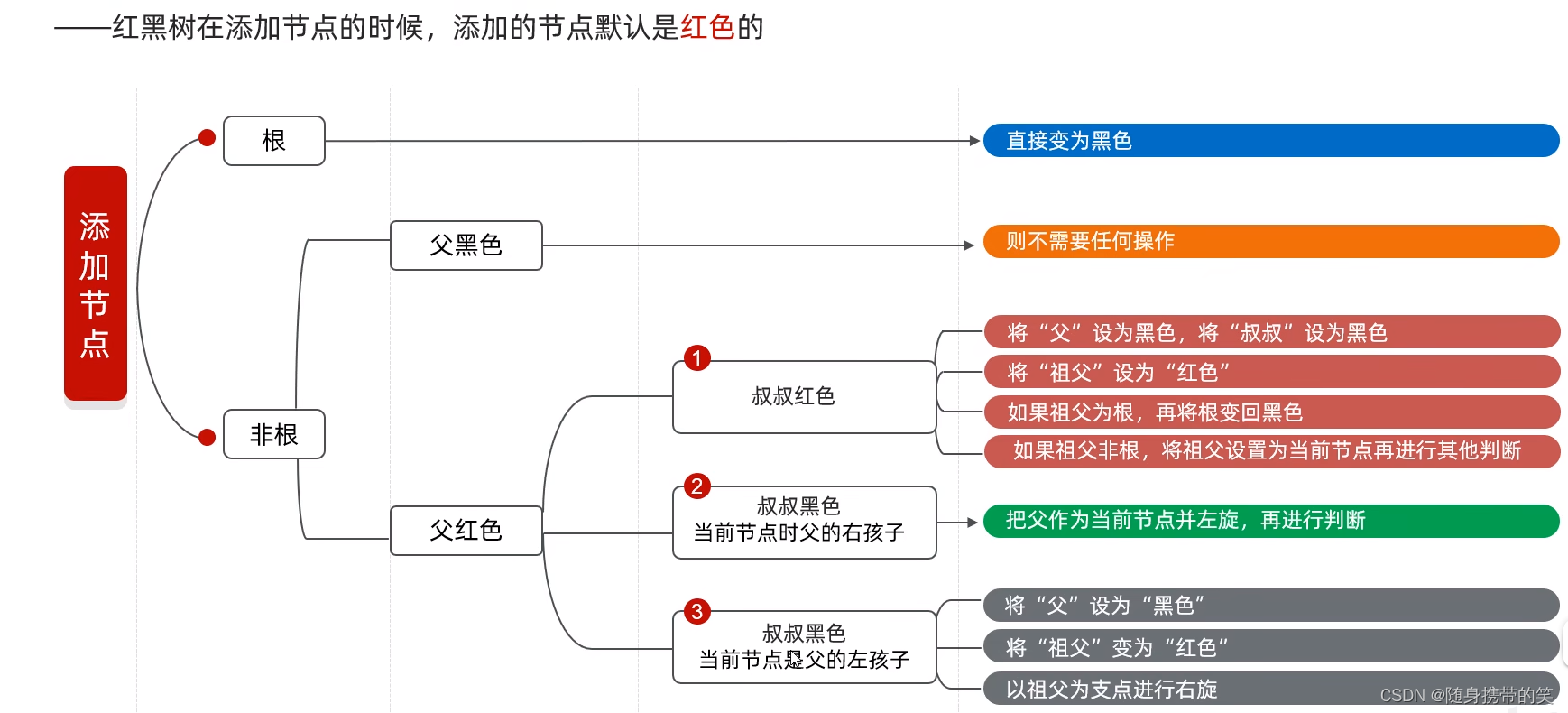
在这里插入图片描述

注：叔叔节点就是跟父节点有同一个爷爷节点

3.2.1 父红色策略①

范例：添加15节点，走上表的父为红，叔叔为红路径①策略

先将父节点设为黑，叔叔节点也设为黑
祖父设为红
祖父非根，以祖父节点再走上面的规则表（就是非根——>父黑色——>不做操作）
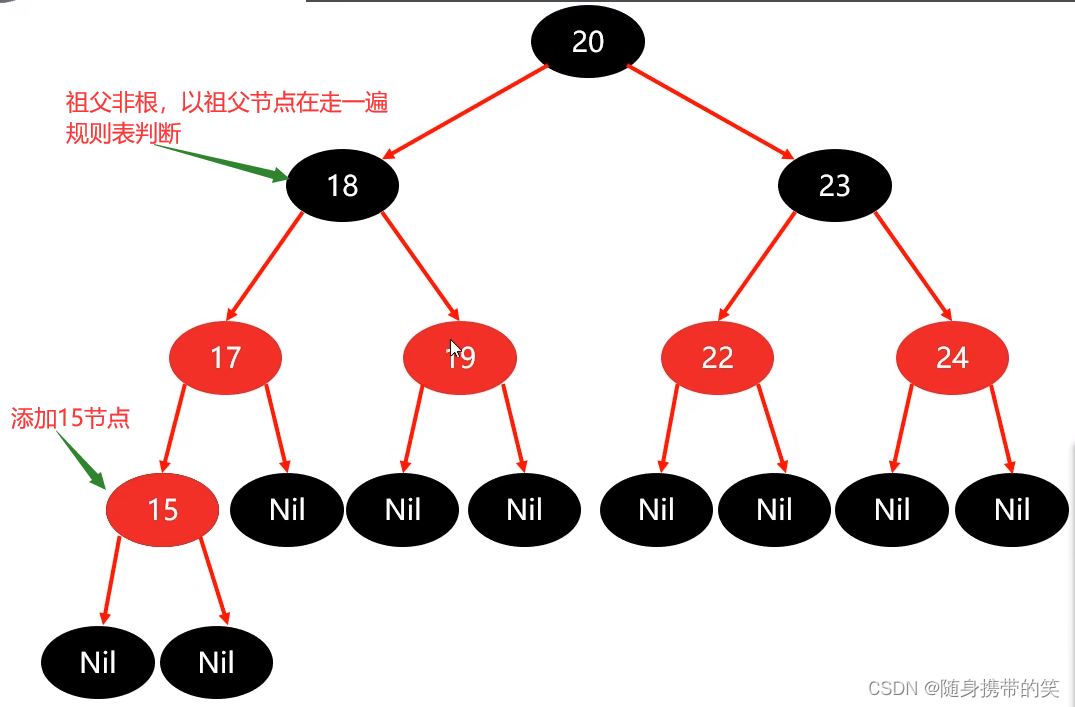
在这里插入图片描述

最后添加完毕结果图如下

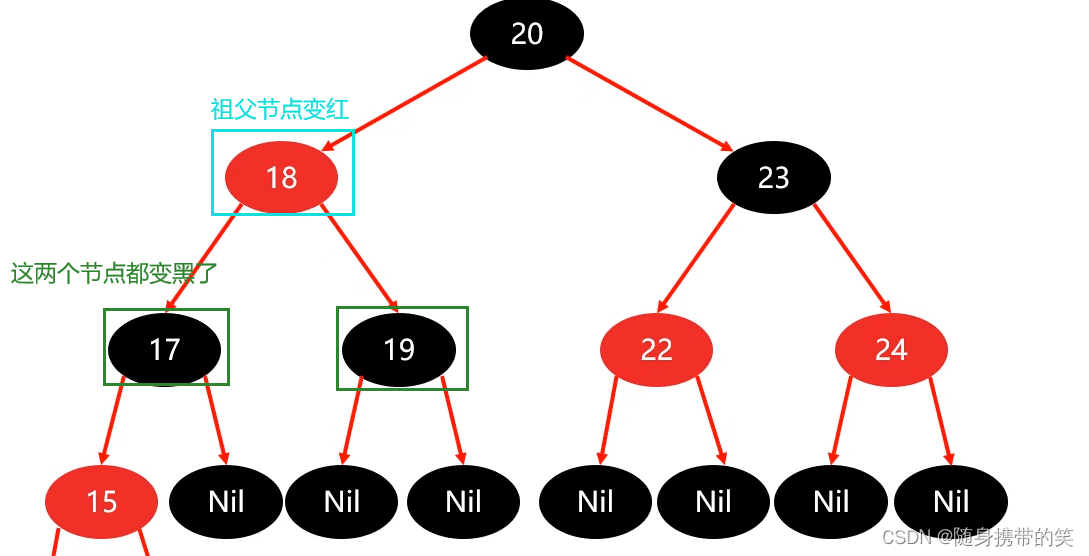
在这里插入图片描述

3.2.2 父红色策略③

下面更难的来了，当添加14节点时的情况又该如何

添加14节点，走规则表的非根——>父红色——>③策略

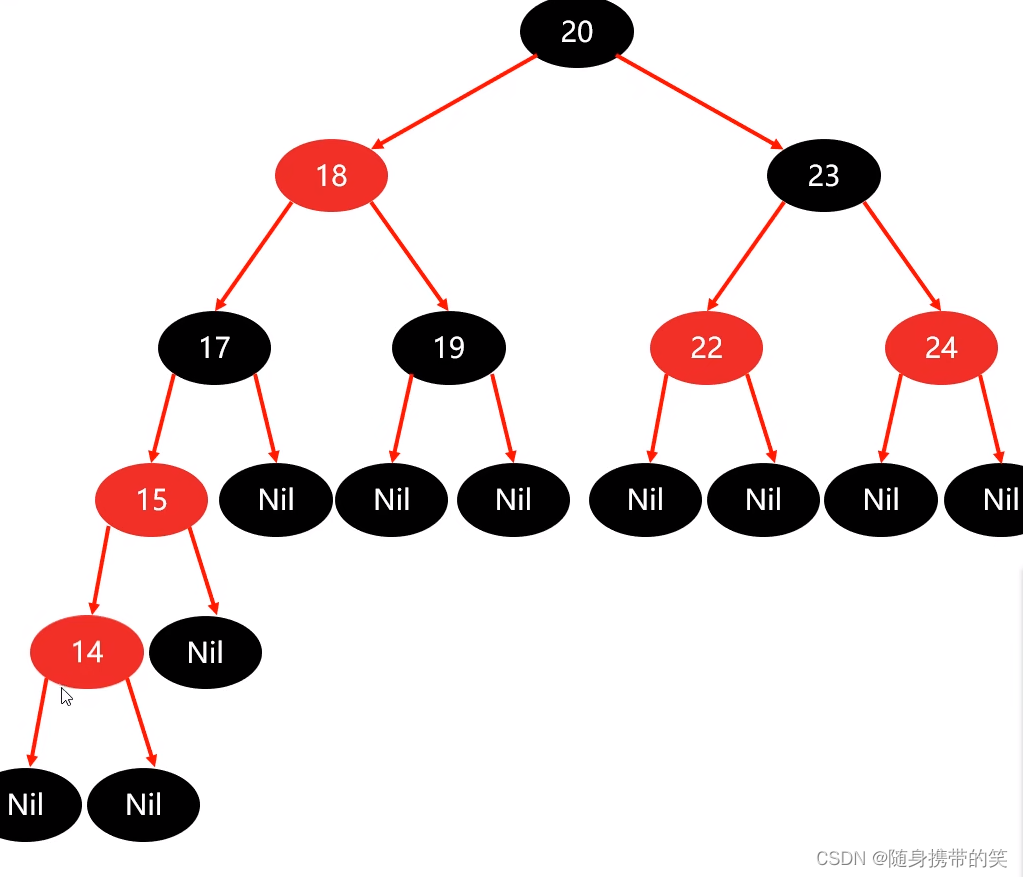
在这里插入图片描述

首先将父节点设为黑色
再将祖父节点设为红色
最后以祖父为支点进行右旋，（右旋时不用关心nil节点，可以先去掉，旋完了再补上）

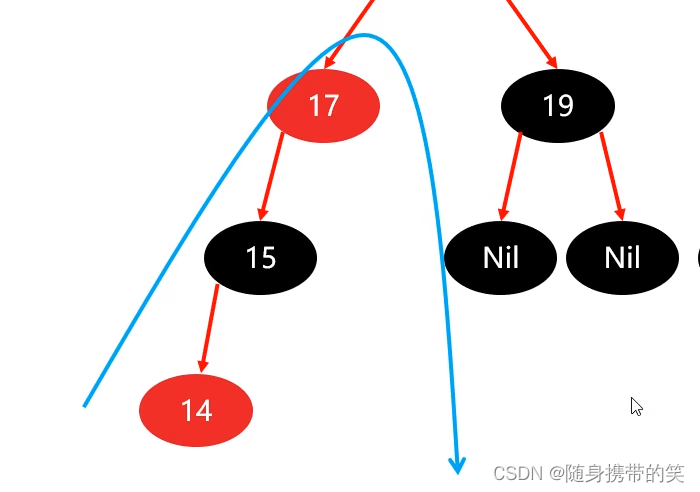
在这里插入图片描述

右旋完毕后如下

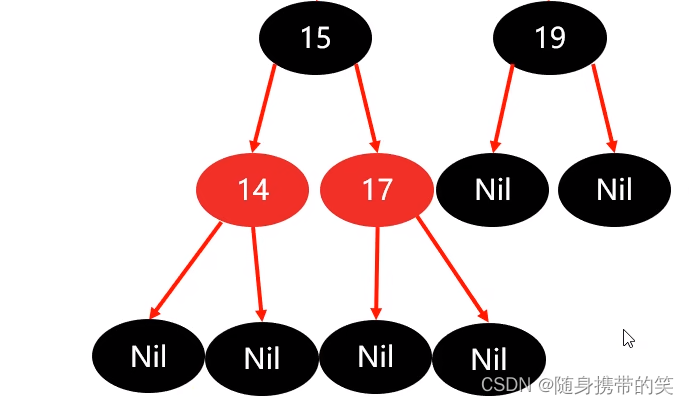
在这里插入图片描述

3.2.3 父红色策略②

最后一种情况
当添加节点为16，按添加规则表上的，走——>非根——>父红色——>③策略

把父节点15作为支点左旋
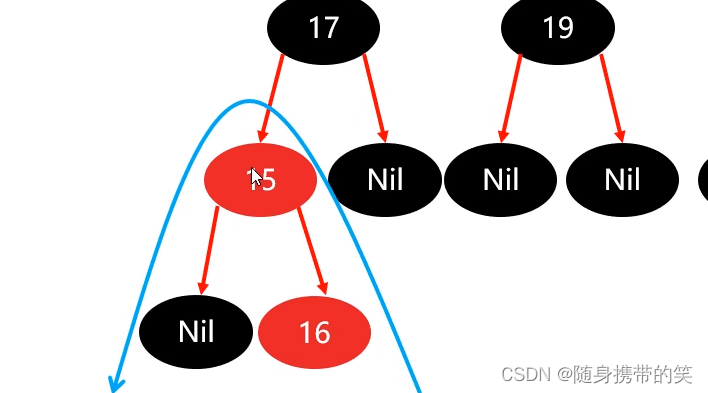
在这里插入图片描述

左旋结果如下
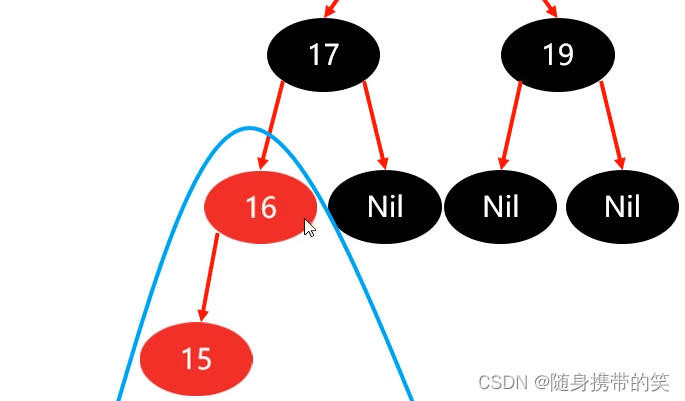
在这里插入图片描述

把父节点15作为当前节点，进行判断（也就是再走一遍规则表）
走的规则路线为：非根——>父红色——>③策略（这就是为什么策略③放在策略②前面写了）

策略③：父节点16设为黑色，祖父17设为红色，以祖父为支点，右旋，结果图如下

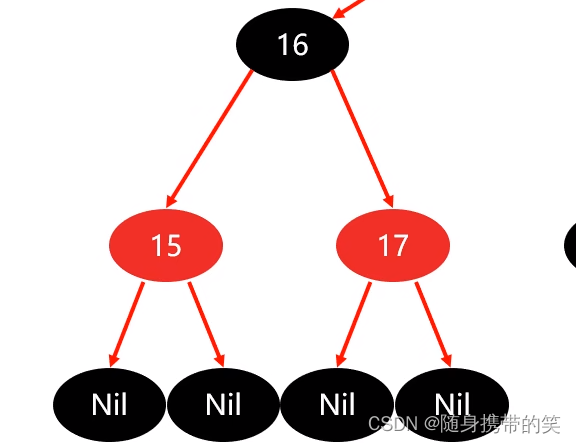
在这里插入图片描述

最后总结红黑树
红黑树的增删改查效率是比较好的，和平衡二叉树不断旋转浪费时间相比，红黑树只改变颜色变量，旋转次数很少，所以效率更高。

至此感谢您的阅览

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

随身携带的笑 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。