leetcode 60 第K个排列-康托展开

最新推荐文章于 2024-07-22 22:57:32 发布

原创最新推荐文章于 2024-07-22 22:57:32 发布 · 271 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

3 篇文章

订阅专栏

博客介绍了LeetCode第60题的解决方案，主要探讨了通过康托展开（Cantor Expansion）来寻找第K个排列的方法。详细解释了回溯法和康托展开的思路，包括如何确定排列的每一位，以及康托展开的计算公式。还给出了康托展开的代码实现。

leetcode 60 第K个排列

1.题目描述

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

“123”
“132”
“213”
“231”
“312”
“321”
给定 n 和 k，返回第 k 个排列。

说明：

给定 n 的范围是 [1, 9]。
给定 k 的范围是[1, n!]。
示例 1:

输入: n = 3, k = 3
输出: “213”
示例 2:

输入: n = 4, k = 9
输出: “2314”

2.解题方法

1.回溯法+减枝

思路分析：

采用DFS深度优先遍历，每层从小到达选择一个数字，利用

visited数组记录每个数字的访问情况，当递归深度超出数组长度

时，找到一种排列组合，序号+1，当前结果序号和目标序号k相同时，

找到结果，设置全局变量退出其他递归函数。

时间复杂度：O(n!)

空间复杂度：

ps:回溯法的时间复杂度过高，会导致超时错误。

2.逆康托法

思路分析：

采用递归的思路，在每一位上确定一个数字，每次确定数字后，

可形成(n-1)!种排列。

k从0开始，

确定第一位：

group = k / (n-1)!, 所以查询结果在组号为group的组中

k = k - group * (n-1)!，更新查询的序号.

例如：

[1,2,3,4], k = 15, n=4

group = up(15 / (3)!) = 3 , 第一位为nums[3-1] = 3，在第三组中

k = 15 % 3！ = 3

确定第二位：

[1,2,4]

group = up(3 / (2)!) = 2 , 第二位为nums[2-1] = 2,在第二组中

k = 3 % 2 = 1

确定第三位：

[1,4]

group = up(1 / (1)!) = 1 , 第二位为nums[1-1] = 1,在第一组中

k = 1 - ((1 / (1)!)*(1!) = 0

确定第四位：

[4]

因为k=0,此时最后一位为nums[0]

1—> (n-1)!

2—> (n-1)!

3—> 1 —> (n-2)!

2 —> 2,1,4 —>(n-3)!

2,4,1

4 —> (n-2)!

4—> (n-1)!

3.代码

import math
class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        res = ""
        #候选数组
        nums = [ i+1 for i in range(n)]
        #求阶乘数组
        facts = [ 1 for i in range(n)]
        fact = 1
        for i in range(n):
            fact *= nums[i]
            facts[i] = fact
        N = n-1
        for i in range(n-1):
            #向上取整求组号，即当前候选数组的数字序号
            group = math.ceil(k/facts[N-1])
            res = res + str(nums[group-1])
            nums.pop(group-1)
            k = k % facts[N-1]
            N = N - 1
        #只剩下一位时，组数一定为1.
        res = res + str(nums[0])
        return res

4.康托展开

康托展开完成了一个全排列到一个自然数的双射，即给出一个排列结果，可以找出此结果是全排列集合中的第几个。反之给出第几个，可以求出全排列的对应排列结果。

本质是计算当前排列在由小到大全排列中的顺序。

具体公式如下：

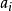表示原数的第i位在当前未出现的元素中是排在第几个（第几组），即比ai小的数字生成的全排列都不考虑，它们的全排列数量= 组数（比ai小的未选数字数目）* 每组元素个数（阶乘）.

例如：

在5个数的排列组合中，计算 34152的康托展开值。

首位是3，则小于3的数有两个，为1和2，，则首位小于3的所有排列组合为
第二位是4，由于第一位小于4，1、2、3中一定会有1个充当第一位，所以排在4之下的只剩2个，所以其实计算的是在第二位之后小于4的个数。因此。
第三位是1，则在其之后小于1的数有0个，所以。
第四位是5，则在其之后小于5的数有1个，为2，所以。
最后一位就不用计算，因为在它之后已经没有数了，所以固定为0
根据公式：

所以比34152小的组合有61个，即34152是排第62。

代码如下：

def kangtuozhankai(nums):
    #  k = a[n]*(n-1)! + a[n-1]*(n-2)! + a[1]*0!
    #  a[n] 表示小于当前位数字的个数
    n = len(nums)
    fact = 1
    facts = [ 1 for i in range(n+1)]
    for i in range(1,n+1):
        fact *= i
        facts[i] = fact

    result = 0
    for i in range(n):
        sum = 0
        for j in range(i+1,n):
            if nums[j]<nums[i]:
                sum += 1
        result += sum * facts[n-1-i]
    return result+1