单链表排序

问题：给定一串单链表，在O(n log n)的时间对链表进行排序。

 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };

解法

1. 使用归并排序，时间复杂度 nlogn。
2. 逐渐分层排序，譬如单链表(3,2,1,4)

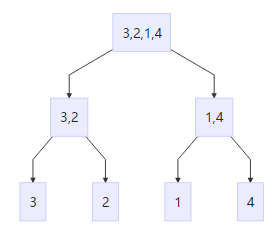
先底层合并使其有序

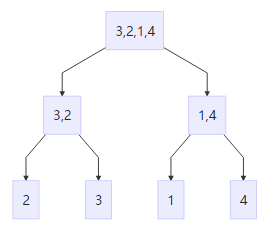
然后同层两两合并

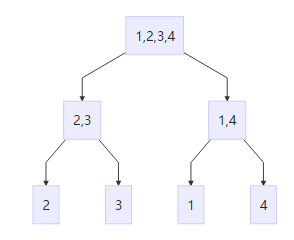
递归解法

递归的关键是要找出中间的位置，这里可以使用快慢指针：
快指针*quick和慢指针*slow，快指针一次走两步，慢指针一次走一步，当快指针到尾的时候，慢指针所指的位置就是链表的中间位置。

首先是合并的方法ListNode *merge(ListNode *left, ListNode *right)

先定义一个头节点headNode方便操作链表，通过改变节点的next指向，合并成一条有序的链。这里需要用到三个指针left，right，p。

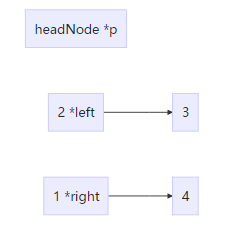
先指向最小值

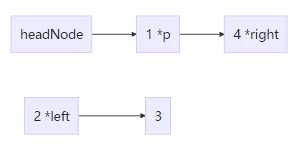
改变next指向

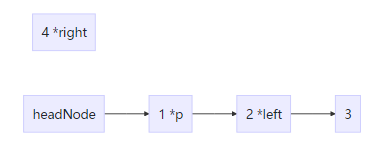
改变next指向

ListNode *merge(ListNode *left, ListNode *right) {
    //头节点，方便操作链表
    ListNode headNode(0);
    ListNode *p = &headNode;
    
    while(left && right) {
        if(left->val < right->val) {
            p->next = left;
            left = left->next;
        }
        else {
            p->next = right;
            right = right->next;
        }
        p = p->next;
    }
    p->next = (left==NULL) ? right : left;
    return headNode.next;
}

主函数：

ListNode *sortList(ListNode *head) {
        if (head!=NULL || !head->next!=NULL) 
            return head;
            
        // 计算中间指针位置
        ListNode *slow = head;
        ListNode *quick = head->next;
        while(slow!=NULL && quick->next!=NULL) {
            slow = slow->next;
            quick = quick->next->next;
        }
        
        //这里需要把链切断，merge再重新合并
        ListNode* right = sortList(head);
        ListNode* right = sortList(slow->next);
        slow->next = NULL;
        
        return merge(left, right);
}

非递归解法

递归解法的空间复杂度并不是常数级，可以使用非递归的解法达到空间复杂度的常数级。

遍历链表，通过不同的跳数来分割链，再把分割出来的链两两合并。

step1: (3),(2),(1),(4)

step2: (2, 3),(1, 4)

setp4: (1, 2, 3, 4)

这里需要增加两个方法，一个是ListNode *cutList(ListNode *head, int step)，一个是ListNode *merge(ListNode *left, ListNode *right)。

1. cutList的作用是根据跳数来分割链并返回下一条链的头指针，譬如一个指向头结点3的指针head，跳数1，则从该链的head后1位开始切断，并且返回最后位的下一个结点。
   

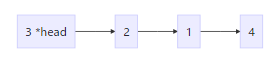
step = 1

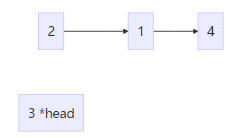
2. merge的作用和递归解法的作用相同:

ListNode *cutList(ListNode *head, int step)
{
    //返回head之后size个node的指针位置,并且把前链切断
    ListNode *p = head;
    while(--step && p!=NULL)
    {
        p = p->next;
    }
    
    if(p == NULL)
        return NULL;
    
    ListNode *q = p->next;
    p->next = NULL;
    return q;
}

ListNode *merge(ListNode *left, ListNode *right)
{
    ListNode headNode(0);
    ListNode *p = &headNode;
    while(left!=NULL && right!=NULL)
    {
        if(left->val > right->val)
        {
            p->next = right;
            p = right;
            right = right->next;
        }
        else
        {
            p->next = left;
            p = left;
            left = left->next;
        }
    }
    p->next = (left==NULL) ? right : left;
    return headNode.next;
}

主函数主要也是使用3个指针：left，right，flagNode。其中left，right分别代表左链和右链，而flagNode则是记录下一次分割链的位置。

譬如当step=2时，left指向1，right指向3，而flagNode则指向5，在left，right合并完成之后直接可以赋值到left链中进行下一轮的合并。

ListNode *sortList(ListNode *head) 
{
    if(!head || !head->next)
        return head;
    
    //设定一个头结点方便操作
    ListNode headNode(0);
    headNode.next = head;
    
    //计算出链表的长度
    int length=0;
    ListNode *p = head;
    while(p != NULL)
    {
        length++;
        p = p->next;
    }
    
    //根据跳数分段合并
    for(int step=1; step<length; step *= 2)
    {
        ListNode* flagNode = headNode.next;
        ListNode* tailNode = &headNode;
        
        while(flagNode != NULL)
        {
            ListNode* left = flagNode;
            ListNode* right = cutList(flagNode, step);
            flagNode = cutList(right, step);
            
            tailNode->next = merge(left, right);
            while(tailNode->next != NULL)
                tailNode = tailNode->next;
        }
    }
    return headNode.next;
}