LeetCode：二叉树最低公共祖先

二叉树最低公共祖先节点又是一道极为经典的算法题，LeetCode第236号题目，同时也是面试官几乎用烂的一个题目，准备跳槽找工作的同学必知必会的一个面试题。

这个题目的要求非常简单，求出给定两个二叉树节点的公共祖先，如下所示的二叉树，那么节点5和节点1的3，我们该怎样解决这个问题呢？

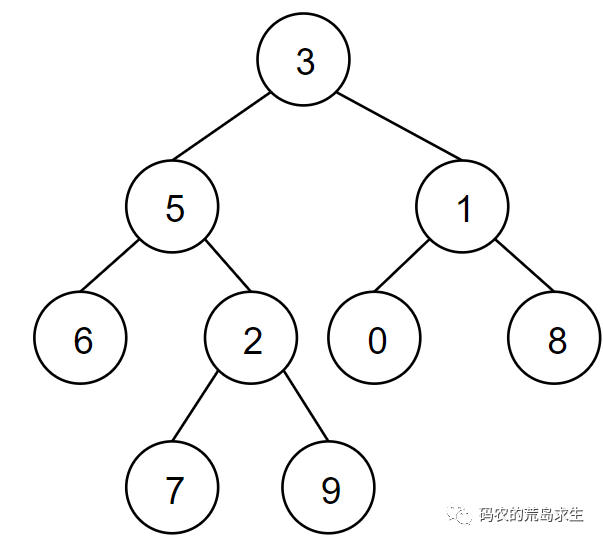
如何确定两个节点的公共节点？

这个问题的关键点在于我们怎么就能确定某个节点是给定条件下的公共节点，从图中我们能快速的知道节点5和节点1的公共节点是3，节点6和节点7的公共节点是5，问题是你有没有想过，你的大脑是如何知道节点6和节点7的公共祖先是5的？如果你能清晰的描述清楚这个过程，那么代码自然就能写出来了。

我们来看看为什么节点6和节点7的最低公共祖先是5。其实很简单，原因就在于节点5和左子树中包含了节点6，节点5的右子树中包含了节点7；也就是说只要我们找到了一个节点，其左右子树中分别包含了两个给定的节点，那么这个节点就是我们要找的答案。

意识到以上的关键就在于你要去想“为什么你的大脑知道节点6和节点7的公共祖先是5”，你的大脑是如何找到答案的？实际上你的大脑是这样找到答案的：

• 找到节点6的所有祖先节点，也就是5和3

• 找到节点7的所有祖先节点，也就是2、5和3

那么很显然节点6和节点7的所有祖先节点从5开始就一样了，因此节点5就是最低公共节点，如图所示：

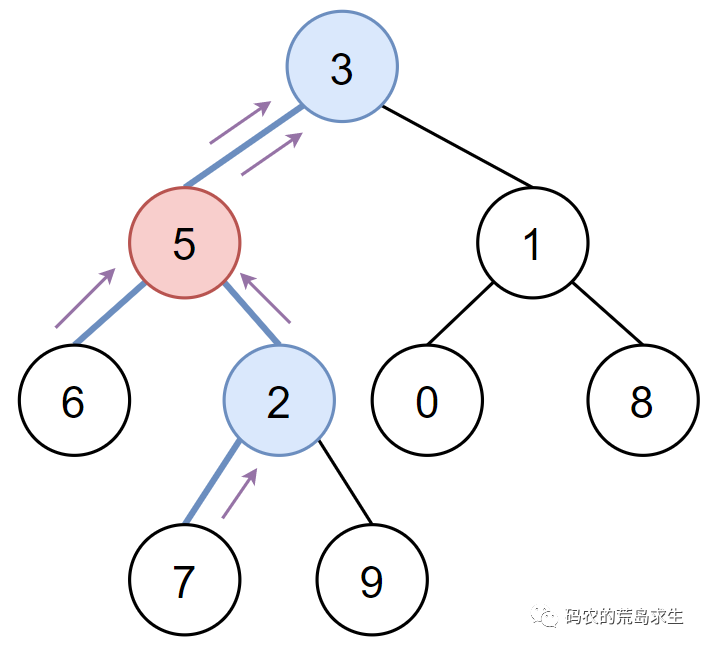
此外我们还要考虑这样的特殊情况，那就是给定两个节点5和2，那么这两个节点的最低公共祖先节点是5，实际上这个特例并没有逃脱上述推导过程，你可以简单的认为一个节点的最低祖先其实是自己，由于节点5就是题目中给定的一个节点，而5的右子树中又包含2，那么5就是这两个节点的最低公共祖先。

现在让我们总结一下，什么样的节点才是我们需要找的最低公共祖先节点？

• 如果一个节点的左子树和右