字符串匹配算法之KMP算法

第一次写技术博客，选择写KMP算法的原因是这是我接触比较久的一个算法，因为比较抽象，之前一直没弄懂它，后来参阅了相关的资料，似乎懂了点不久就又忘没了，终于在参阅了《算法导论》及各大技术博客之后，想把自己对KMP算法的理解写下来。

字符串匹配问题形式化定义如下：假设文本是一个长度为n的数组T [1…n]，而模式是一个长度为m的数组P[1…m]，其中m<=n，P 和T 都是来自一个有限字母集的字符。如果模式P在文本T中出现，且偏移为s，则称s为一个有效偏移，否则成为无效偏移。字符串匹配问题就是找到模式P在文本T中的所有有效偏移。下图即是一个字符串匹配的例子。

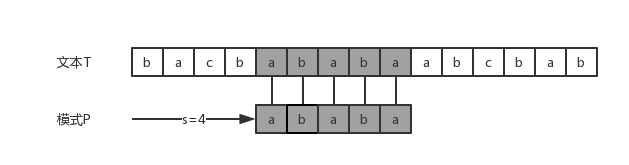
算法思想

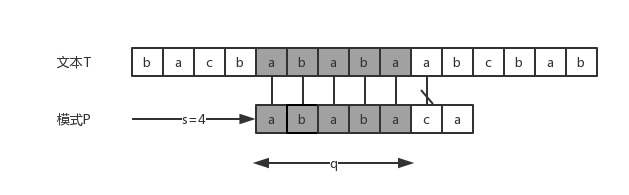
我们考察一下朴素字符串匹配算法的操作过程，上图展示了一个文本T与模式P匹配的过程，在这个例子中，q=5个字符已经匹配成功，但模式的第六个字符不能与相应位置的文本字符匹配，可见偏移s=4是一个无效偏移，这时一个很自然的想法是令偏移加1，即s=4+1，然而实际上这仍然是一个无效偏移，因为模式P的前四个字符abab与文本T中相应位置的子串baba不相同。细心的你会发现这四个字符包含在已经匹配成功的q个字符中，如果我们简单地在偏移s无效的情况下直接考察偏移s+1，显然我们就忽视了已经匹配成功的前q个字符可能给我们带来的某些有用的信息，所造成的后果就是带来了较高的时间复杂度O($n\ast m$)。实际上，q个字符已经匹配成功的信息确定了相应的文本字符，而这q个已知的文本字符使我们能够立即确定某些偏移是无效的，如偏移s=4+1是无效的，偏移s=4+2 可能是有效的。那么这q个字符是如何给我们提供这样信息的呢？

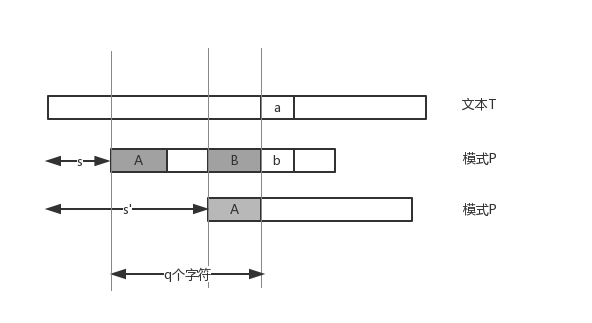
如上图所示，当匹配到第q+1个字符时两个字符不相等，所以偏移s是无效偏移，这时需要将模式串P向前移动，那么移动到哪里合适呢？下一个要考察的偏移可以是$s^{\prime }=s+1$，也可是是$s^{\prime }=s+q$，或者两者之间，但不可以$s^{\prime }>s+q$（这是显然的），所以我们要在 s+1~s+q之间找下一个可能的有效偏移，即上文提到的“合适”的位置。如上图第三行，当偏移s无效时，模式串P向前移动到偏移s’，显然偏移s’是有效偏移的必要条件是A=B，如果A!=B，那么s’一定无效偏移，所以我们要找的“合适”的位置，是向前移动模式串P到第一个满足A=B的位置，而这个位置就是A和B是P[1…q]的最长公共前后缀（不算该串本身）的位置，我们表示为next[q]，当知道了这个最长公共前后缀的长度，就可知直接将模式串向前移动 $q-next[q]$ 位，接着继续比较下一个位置。然后我们便可以直接从文本T中的“a”开始比较，即文本T中已经比较过的位置不需要在再比较，算法的复杂性显然是$O(n)$，这就是KMP算法的思想。了解了KMP的思想，我们知道首先要做的就是先求出模式穿P每个位置的最长公共前后缀长度，后面我们会看到该过程的时间复杂度是$O(m)$，所以KMP算法的时间复杂度是$O(n+m)$。

计算next数组

长度为1的字符串的最长公共前后缀的长度为0，即$next[1]=0$假设我们已经求得next[1]，next[2]，，，next[q]，分别表示长度为1到i的字符串的最长公共长度，现在要求next[q+1]。

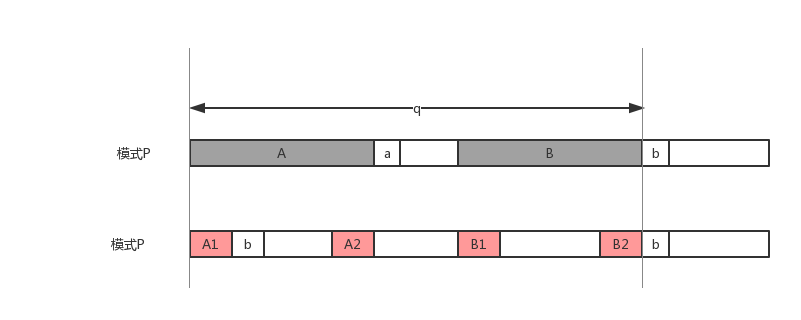
如上图所示，假设A和B是P[1…q]的最长公共前后缀（即A=B），如果a=b，则显然$next[q+1]=next[q]+1$；如果 $a\ne b$ 怎么办呢，我们可以考察串A的最长公共前后缀A1和A2，因为$A1=A2$，$B1=B2$，$A=B$，所以$A1=B2$，因此如果此时A1的下一个字符等于b，那么next[q+1]=next[ next[q] ]+1，如果不相等，我们就继续考察A1的公共前后缀，直到不能分割为止。如果分割到不能再分，那么next[q+1]显然为0了。
求next数组的代码如下：

const int MAXN = 100;
//next[x]表示前x个字符的最长公共前后缀。
//显然下标从1开始是有意义的，为了方便我们置next[0]=0。
int next[MAXN];
void getNext(string str) {
    next[0] = next[1] = 0;
    int comLength = 0;
    //i为字符串下标，字符串编号从0开始。
    for(int i = 1; i < str.size(); i++) {
        //设str前i个字符为substr
        //如果substr存在公共前后缀（comLength > 0），
        //并且前缀的下一个字符不等于substr的下一个字符(str[i] != str[comLength])
        while(comLength > 0 && str[i] != str[comLength]) {
            //更新最长公共前后缀
            comLength = next[comLength];
        }
        if(str[i] == str[comLength]) {
            comLength++;
        }//else comLength一定是0
        //计算str[0-i]子串的最长公共前后缀
        next[i + 1] = comLength;
    }
}

KMP算法代码

有了求next数组的代码，我们接下来给出KMP算法代码如下，我么可以看到，模式串P的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较P和T即可达到模式串P前移的目的。
注:上文的算法描述中next数组和字符串的下表都是从1开始，代码中next数组下标仍然从1开始，但是字符串下标出于习惯从0开始，希望不会引起不必要的混淆。

//pattern在text中出现的位置
void kmp(string text, string pattern) {
    //q为已匹配的字符串长度
    int q = 0;
    //遍历text
    for(int i = 0; i < text.size(); i++) {
        while(q > 0 && text[i] != pattern[q]) {
            q = next[q];//下一个字符不匹配
        }
        if(text[i] == pattern[q]) {
            q++;//下一个字符匹配
        }
        if(q == pattern.size()) {//整个pattern都匹配了
            cout << "Pattern occurs with shift " << i - q + 1 << endl;
            q = next[q];//寻找下一次匹配
        }
    }
}

int main() {
    string text, pattern;
    cin >> text >> pattern;
    getNext(pattern);
    kmp(text, pattern);
    return 0;
}