马尔可夫决策和贝尔曼方程

马尔可夫决策和贝尔曼方程

一、什么是马尔可夫性、马尔可夫过程和马尔可夫决策过程

1） 马尔可夫性是指当前状态s包含了过去所有的历史信息，由当前决定未来；
2） 马尔可夫过程，就是具有马尔可夫性的随机过程（通常由链表示，也叫马尔科夫链），仅包含状态、状态到状态的转移概率；
3） 马尔可夫决策过程，是根据马尔可夫过程按照策略做出决策，由（S\A\R\P\gama）组成；

二、对于一个马尔可夫决策过程，R有限时，状态转移函数和回报函数

1） 状态转移函数

`
PI（a|s）表示在当前状态s下，采取动作a的概率，也就是决策（概率），那么从状态s跳转到s’就为采取能够跳转到s‘的动作a的概率和采取动作a后能够从s成功跳转到s’的概率之积；当前状态s下有很多a可以行动（例如a1,a2），并都可以跳转至s’，只不过他们跳转的概率不同，可能a1对应的跳转概率大一些，那么求和就可以得到当前策略PI下，由当前状态s跳转到状态s’的概率；

2）回报函数

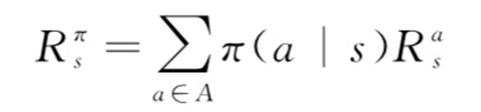
当前状态s下采取行动a，环境会给出一个立即回报R（a|s），个行动a下的回报和就是针对当前策略PI下的立即回报；

三、贝尔曼期望方程和贝尔曼最优方程的数学描述

1）贝尔曼期望方程

首先讲什么是值函数，又分为状态值函数V（s），表示当前状态s所具有的价值；行为值函数Q（s,a），表示当前状