代码随想录训练营Day20 二叉树 part06 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树

654.最大二叉树

题目链接：654. 最大二叉树 - 力扣（LeetCode）

文章链接：代码随想录 (programmercarl.com)

视频链接：又是构造二叉树，又有很多坑！| LeetCode：654.最大二叉树

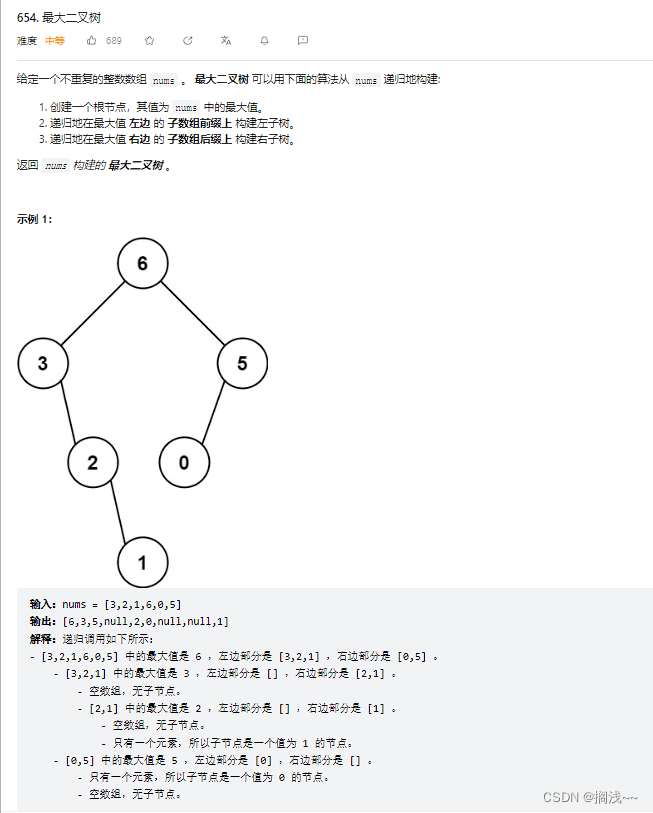
 这道题难点有二，一、如何构建二叉树。二、如何找最大值

难点一：构建二叉树，如果做了leetcode 106 就很好理解，所有构建二叉树的题目都可以使用前序递归的方法，这道题也不例外。那么递归三部曲就很自然的出来了。

a.确定递归参数和返回值，我们需要通过一个数组来构建二叉树，所以参数就是数组形式，我们这里使用vector。构建二叉树，返回的自然就是二叉树的节点了。代码如下：

TreeNode* constructMaximumBinaryTree(vector<int>& nums)

b.确认递归的终止条件。什么时候中止递归，当然就是递归到子节点的时候，而到子节点的时候就是数组里只有这个元素的时候，也就是元素数量为1时，即为终止条件。

if(nums.size()==1)
        {
            node->val=nums[0];
            return node;
        }

c.确认单层递归的逻辑。用中文描述也很简单，（但不一定能听懂）。最大二叉树构造逻辑就是先找到数组中的最大值为父节点a，这个元素a左边的元素构成一个新的数组，找到最大值即为a的左节点b,a右边的元素也构成一个新的数组，找到最大值即为a的右节点c。接着一直递归下去，直到终止。

代码如下：

int index=0;
        int max=0;
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]>max)
            {
                max=nums[i];
                index=i;
            }
        }
        node->val=max;//将数组中的最大值赋值给节点的数值
        if(index>0){
            vector<int> left(nums.begin(),nums.begin()+index);//构建新数组
            node->left=constructMaximumBinaryTree(left);//左递归
        }
        if(index<nums.size()-1){
            vector<int> right(nums.begin()+index+1,nums.end());//构建新数组
            node->right=constructMaximumBinaryTree(right);//右递归
        }
        return node;

总代码如下:

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node=new TreeNode(0);//建立二叉树新节点
        if(nums.size()==1)//数组元素只剩一个，就终止
        {
            node->val=nums[0];
            return node;
        }
        int index=0;
        int max=0;
        for(int i=0;i<nums.size();i++)//循环找到数组中的最大值
        {
            if(nums[i]>max)
            {
                max=nums[i];
                index=i;//记录最大值的下标
            }
        }
        node->val=max;//将最大值赋值给节点的数值
        if(index>0){
            vector<int> left(nums.begin(),nums.begin()+index);//建立左数组
            node->left=constructMaximumBinaryTree(left);//进行左递归
        }
        if(index<nums.size()-1){
            vector<int> right(nums.begin()+index+1,nums.end());//建立右数组
            node->right=constructMaximumBinaryTree(right);//进行右递归
        }
        return node;//返回二叉树节点
    }
};

 617.合并二叉树 

 题目链接：617. 合并二叉树 - 力扣（LeetCode）

文章链接：代码随想录 (programmercarl.com)

视频链接：一起操作两个二叉树？有点懵！| LeetCode：617.合并二叉树 

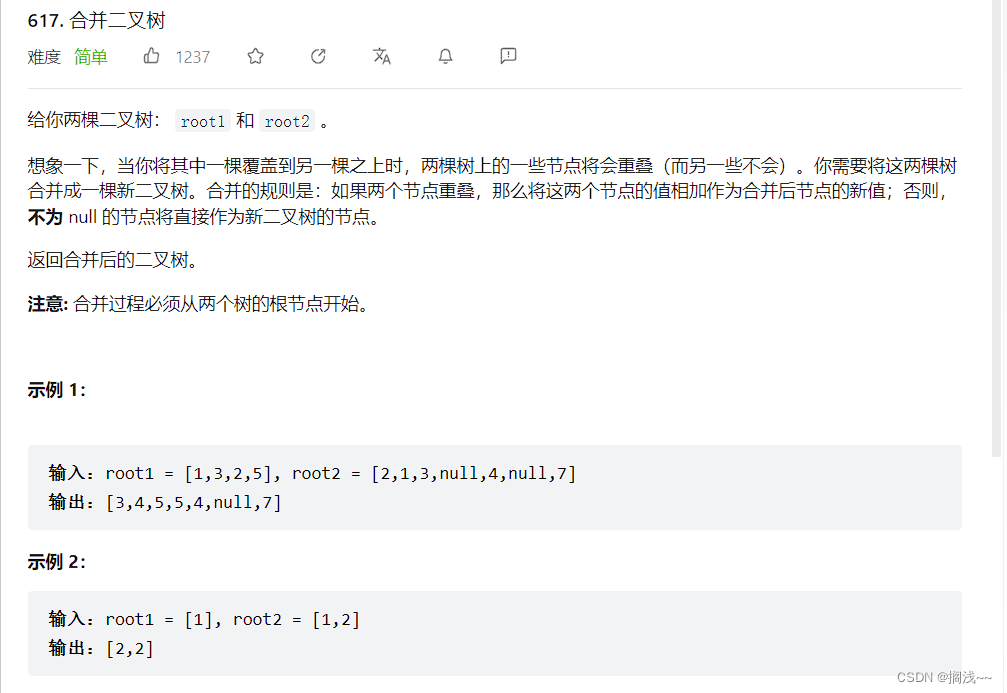
这道题其实难度也不大，递归解决的也很轻松，依旧是万能的递归三部曲。

a.确认递归参数和返回值，合并二叉树，参数自然就是两个二叉树的节点了，返回值自然就是新形成的二叉树的节点了。

TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2)

b.确认递归的终止条件。啥时候终止？我们需要分类讨论，1.如果同一位置，一个二叉树没有节点而另一个二叉树有节点，那么就直接返回那个有节点的二叉树节点就好了。2.要么就是递归到到头了，一个return 返回新形成的节点就行。

if(root1==NULL) return root2;
if(root2==NULL) return root1;

c.确认单层递归的逻辑

这道题的逻辑也不难理解，就是将两个节点的值相加然后赋值给一个新的节点。然后按着中左右的顺序，指针不断指向子节点，形成递归。代码如下：
 

root1->val+=root2->val;
root1->left=mergeTrees(root1->left,root2->left);
root1->right=mergeTrees(root1->right,root2->right);
return root1;

总代码如下：

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1==NULL) return root2;//直接返回有元素的节点
        if(root2==NULL) return root1;
        root1->val+=root2->val;中处理
        root1->left=mergeTrees(root1->left,root2->left);左递归
        root1->right=mergeTrees(root1->right,root2->right);右递归
        return root1;返回节点
    }
};

 700.二叉搜索树中的搜索

 题目链接：700. 二叉搜索树中的搜索 - 力扣（LeetCode）

文章链接：代码随想录 (programmercarl.com)

视频链接：不愧是搜索树，这次搜索有方向了！| LeetCode：700.二叉搜索树中的搜索

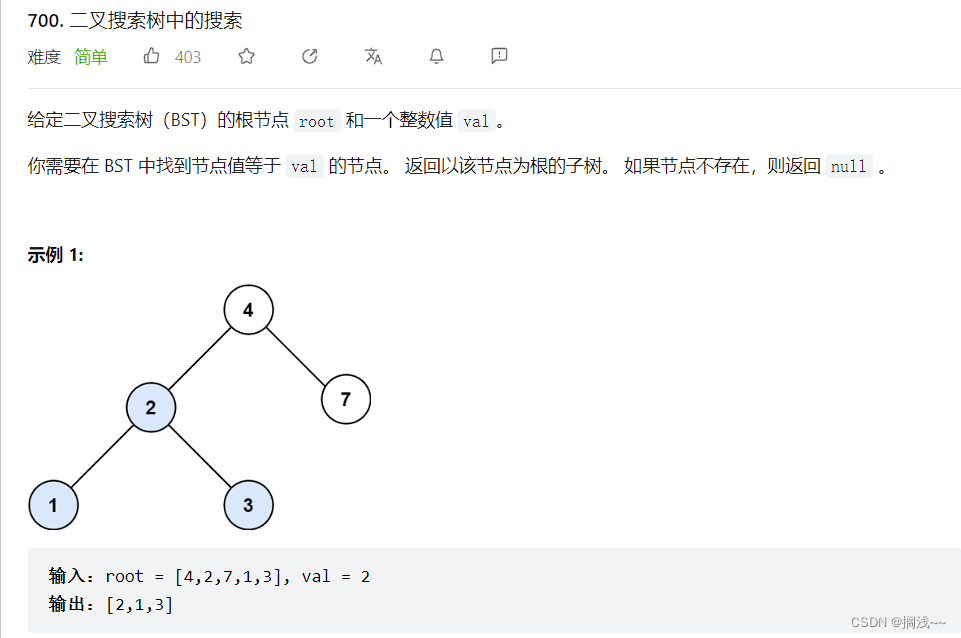
 这道题想法不难，不就是递归来遍历嘛，直到找到val,找不到就return NULL。我觉得这道题主要考了二叉搜索树的性质，一个父节点，它的左子节点一定比父节点小，右子节点一定比父节点大，所以我们就不用无脑遍历了，可以进行一定的剪枝处理。如果val比节点值要大，那就遍历它的右子树，如果小，就遍历左子树。代码如下：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root==NULL||root->val==val) return root;//终止条件，遍历到子节点或者符合条件的节点
        TreeNode* result=NULL;
        if(root->val>val) result=searchBST(root->left,val);
        if(root->val<val) result=searchBST(root->right,val);
        return result;
    }
};

98.验证二叉搜索树

 题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

文章链接：代码随想录 (programmercarl.com)

视频链接：你对二叉搜索树了解的还不够！ | LeetCode：98.验证二叉搜索树

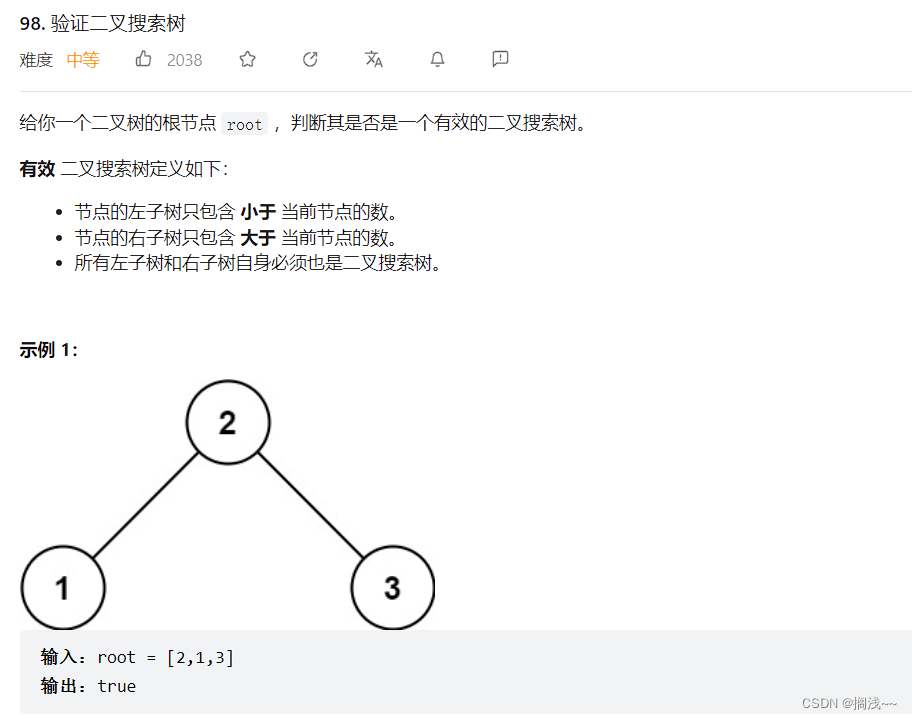
这道题主要考察的就是搜索二叉树的性质，通过定义，我们可以了解，如示例一，左子节点的数值<父节点的数值<右子节点的数值。通过这个性质，我们可以通过左中右的顺序，使用中序递归将二叉树的节点元素放入一个数组中。按照二叉树的性质，所形成的数组一定是从小到大排列的。接下来，我们就可以来检验数组是否按升序排列，如果不是就代表不是搜索二叉树。

代码如下：

 

class Solution {
public:
    vector<int> vec;
    void traversal(TreeNode* root){//通过中序递归，将二叉树中的元素加入到数组中
        if(root==NULL) return;
        traversal(root->left);
        vec.push_back(root->val);
        traversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
        traversal(root);
        for(int i=1;i<vec.size();i++){//检验数组元素大小是否是升序
            if(vec[i]<=vec[i-1]) return false;
        }
        return true;
    }
};

Day20 打卡成功，耗时2.5个小时，再接再厉哈，不知道是题目简单一点了，还是自己真的懂了点了，还是比较轻松的。