1、线性结构

一、定义

• 1、存在唯一的 第一个和最后一个元素
• 2、处理唯一性元素外，其余元素有且只有一个 直接前驱和直接后继元素

一、存储结构

1、线性结构

• 1、逻辑上和物理上都是相邻的

• 2、存储位置

• $$LOC(a_i)=LOC(a_1)+(i-1)\ast L$$

• 3、优点是查找、缺点是插入和删除

• 4、插入元素需要移动元素的期望值
  $$E_{insert}=\sum _{i=1}^{n+1}{P}_i\ast (n-i+1)=\frac{1}{n+1}\sum _{i=1}^{n+1}{P}_i\ast (n-i+1)=\frac{n}{2}$$
  $$P_i为位置i插入新元素的概率$$

• 5、插入元素需要移动元素的期望值
  $$E_{delete}=\sum _{i=1}^n{q}_i\ast (n-i)=\frac{1}{n}\sum _{i=1}^{n+1}{q}_i\ast (n-i)=\frac{n-1}{2}$$
  $$q_i为删除第i个元素的概率$$

2、链式结构

• 1、通过指针对节点进行访问

typedef struct node {
  int data ;
  struct node * next ;
}NODE , *LinkList ;

• 2、操作
  
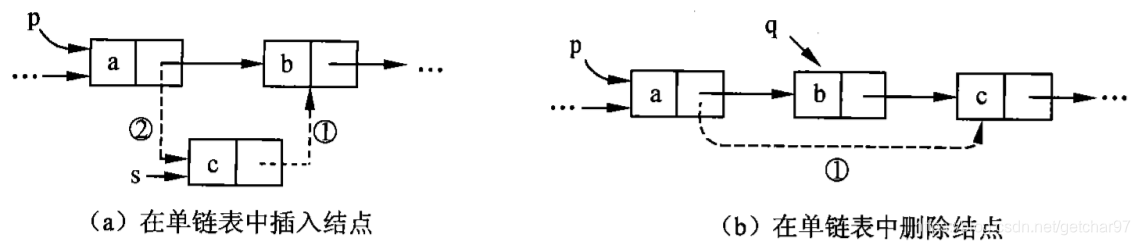
• 3、操作

查

/**在链表中查找 值为k 的元素 */
LinkList Find_List_Value(LinkList L, int k) {
  LinkList p;
  p = L->next; // 初始化临时指针   如果不进行初始化 ，会改变原指针 而且 链表带空的头结点
  while (p) // 只要p不为空往下找
  {
      if (p->data == k) // 说明找到了值
      {
          break;
      } else {
          p = p->next; // 往下继续找
      }
  }
  return p; // 如果找到了， 则p 是一个带有值得节点，如果没有找到，则 p 为NULL
}
  /**在链表中查找 第k个 的元素 */
LinkList Find_List_Site(LinkList L, int k) {
  LinkList p  ,int i ;
  p = L->next; // 初始化临时指针   如果不进行初始化 ，会改变原指针 而且 链表带空的头结点
  i = 1 ;
  while (p && i < k) // 只要p不为空往下找
  {
    p = p->next; // 往下继续找
    i ++ ;

  }
  if(p&& i == k){
      return p ;  // 如果找到了， 则p 是一个带有值得节点
  }
  return NULL; //如果没有找到，则 p 为NULL
}

增

 // 在第k 个位置插入值为value 
	int Insert_List(LinkList L, int k, int vlaue) {
  LinkList p, s;
  if (k == 1) { // 首插入
      p = L;
  } else {
      p = Find_List_site(L, k - 1);
  }
  if (!p) {
      return -1;
  } else {
      s = (NODE *)malloc(sizeof(NODE));
      if (!s) {
          return -1;
      }
      s->data = vlaue;
      s->next = p->next;
      p->next = s;
      return 0;
  }
 }

删

int Delete_LinkList(LinkList L ,int k){
   LinkList p, s;
   if (k == 1) { // 首插入
       p = L;
   } else {
       p = Find_List_site(L, k - 1);
   }
   if(!p || !p->next ){
       return -1 ;
   }
   s = p->next ;
   p->next = s->next  ;
   free(s) ;
   return 0 ;
}