很显然神经网络的节点数越少网络的迭代速度越快,那在保证准确率的前提下隐藏层节点数最少可以是多少个?本文搭建了一个81*n*2的神经网络通过改变n的值测量这个网络的隐藏层节点数量的极小值。
使用的训练集和测试集是mnist的0和1,经过1/3的池化变成9*9的图片,每个n值进行200批,每10批测量一次准确率。每批的batchsize是20个用放回取样,每批迭代1000次。学习率是0.1,没有偏置,激活函数用sigmoid,并同时统计每批次的运行时间。
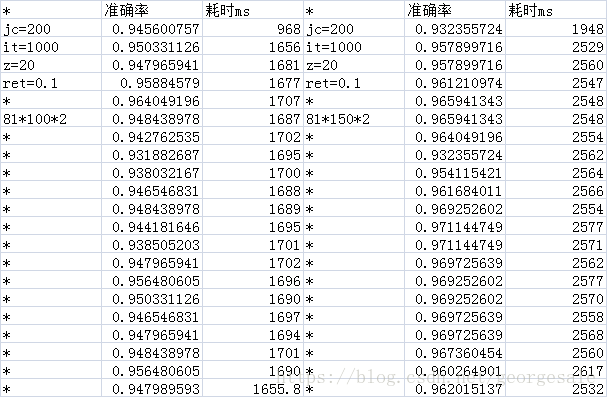
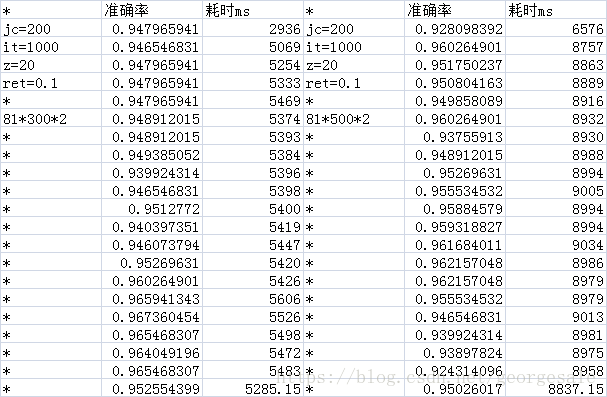
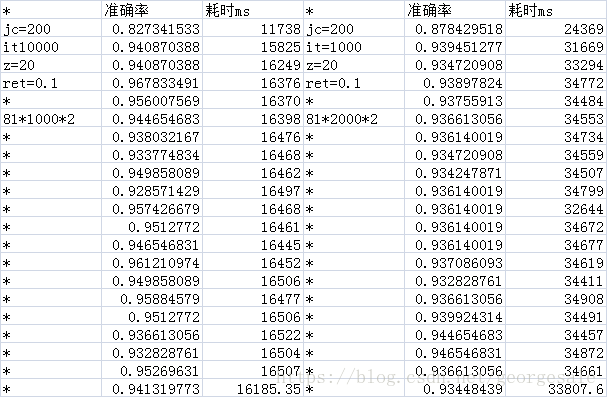
得到的数据
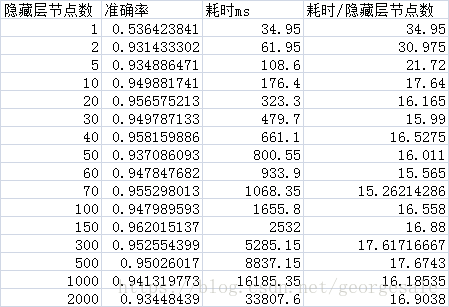
测量的数据表明对于这个81*n*2的网络的隐藏层节点数最小值可以是2,还是挺令人震惊的的,也就是81*2*2的网络就可以运行准确率可以达到93%和81*50*2的网络的性能差不多,但是时间只有81*50*2的0.076,也就是说用81*2*2的网络比81*50*2的网络可以省下92%的时间。
特别是隐藏层的节点数是2000时的耗时是2的耗时的554倍但是81*2000*2的准确率是93.4%和81*2*2的准确率93.1%,也差不多,每次运算多消耗了554倍的时间性能确没有提升。
一个非常明显的规律是当隐藏层节点数大于20个以后平均每节点耗时大约都是16.44ms左右的定值,也就是说当节点数大于20个以后网络的耗时基本上可以按照
耗时=n*16.44的公式算出来。
但是网络的性能确没有增加,
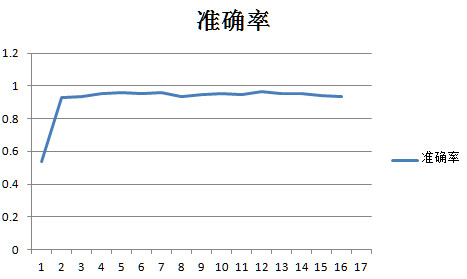
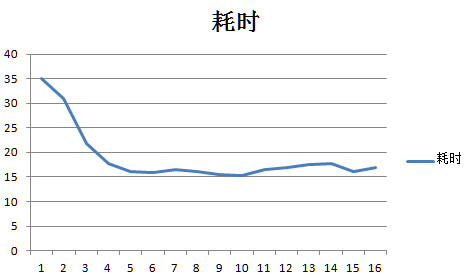
所以可以按照耗时曲线找到拐点附近的点就是用时最少,同时性能也有保证的隐藏层节点数量。比如这道题就是20个节点左右耗时曲线的第5个点。
原始数据
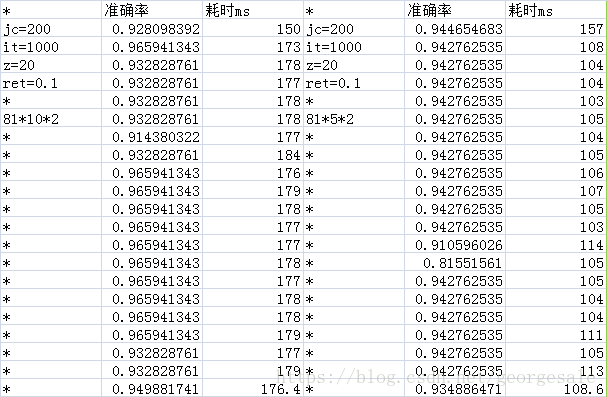
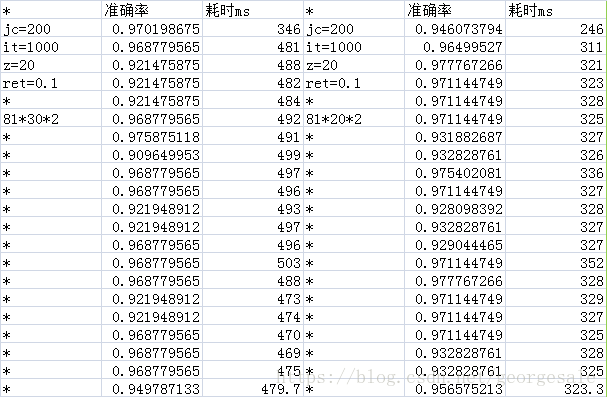
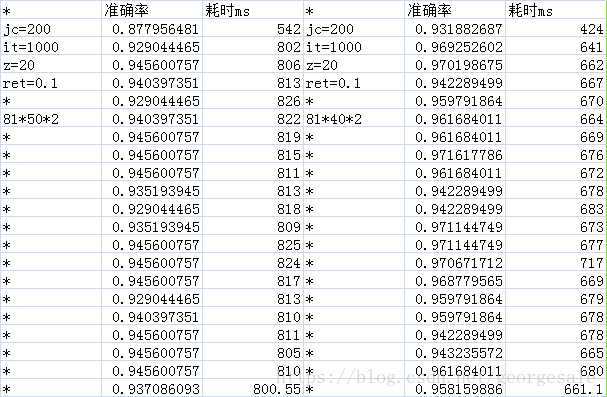
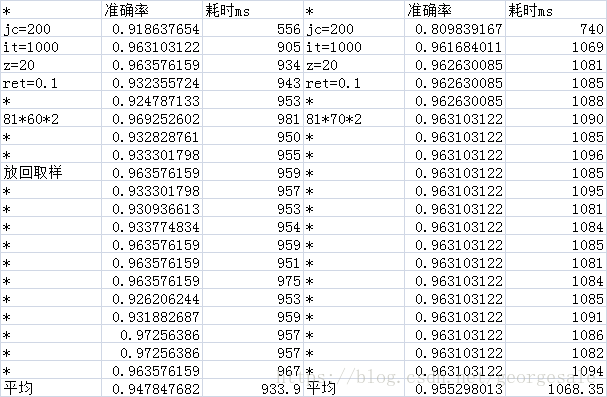





 本文通过实验发现,对于特定任务(MNIST手写数字0和1的识别),即使将隐藏层节点数减少到2个,神经网络仍能达到93%的准确率,其性能与节点数为50时相近,但运行效率提高了92%。
本文通过实验发现,对于特定任务(MNIST手写数字0和1的识别),即使将隐藏层节点数减少到2个,神经网络仍能达到93%的准确率,其性能与节点数为50时相近,但运行效率提高了92%。

















 970
970












