基于迭代次数和分类准确率的两种排序

(A,B)---81*30*2---(1,0)(0,1)

让分类原点A为mnist的0，分类对象B是1-9，固定收敛误差，统计迭代次数，并将迭代次数作为B到A的距离，得到数轴

A	5	7	2	4	3	9	1	6	8
0	5402.955	7822.01	8358.603	11983.15	12572.23	13346.79	23558.45	25605.5	27905.07

在一个二分类网络中，分别统计(1,0)位和(0,1)位的分类准确率，并统计差值，就可以得到分类过程中错误图片的流量和流向。得到表格

		平均准确率	1-0	0-1			错误图片流量
0	8	0.98042272	0.989943	0.970511	0.010057	0.029489	-0.01943216
0	9	0.98506133	0.992976	0.976753	0.007024	0.023247	-0.01622312
0	7	0.99210495	0.993565	0.990248	0.006435	0.009752	-0.00331658
0	6	0.98371182	0.984386	0.982644	0.015614	0.017356	-0.00174171
0	1	0.99692903	0.994635	0.998824	0.005365	0.001176	0.004188945
0	3	0.98356606	0.980638	0.986101	0.019362	0.013899	0.005462312
0	4	0.98729595	0.97602	0.998177	0.02398	0.001823	0.022156784
0	2	0.97430592	0.961937	0.986285	0.038063	0.013715	0.024348744
0	5	0.96506537	0.943022	0.986723	0.056978	0.013277	0.043700503

与前文不同，这次实验测试集与训练集相同，都是前5000张图片。因此平均分类准确率等于两个位的平均值，

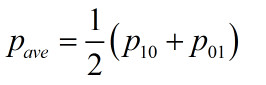
比较两个表格，得到了两组不同的排序

错误图片流量
	8	9	7	6	1	3	4	2	5
0	-0.01943	-0.01622	-0.00332	-0.00174	0.004189	0.005462	0.022157	0.024349	0.043701
迭代次数
	5	7	2	4	3	9	1	6	8
0	5402.955	7822.01	8358.603	11983.15	12572.23	13346.79	23558.45	25605.5	27905.07

迭代次数排序与错误图片流量排序是不一样的。如果迭代次数越大表明二者差异越小，那错误图片流量越小似乎也应该表明二者差异越小，所以为什么两组排序不一致？

对这两种不同排序的一个可能解释，这应该是两个不同的作用过程，错误图片流量表达的相互作用是分类对象B与（A，B）组成的整体之间的相互作用，表达的是在（A，B）这个整体中B与A和B与B的相似性。

而迭代次数表达的相互作用是A与B之间的相互作用，表达的A与B之间的差异，因为这里A与B都是不可分的，因此迭代次数不可细分，也没有方向。因此B与（A，B）中B的差异的排序与B与A之间差异的排序是可能不同的。

这两种差异都可以用来分类图片，用迭代次数法的好处是不必训练网络，但需要知道整个形态数轴。而用分类准确率的方法虽然不必了解形态数轴，但需要制备所有的测试集并训练网络。