[NOI2003] 木棒游戏 题解

题目背景

这是一个很古老的游戏。用木棒在桌上拼出一个不成立的等式，移动且只移动一根木棒使得等式成立。现在轮到你了。

题目描述

你只能移动用来构成数字的木棒，不能移动构成运算符（+、-、=）的木棒，所以加号、减号、等号是不会改变的。移动前后，木棒构成的数字必须严格与图2中的0~9相符。如果移动一根木棒可以使等式成立，则输出新的等式，否则输出No。

输入格式

输入数据要符合逻辑。字符串的长度小于等于1000。

输出格式

如果有解，则输出正确的等式，格式与输入的格式相同（以“#”结尾，中间不能有分隔符，也不要加入多余字符）。此时输入数据保证解是唯一的。

如果无解，则输出“No”（N大写，o小写）。

输入输出样例

输入 #1复制

1+1=3#

输出 #1复制

1+1=2#

一道简单的模拟题

首先我们来看一下题

"与图2中的0~9相符"

??? 图呢

根据我们的生活经验，我们知道0→90→9应该是这么摆的：

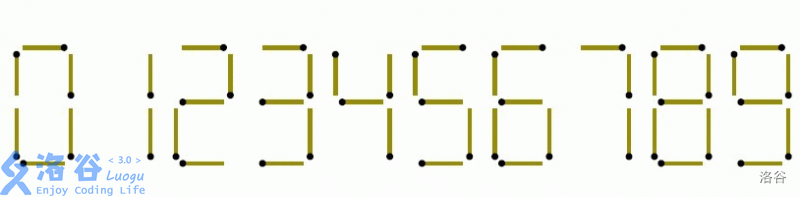
首先我们发现，题目中不能移动构成运算符（+、-、=）的木棒 ，因此我们不管怎么移动数字的木棒，这个数的加、减和位数是不变的。我们如果把所有的数字都按照位数拆开来，以样例为例

11+77=34

变成

1*10+1*1+7*10+7*1=3*10+4*1

那么不管数字怎么变，它后面乘的多少是不会变的，因此我们可以提前处理好。然而在等号两边让我们看起来很不爽，反正符号不会变，我们可以通过初中知识移项将其全部移到一遍就ok了

1*10+1*1+7*10+7*1-3*10-4*1=0

那我们现在只需要通过更改上式中任意两个第一项使其成立就做完了

我们知道n≤1000n≤1000，因此我们完全可以枚举两个数，然后考虑移动火柴带来的情况，在判断是否成立

由于我比较懒，用了一种常数较大的O(n2)O(n2)算法，即选一个有火柴的地方，在选取一个没有火柴的地方，移动火柴，判断式子是否成立（其实这么做枚举了很多不必要的情况）

对于一个数字，选择用状压去描述，如果有第ii根火柴，二进制下第ii位就是11，反之为00

当对第ii根火柴进行更改时，就把数字⊕2i⊕2i即可

具体实现可以参考代码

#include<bits/stdc++.h>
char ch[2000];
const int n[10]={0b1111011,//0
				 0b1001000,//1
				 0b0111101,//2
				 0b1101101,//3
				 0b1001110,//4
				 0b1100111,//5
				 0b1110111,//6
				 0b1001001,//7
				 0b1111111,//8
				 0b1101111//9
				 };
struct num{//数字 
	int val;//权值 
	int des;//描述
	/*
	 _   1
	|_|  2 3 4
	|_|  5 6 7 
	*/
	/*                  7 6 5 4 3 2 1
	1  4 7              1 0 0 1 0 0 0
	2  1 3 4 5 6        0 1 1 1 1 0 1
	3  1 3 4 6 7        1 1 0 1 1 0 1
	4  2 3 4 7          1 0 0 1 1 1 0
	5  1 2 3 6 7        1 1 0 0 1 1 1
	6  1 2 3 5 6 7      1 1 1 0 1 1 1
	7  1 4 7            1 0 0 1 0 0 1
	8  1 2 3 4 5 6 7    1 1 1 1 1 1 1
	9  1 2 3 4 6 7      1 1 0 1 1 1 1
	0  1 2 4 5 6 7      1 1 1 1 0 1 1
	*/
	bool check(){//检验是否合法 
	 	for(int i=0;i<10;i++)
	 		if(val==n[i])
	 			return true;
	 	return false;
	}
	bool check(int w){//检验第w根是否存在 
		if(val>>w&1!=0)return true;
		return false; 
	}
	bool change(int w){//更改w根的位置 
		val^=(1<<w);
	}
	int get(){
		for(int i=0;i<10;i++)
			if(val==n[i])
				return i;
	}
	num(int _N=0,int Wi=0,int type=0){//_N表示数值  Wi表示位置 
		val=n[_N];
		des=type*pow(10,Wi); 
	}
}a[2000];
bool check(num *t,int L){//检查 
	int num=0;
	for(int i=1;i<=L;i++){
		if(!t[i].check())return false;
		num+=t[i].des*t[i].get();
	}
	return num==0;
}
int tot=0;
signed main(){
	//freopen("t.in","r",stdin);
	int len=0,eq=1;
	while(true){
		ch[++len]=getchar();
		if(ch[len]=='#')break;
	}
	while(ch[eq]!='=')eq++;
	//分别处理等号前后
	//把右边的等价到左边
	for(int i=len-1,j;i>eq;i=j-1){
		j=i;
		while(j-1>0&&isdigit(ch[j-1]))j--;
		int type=-1;
		if(ch[j-1]=='-')type=1;
		for(int w=i;w>=j;w--)
			a[++tot]=num(ch[w]-'0',i-w,type);
		if(ch[j-1]=='+'||ch[j-1]=='-')j--;
	} 
	for(int i=eq-1,j;i>=1;i=j-1){
		j=i;
		while(j-1>0&&isdigit(ch[j-1]))j--;
		int type=1;
		if(ch[j-1]=='-')type=-1;
		for(int w=i;w>=j;w--)
			a[++tot]=num(ch[w]-'0',i-w,type);
		if(ch[j-1]=='+'||ch[j-1]=='-')j--;
	} 
	//for(int i=1;i<=tot;i++)
	//	printf("%d*%d ",a[i].get(),a[i].des);
	check(a,tot);
	for(int i=1;i<=tot;i++)
		for(int j=0;j<8;j++)//枚举拿走的火柴
			if(a[i].check(j))
				for(int w=1;w<=tot;w++)
					for(int k=0;k<8;k++)
						if(!a[w].check(k)){
							//将i的j放到w的k上
							a[i].change(j);
							a[w].change(k);
							if(check(a,tot)){
								int p=tot;
								for(int i=1;i<=len;i++)
									if(isdigit(ch[i]))putchar(a[p--].get()+'0');
									else putchar(ch[i]);
								return 0;
							} 
							a[i].change(j);
							a[w].change(k);
						}
	printf("No"); 
	return 0;
}

 在百忙之中写一篇题解也比较辛苦，别忘了点个赞！