求解最优化问题时候通常要经过一串步骤,每一步都有多种选择。对于很多问题来说,用动态规划求最优解就是杀鸡用牛刀,可以使用更简单的算法。
贪心算法(greedy algorithm)在每一步都做出当时看起来是最佳的选择。也就是说,它综述做出局部最优的选择,希望通过局部最优解得到全局最优解。
贪心算法并不保证能得到最优解,但对于很多问题确实可以求得最优解。
16.1节将介绍活动选择问题(activity-selection problem)。16.2节将介绍贪心算法的基本原理。16.3节将介绍贪心算法的应用:设计一种数据压缩编码,即**哈夫曼(Huffman)**编码。
16.1 活动选择问题
假设有一个 nnn 个活动的集合 S={a1,a2,⋯ ,an}S=\{a_1, a_2, \cdots, a_n\}S={a1,a2,⋯,an},这些活动使用同一个资源(例如一个阶梯教室),而这个资源在某个时刻只能供一个活动使用。每个活动 aia_iai 都有一个开始时间 sis_isi 和一个结束时间 fif_ifi,其中 0≤si<fi<∞0 \le s_i \lt f_i \lt \infty0≤si<fi<∞。如果被选中,任务 aia_iai 发生在半开时间区间 [si,fi][s_i, f_i][si,fi] 期间。如果两个活动 aia_iai 和 aja_jaj 满足 [si,fi)[s_i, f_i)[si,fi) 和 [sj,fj)[s_j, f_j)[sj,fj) 不重叠,则称它们是兼容的。也就是说,若 si≥fjs_i \ge f_jsi≥fj 或 sj≥fis_j \ge f_isj≥fi,则 aia_iai 和 aja_jaj 是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动子集。假定活动已按结束时间的单调递增顺序排序:
f1≤f2≤f3≤⋯≤fn
f_1 \le f_2 \le f_3 \le \cdots \le f_n
f1≤f2≤f3≤⋯≤fn
例如,考虑下面的活动集合 SSS:
| iii | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| sis_isi | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 8 | 8 | 2 | 12 |
| fif_ifi | 4 | 5 | 6 | 7 | 9 | 9 | 10 | 11 | 12 | 14 | 16 |
子集 {a3,a9,a11}\{a_3, a_9, a_{11}\}{a3,a9,a11} 由相互兼容的活动组成。但它不是一个最大兼容活动子集。实际上,{a1,a4,a8,a11}\{a_1, a_4, a_8, a_{11}\}{a1,a4,a8,a11} 是一个最大兼容活动子集,另一个最大兼容活动子集是{a2,a4,a9,a11}\{a_2, a_4, a_9, a_{11}\}{a2,a4,a9,a11}。
活动选择问题的最优子结构
最优子结构是指一个问题具有递归结构,并且原问题的最优解可以通过一系列子问题的最优解来构建得到。换句话说,如果一个问题的最优解可以通过其子问题的最优解来推导得出,那么这个问题就具有最优子结构。
最优子结构是动态规划算法中的一个关键概念。在使用动态规划解决问题时,我们将问题划分为若干个子问题,并通过递归地解决子问题来获得原问题的最优解。通过最优子结构的特性,我们可以在求解子问题时将其最优解进行存储,以便后续的计算和使用。
通过将问题划分为子问题,并利用最优子结构的特性,动态规划算法能够避免重复计算,提高效率,并且能够在多项式时间内求解复杂的问题。因此,最优子结构是动态规划算法的一个重要性质,对于设计和分析动态规划算法非常关键。
令 SijS_{ij}Sij 表示在 aia_iai 结束之后开始,在 aja_jaj 开始之前结束的那些活动的集合。假设我们希望求 SijS_{ij}Sij 的一个最大兼容活动子集,进一步假设 AijA_{ij}Aij 就是这样一个子集,包含活动 aka_kak。由于最优解包含活动 aka_kak,我们得到两个子问题:寻找 SikS_{ik}Sik 中的兼容活动(在 aia_iai 结束之后开始且在 aka_kak开始之前结束的活动)以及寻找 SkjS_{kj}Skj 中的兼容活动(在 aka_kak 结束之后开始且在 aja_jaj开始之前结束的活动)。令 Aik=Aij⋂SikA_{ik}=A_{ij} \bigcap S_{ik}Aik=Aij⋂Sik 和 Akj=Aij⋂SkjA_{kj}=A_{ij} \bigcap S_{kj}Akj=Aij⋂Skj,这样 AikA_{ik}Aik 中包含 AijA_{ij}Aij 中哪些在 aka_kak 开始之前结束的活动,AkjA_{kj}Akj 包含 AijA_{ij}Aij 中哪些在 aka_kak 结束之后开始的活动。
因此,可以得到 Aij=Aik⋃{ak}⋃AkjA_{ij}=A_{ik} \bigcup \{a_k\} \bigcup A_{kj}Aij=Aik⋃{ak}⋃Akj,而且 SijS_{ij}Sij 中的最大兼容活动子集 AijA_{ij}Aij 包含 ∣Aij∣=∣Aik∣+∣Akj∣+1|A_{ij}|=|A_{ik}| + |A_{kj}| + 1∣Aij∣=∣Aik∣+∣Akj∣+1 个活动。
这样刻画活动选择问题的最优子结构,意味着我们可以用动态规划方法求解活动选择问题。如果用 c[i,j]c[i, j]c[i,j] 表示集合 SijS_{ij}Sij 的最优解大小,则可得递归式
c[i,j]=c[i,k]+c[k,j]+1
c[i, j]=c[i,k]+c[k,j]+1
c[i,j]=c[i,k]+c[k,j]+1
当然,如果不知道 SijS_{ij}Sij 的最优解包含活动 aka_kak,就需要考察 SijS_{ij}Sij 中的所有活动,寻找哪个活动可获得最优解,于是
c[i,j]={0若Sij=∅maxak∈Sij(c[i,k]+c[k,j]+1)若Sij≠∅
c[i, j]=\begin{cases}
0 &\text{若}S_{ij}=\varnothing \\
max_{a_k \in S_{ij}}(c[i, k]+c[k, j]+1) &\text{若}S_{ij} \ne \varnothing\end{cases}
c[i,j]={0maxak∈Sij(c[i,k]+c[k,j]+1)若Sij=∅若Sij=∅
贪心选择
贪心选择一个能够尽早结束活动,这样留下尽可能多的资源供接下来的活动使用。
定理:考虑任意非空子问题 SkS_kSk ,如果 ama_mam 是 SkS_kSk 中结束时间最早的活动,那么 ama_mam 在 SkS_kSk 的某个最大兼容活动子集中。
我们每次选择结束时间最早的且与当前活动兼容的活动,重复执行这个过程直到没有剩余活动可以选择。所选择的活动的结束时间必然是严格递增的。所以我们只需要按照结束时间单调递增的顺序处理所有活动,每个活动仅需要考察一次。
求解活动选择问题的算法不必像基于表格的动态规划算法那样自底向上进行计算。相反,可以自顶向下进行计算,选择一个活动放入最优解,然后,对剩余的子问题进行求解。贪心算法通常都是这种自顶向下的设计:做出一个当前最优的选择,然后求解剩下的子问题,而不是自底向上低求解出很多子问题,然后再做出选择。
递归贪心算法
RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
m = k + 1
while m ≤ n and s[m] < f[k] // find the first activity in S_k to finish
m = m + 1
if m ≤ n
return {a_m} ∪ RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)
else return ∅
RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) // call function

迭代贪心算法
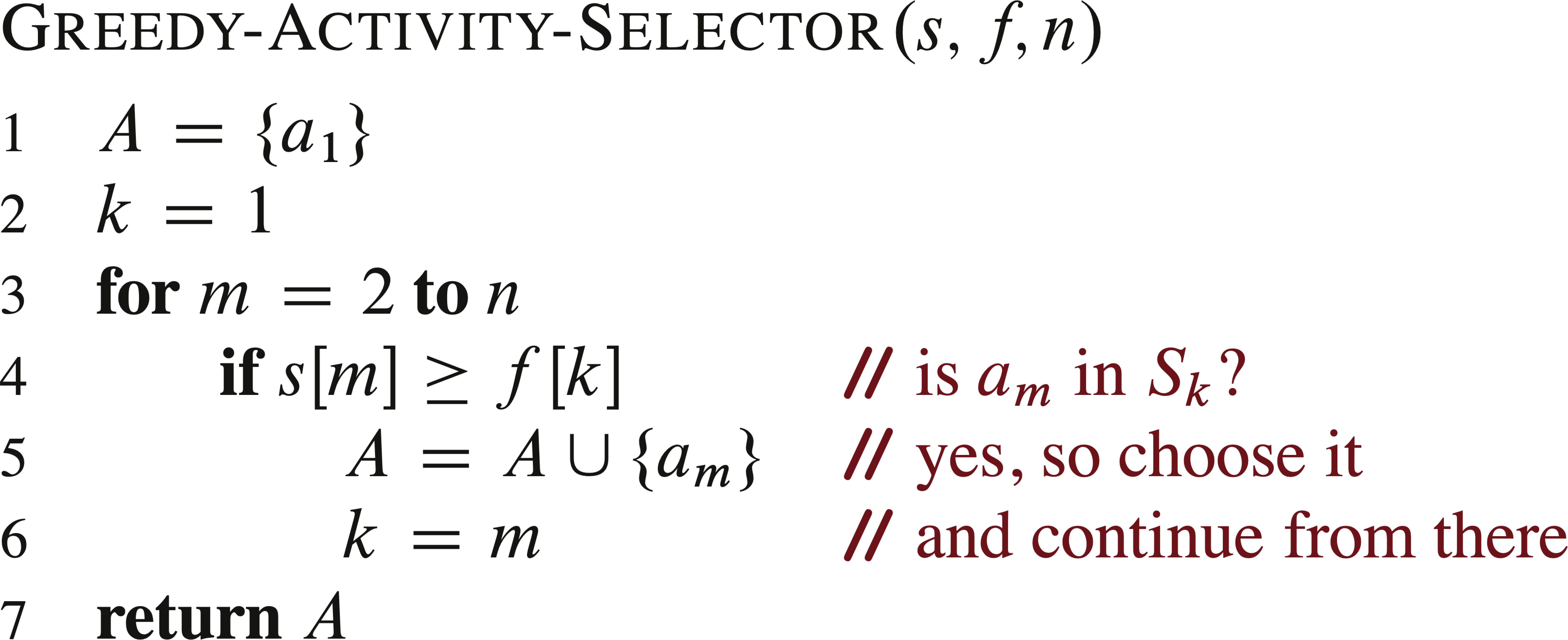
变量 kkk 记录了最近加入集合 AAA 的活动下标,对应递归算法中的活动 aka_kak ,由于我们按照结束时间单调递增处理活动。 fkf_kfk 是 AAA 中活动的的最大结束时间,也就是说,
fk=max{fi:ai∈A}
f_k=max\{f_i:a_i \in A\}
fk=max{fi:ai∈A}
与递归版本类似,在输入活动已按结束时间排序的前提下,GREEDY-ACTIVITY-SELECTOR的运行时间为 Θ(n)\Theta(n)Θ(n)。
16.2 贪心算法原理
一般情况下,我们可以根据以下步骤设计贪心算法。
- 最优化问题为你做出选择后只有一个子问题需要求解。
- 证明每次做出贪心选择后,原问题总是有最优解,所以贪心选择总是安全的。
- 证明做出贪心选择后的子问题和贪心选择一起构成原问题的最优解,即原问题具有最优子结构。
能够用贪心算法求解的问题具有贪心选择性质和最优子结构。
贪心选择性质(Greedy-choice property)
贪心选择性质:可以通过作出局部最优(贪心)选择来构造全局最优解。
贪心算法和动态规划的对比:
- 动态规划的选择依赖于子问题的解,所以一般采用自底向的方法求解问题。
- 贪心算法不依赖于子问题的解,所以一般采用自顶向下的方法求解问题。
使用贪心算法前,我们必须证明每个步骤做出贪心选择能生成全局最优解。
如果我们进行贪心选择时不得不考虑众多选择,我们必须提高进行贪心选择的效率。通过对输入数据进行**预处理(preprocess)**或者选择合适的数据结构(通常是优先队列),我们可以快速做出贪心选择,从而得到高效的算法。
最优子结构(Optimal substructure)
最优子结构(optimal substructure):如果一个问题的最优解包含其子问题的最优解,那么称该问题具有最优子结构。
贪心算法通常采用一个非常直接的方法运用最优子结构,假定通过对原问题的贪心选择就可以得到子问题,我们只需要证明做出贪心选择后的子问题和贪心选择一起构成原问题的最优解。该方法隐式地运用了归纳法,证明了每一步贪心选择都能构成原问题的最优解。
贪心VS动态规划(Greedy versus dynamic programming)
虽然贪心和动态规划方法都对问题的最优子结构进行了研究,但是如何选择两种方法求解问题却是个难点,所以我们用下面两个问题进行举例。
-
0-1背包问题(0-1 knapsack problem):商店里有 nnn 个商品,第 iii 个商品的价值为 viv_ivi,重量为 wiw_iwi,现在有一个可容纳最大重量为 WWW 的背包,目标使得背包中的商品价值最大,对于每个商品要么完整的拿走,要么留下,而不能只拿走一部分。
-
分数背包问题(fractional knapsack problem):问题场景和0-1背包问题一样,唯一区别是可以选择拿走商品的一部分,应该选择哪些商品。
两个**背包问题(knapsack problem)**都具有最优子结构。分数背包问题可以用贪心策略求解。0-1背包问题只能用动态规划求解。
16.3 赫夫曼编码
赫夫曼编码(Huffman codes)可以有效的压缩数据:通常可以节省20%~90%的空间,具体压缩效率依赖数据的特性。
每个字符用一个唯一的二进制串表示,称为码字。
假设我们希望压缩一个10万个字符的数据文件。下表给出了文件中出现的字符及其出现频率。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 频率(千次) | 45 | 13 | 12 | 16 | 9 | 5 |
| 定长编码 | 000 | 001 | 011 | 011 | 100 | 101 |
| 变长编码 | 0 | 101 | 100 | 111 | 1101 | 1100 |
-
定长编码(fixed-length code):所有字符的码字长度相同,需要使用 ⌈logn⌉\lceil \log n \rceil⌈logn⌉ 个比特位表示 n≥2n≥2n≥2 个字符。
-
变长编码(variable-length code):高频字符使用短码字,低频字符使用长码字。
前缀码(prefix code):没有任何码字是其他码字的前缀。前缀码的作用是简化解码过程。由于没有码字是其他码字的前缀,编码文件的开始码字是无歧义的。我们可以简单地识别出开始码字,将其转换回原字符,然后对编码文件剩余部分重复这种解码过程。在上面的例子中,二进制串 001011101 可以唯一地解析为 0 0 101 1101,解码为aabe。
一种二叉树可以满足这种需求,其叶结点为给定的字符。字符的二进制码用从根结点到叶结点的简单路径表示,其中0意味着转向左子树,1意味着转向右孩子。注意,这样得到的编码树并不是二叉搜索树,因为叶结点并未按照二叉搜素树有序排列。下图展示了字符集的两种编码方式:

文件的最优编码可以用一棵满二叉树表示,即每个非叶结点都有两个孩子结点。因此,对于字符集 CCC,最优前缀码对应的二叉树中有 ∣C∣|C|∣C∣ 个叶结点,每个叶结点对应一个字符,且有 ∣C∣−1|C|-1∣C∣−1 个内部结点。
给定一棵对应前缀码的树 TTT,字符集 CCC 中每个字符 ccc 出现的频率为 c.freqc.freqc.freq,令 dT(c)d_T(c)dT(c) 表示 ccc 的叶结点在树中的深度。dT(c)d_T(c)dT(c) 也是字符 ccc 的码字的长度。则编码文件需要
B(T)=∑c∈Cc∗freq∗dT(c)
B(T)=\sum_{c \in C} c * freq * d_T(c)
B(T)=c∈C∑c∗freq∗dT(c)
个二进制位,B(T)B(T)B(T) 为代价。
构造赫夫曼编码
赫夫曼设计了一个贪心算法来构造最优前缀码,被称为赫夫曼编码(Huffman code)。
算法思想:假定 CCC 是一个 nnn 个字符的集合,其中 c∈Cc \in Cc∈C 都是一个字符对象,其属性 c.freqc.freqc.freq 给出了字符出现的频率。算法自底向上地构造出对应最优编码的二叉树 TTT。它从 ∣C∣|C|∣C∣ 个叶结点开始,执行 ∣C∣−1|C|-1∣C∣−1个“合并”操作创建出最终的二叉树。算法使用一个以 freqfreqfreq 为关键字的最小优先队列 QQQ,用以识别两个最低频率的字符将其合并。当合并两个字符对象时,得到的新对象的频率设置为原来两个对象的频率之和。
HUFFMAN(C)
n = |C|
Q = C
for i = 1 to n - 1
allocate a new node z
x = EXTRACT-MIN(PQ)
y = EXTRACT-MIN(PQ)
z.left = x
z.right = y
z.freq = x.freq + y.freq
INSERT(PQ, z)
return EXTRACT-MIN(PQ) // the root of the tree is the only node left

需要合并 n−1n-1n−1 次,每次优先队列调整的运行时间为 O(logn)\Omicron(\log n)O(logn) ,所以HUFFMAN的运行时间为 O(nlogn)\Omicron(n\log n)O(nlogn)。
读取文件,编程实现Huffman编码问题,输出编码方案和压缩率。
import java.io.*;
import java.text.DecimalFormat;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class HuffmanNode implements Comparable<HuffmanNode> {
Character character;
Integer freq; // 频率
HuffmanNode left; // 左子树
HuffmanNode right; // 右子树
public HuffmanNode(Character character, Integer freq, HuffmanNode left, HuffmanNode right) {
this.character = character;
this.freq = freq;
this.left = left;
this.right = right;
}
public boolean isLeaf() {
return left == null && right == null;
}
@Override
public int compareTo(HuffmanNode o) {
return freq - o.freq;
}
}
public class HuffmanCode {
/**
* 读取指定路径的文件,统计文件内字符及其出现的频率
* @param filePath 文件路径
* @return 哈希表
*/
public static HashMap<Character, Integer> countFreq(String filePath) {
HashMap<Character, Integer> frequencyMap = new HashMap<>();
try {
BufferedReader reader = new BufferedReader(new FileReader(filePath));
int c;
while ((c = reader.read()) != -1) {
char character = (char) c;
// 忽略空格和换行符
if (!Character.isWhitespace(character) && character != '\n') {
frequencyMap.put(character, frequencyMap.getOrDefault(character, 0) + 1);
}
}
//// 打印字符及其频率
//for (Map.Entry<Character, Integer> entry : frequencyMap.entrySet()) {
// System.out.println(entry.getKey() + ": " + entry.getValue());
//}
} catch (IOException e) {
e.printStackTrace();
}
return frequencyMap;
}
/**
* 构造Huffman编码树
* @param hashMap <字符,频率>哈希表
* @return HuffmanNode
*/
public static HuffmanNode buildHuffmanTree(HashMap<Character, Integer> hashMap) {
PriorityQueue<HuffmanNode> priorityQueue = new PriorityQueue<>();
for (Map.Entry<Character, Integer> entry : hashMap.entrySet()) {
priorityQueue.offer(new HuffmanNode(entry.getKey(), entry.getValue(), null, null));
}
while (priorityQueue.size() > 1) {
HuffmanNode z = new HuffmanNode('\0', 0, null, null);
HuffmanNode left = priorityQueue.poll();
HuffmanNode right = priorityQueue.poll();
z.left = left;
z.right = right;
z.freq = left.freq + right.freq;
priorityQueue.offer(z);
}
return priorityQueue.poll();
}
/**
* 生成Huffman编码
* @param huffmanNode Huffman结点
* @return HashMap<Character, String>
*/
public static HashMap<Character, String> generateHuffmanCode(HuffmanNode huffmanNode) {
HashMap<Character, String> huffmanCodes = new HashMap<>();
generateHuffmanCodeHelper(huffmanNode, "", huffmanCodes);
return huffmanCodes;
}
public static void generateHuffmanCodeHelper(HuffmanNode node, String code, HashMap<Character, String> huffmanCodes) {
if (node == null) {
return;
}
if (node.isLeaf()) {
huffmanCodes.put(node.character, code);
}
generateHuffmanCodeHelper(node.left, code + '0', huffmanCodes);
generateHuffmanCodeHelper(node.right, code + '1', huffmanCodes);
}
/**
* 输出文件
* @param pathRes 文件路径
* @param hashMap hashMap
* @param huffmanCodes huffmanCodes
* @throws IOException
*/
public static void output(String pathRes, HashMap<Character, Integer> hashMap, HashMap<Character, String> huffmanCodes) throws IOException {
FileWriter fileWriter = null;
BufferedWriter bufferedWriter = null;
try {
File file = new File(pathRes);
if (!file.exists()) {
file.createNewFile();
}
fileWriter = new FileWriter(file);
bufferedWriter = new BufferedWriter(fileWriter);
StringBuilder stringBuilder = new StringBuilder();
stringBuilder.append("字符").append("\t\t\t").append("出现频率").append("\t\t\t").append("编码").append("\n");
for (Map.Entry<Character, Integer> entry : hashMap.entrySet()) {
if (huffmanCodes.containsKey(entry.getKey())) {
String code = huffmanCodes.get(entry.getKey());
stringBuilder.append(entry.getKey()).append("\t\t\t").append(entry.getValue()).append("\t\t\t").append(code).append("\n");
}
}
bufferedWriter.write(stringBuilder.toString());
} catch (IOException e) {
e.printStackTrace();
} finally {
bufferedWriter.close();
}
}
/**
* 计算压缩率
* @param hashMap hashMap
* @param huffmanCodes huffmanCodes
* @return double
*/
public static double computeCompressibility(HashMap<Character, Integer> hashMap, HashMap<Character, String> huffmanCodes) {
// 1、计算定长编码需要的空间
int cost1 = 0;
int size1 = hashMap.size();
int bits = (int) Math.ceil(Math.log(size1) / Math.log(2));
for (Map.Entry<Character, Integer> entry : hashMap.entrySet()) {
cost1 += bits * entry.getValue();
}
// 2、计算Huffman编码需要的空间
int cost2 = 0;
for (Map.Entry<Character, String> entry : huffmanCodes.entrySet()) {
int freq = hashMap.get(entry.getKey());
cost2 += entry.getValue().length() * freq;
}
return (double) cost2 / cost1;
}
public static void main(String[] args) throws IOException {
HashMap<Character, Integer> hashMap = countFreq("C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch16\\orignal.txt");
System.out.println(hashMap);
HashMap<Character, String> huffmanCodes = generateHuffmanCode(buildHuffmanTree(hashMap));
output("C:\\Projects\\IDEAProjects\\algorithms\\src\\main\\java\\ch16\\table.txt", hashMap, huffmanCodes);
double compressibility = computeCompressibility(hashMap, huffmanCodes);
DecimalFormat df = new DecimalFormat("0.00%");
String res = df.format(compressibility);
System.out.println("压缩率: " + res);
}
}
参考
- https://zhuanlan.zhihu.com/p/573336677
- 《算法导论》第3版 中文版





















 1023
1023

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








