有很多文章讨论在scratch中画圆的方法,所看到的文章中有如下方法:多边形逼近法、图章法、克隆法、三角函数法、方程遍历法、圆的标准方程法等。对于多边形逼近法,所看到文章都认为其缺点是很难精准的控制圆的半径和圆心的位置,感觉这种看法有些片面。首先看下面的脚本,使用360个边的多边形逼近圆,每边对应1度圆心角,边长为2,该圆圆心在(0,0),半径为114.6。见下图。
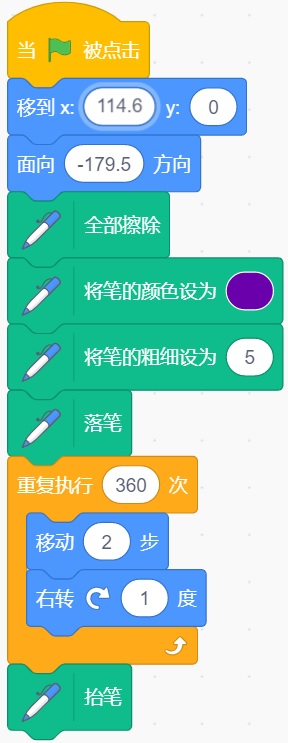
所画圆的半径是可以计算出来的。弧度定义:弧长/半径。所以360度角度所对应的弧度为2πr/r=2π,1度角度用弧度表示为2π/360,即近似为1/57.29578。所画圆1度圆心角对应的弧长近似为360个边的多边形的边长(为2),根据定义,1度角度所对应弧度1/57.29578=边长2/半径,则半径为57.29578*2= 114.59156。有了半径,就可以画指定圆心位置和半径的圆,例如圆心坐标为(x,y),半径为r,将画园起点移动到(x+r,y),即可画指定圆心和半径的园。以上脚本第1条语句“移到x:114.6 Y:0”,将圆心坐标设定为(0,0),圆的半径为114.6。第2条语句是设定第1条边的方向。运行效果图如下。请注意,铅笔的定位点在笔尖上,见下边右图。
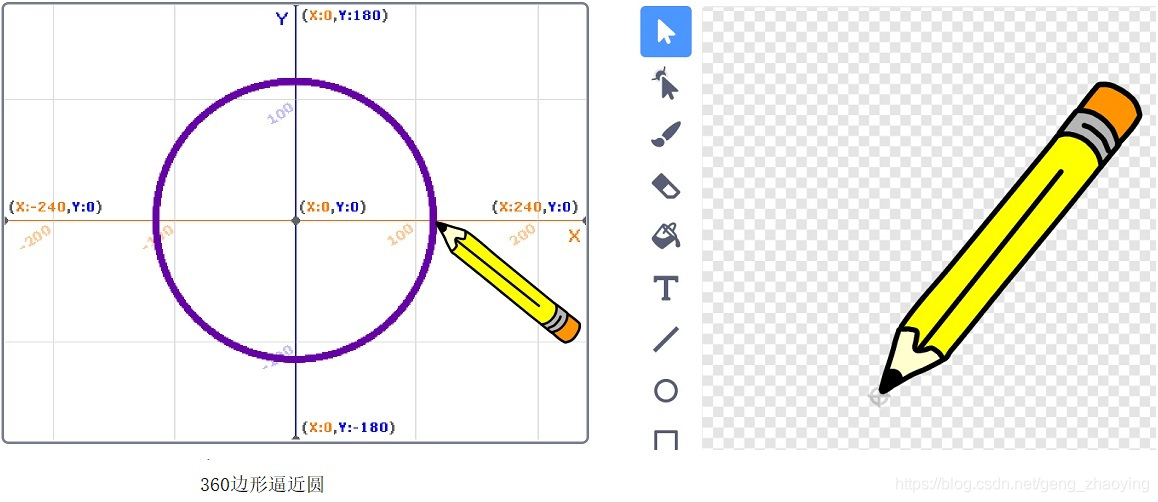
应注意到,用360个边的多边形逼近圆,画圆的速度太慢了。在scratch中画圆,逼近圆的多边形的边长在15以下,就能画出比较满意的圆。可修改上边脚本:循环次数=48,每次右转7.5度,移动15步,看一看是否满意,速度快多了。见下图。
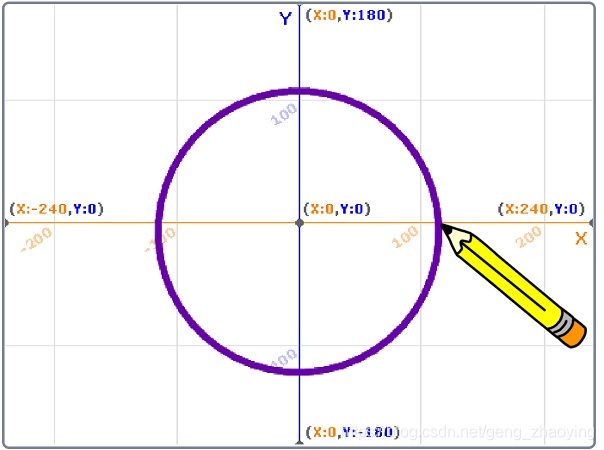
但有一个问题,圆心不在坐标原点上。这是由于设定第1条边的方向不正确。下边讨论如何得到第1条边的方向。为了直观,画出了用5、6和8条边的多边形逼近圆的图形。见下图。
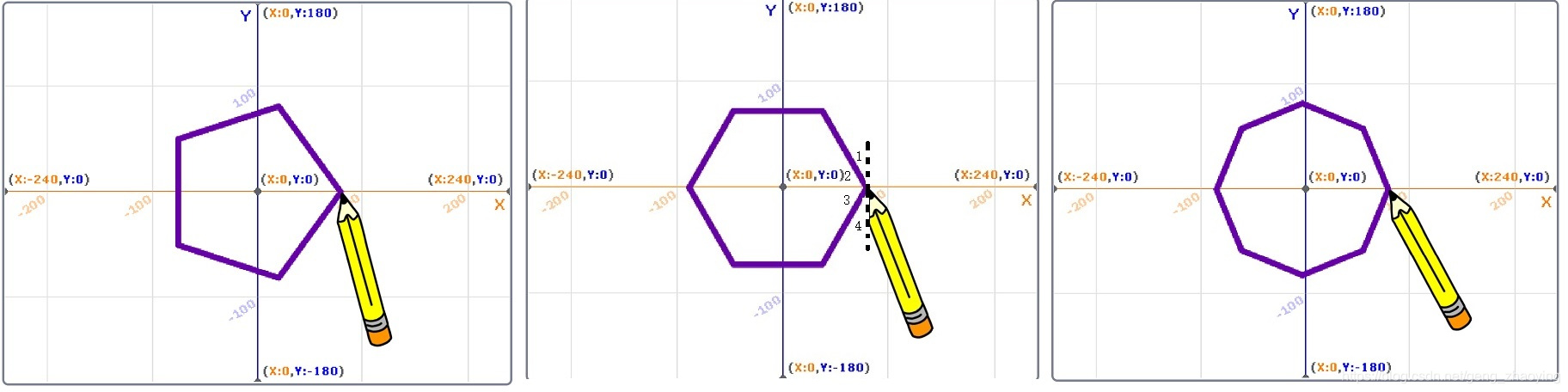
这些图形都以x坐标轴为对称轴,以6边形为例,见上图,角1=角4,角2=角3,角2+角3=120度,则角4=30度,因此所画6边形的第1条边的方向为-150度,画6边形程序的第2条语句要改为“面向-150方向”。总结计算公式为:第一条边起始方向=-180+(右转角度/2)。在实际使用中,首先知道圆心位置和圆的半径,计算出周长,除以15,得出循环大概次数,调整循环次数使其能被360整除,得到循环次数,360度/循环次数得到每次右转的角度,然后用周长除以循环次数,得到每次移动步数。设定圆点坐标为:(0,0),半径=80,下边表中列出几种多边形逼近圆所需参数。
几边形 半径 起始方向 起点坐标 循环次数 右转角度 移动步数
5边形 8 0 -144 ( 8 0 , 0 ) 5 7 2 100.53
6边形 80 - 150 ( 8 0 , 0 ) 6 6 0 83.78
8边形 80 - 157.5 ( 8 0 , 0 ) 8 4 5 62.83
36边形 80 - 175 ( 8 0 , 0 ) 36 1 0 13.96
45边形 80 - 176 ( 8 0 , 0 ) 45 8 11.17
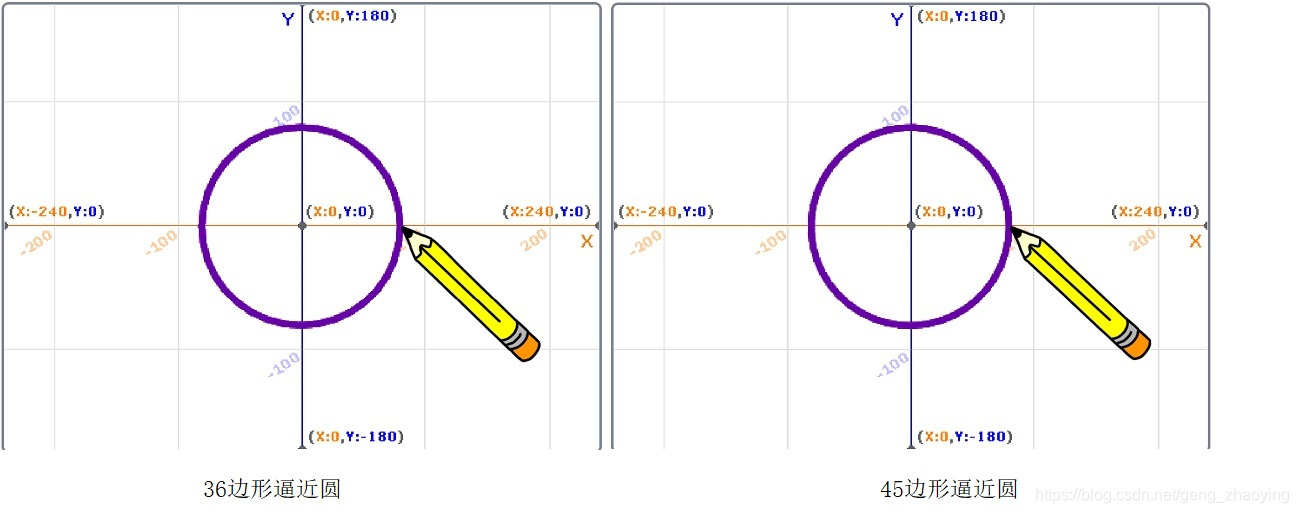
按表中参数,用36边形和45边形画圆所得图形见下图。可见两者所画的圆区别不大。
在scratch中用多边形逼近法和弧度概念画指定圆心和半径的圆
最新推荐文章于 2024-11-24 11:23:54 发布
 本文探讨了在Scratch中使用多边形逼近法画圆的多种参数设置,通过调整边数、方向和步长,实现了快速且精确的圆绘制,同时提供了不同边数下画圆的具体参数。
本文探讨了在Scratch中使用多边形逼近法画圆的多种参数设置,通过调整边数、方向和步长,实现了快速且精确的圆绘制,同时提供了不同边数下画圆的具体参数。





















 766
766

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








