图的储存（邻接矩阵、邻接表，邻接多重表，简洁实用版有向邻接多重表）

一、邻接矩阵

对于邻接矩阵，比较的简单好理解。由于对于稀疏图来讲这种算法太过于浪费空间，一般情况下也不采用这种方法进行图的储存，但是由于可以帮助理解图的特点，这里就简单的介绍一下。

邻接矩阵存储结构用于表示顶点之间的相邻关系，其中通过一个一维数组存储顶点，一个二维数组存储顶点之间的相邻关系，一个顶点数为n的图的邻接矩阵是n×n（n行n列），即一个方阵，用邻接矩阵方法来表示一个图需要个存储空间。二维数组a[i][j]代表 i 点到 j 点的边。如果a[i][j]=0则代表i j 之间不相连，对于不带权的图a[i][j]=1代表i j 相连。对于带权的图a[i][j]=k代表i j 之间的权为k。

不带权的图 ：

 邻接矩阵有以下几个性质：

1.由于邻接矩阵是方阵，所以图的顶点数等于邻接矩阵的行或列的数目。

2.无向图的邻接矩阵一定是对称矩阵，关于对角线对称，且主对角线一定为零（只针对简单图），而有向图的邻接矩阵不一定是对称矩阵。

代码实现：

自己实现吧（哈哈哈

二、邻接表

邻接表方法采用顺序存储结构和链式存储结构来存储图

简单讲就是有两个表，一个是顶点表，一个是边表。顶点表中除了数据域用于存储顶点信息，还有指向第一条与其邻接顶点的指针域；边表中由邻接点域和指向下一条邻接边的指针域组成。（这个边表不是另外一个表，是指跟在数组后面的一串链）

无向图的邻接表

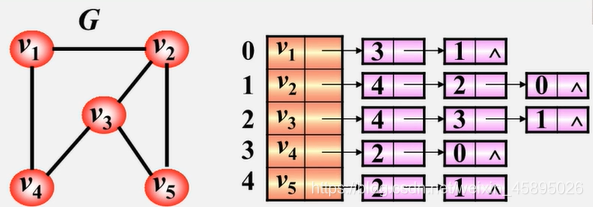
有向图的邻接表

 由这两个图就可以很清楚的知道邻接表的链上代表的就是下一个点的id编号。

代码实现：

思路很清晰，首先一个结构体代表顶点表v[maxn]，里面val代表边权，id代表编号，next代表该点连接的第一个边的点的指针。之后如果发现v还连接其他点就和链表的创建一样，连在next后面。接下来详细的解释在代码里，如果有哪里有疑问可以留言。

#include<iostream>
using namespace std;
const int maxn=1e3;
int cin_g[maxn][maxn];//输入样例是一个邻接矩阵，在代码结尾
int n;//n个点

struct node{
	node *next;
	int val;
	int id;
}v[maxn];//顶点表
int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
	{
		v[i].next=NULL;//初始顶点表不与任何点相连
		for(int j=0;j<n;j++)
		{
			cin>>cin_g[i][j];//输入样例
		}
	}
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			if(cin_g[i][j]>0)//如果i j 相连
			{
				node* va=new node;//创建一个顶点的指针（边表）
				va->val=cin_g[i][j];
				va->next=NULL;
				va->id=j;
				if(!v[i].next)v[i].next=va;//如果i还没有与之相连的点，直接连在i后面
				else//如果有，找到最后一个相连的点，接在他后面
				{
					node* p=new node;
					p=v[i].next;
					while(p)
					{
						if(!p->next)
						{
							p->next=va;
							break;
						}
						else	p=p->next;
					}
				}
			}
		}
	}
	for(int i=0;i<n;i++)
	{
		node* pp=v[i].next;//用于遍历边表
		while(pp)
		{
			cout<<i<<"->"<<pp->id<<"权值是"<<pp->val<<" ";
			pp= pp->next;
		}
		cout<<endl;
	 } 
	return 0;
	
}

/*
3
1 0 1
5 2 0
4 5 6
*/

三、邻接多重表

简单的来说，对于一个有向图，也是通过顶点表和边表，将一条边的两个顶点存放在边表结点中，而将邻接于同一个顶点的边串联在顶点表结点中，即邻接多重表，它是邻接表的改进方法。

这种存储方式解决了邻接表在存储无向图时同一条边要存储两次的问题，即一条边只需一个结点来记录，避免了同一条边的重复存储，提高了空间存储效率。

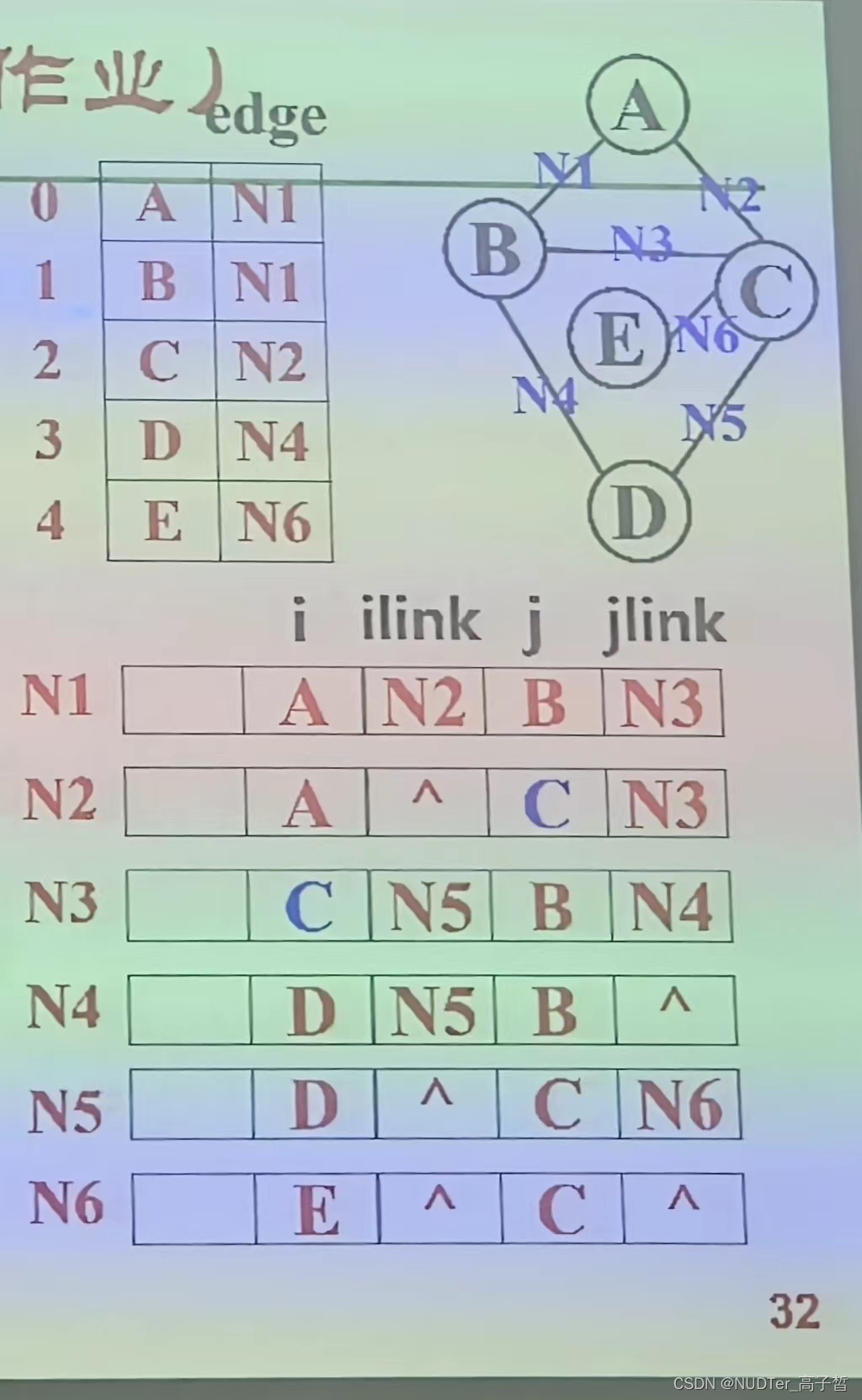
对着这个图来讲就是，这个边表是真的边表。储存着N1-N6的边，每个边的数据包括第一个空格子时mark 代表是否访问过，i 和 j 代表边左右相连的点，ilink 代表 i 之后连接的边，jlink 代表 j 之后连接的边。对于顶点表，分别记录所有的点和该点第一个与之相连的边。

这样就能将这个图穿起来，我演示下遍历这个图可能就更好理解为什么这么储存了。当我想要遍历A点的边，我先在顶点表中找到A，我就知道与A第一个相连的边是哪个，这个图里是N1（第一第二的顺序是按输入边来看的，顺序没关系的，随便找个就行）然后跳到边表找N1看A连的下一个边是谁，也就是ilink 这个图是N2，跳到N2 看A连接的下一个边是谁，一看没有了，就填空，结束。

代码实现：

#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>

using namespace std;
int n, m;
struct Edge {
	bool vis;
	char i;
	int ilink;
	char j;
	int jlink;
}edge[103];

struct Node {
	char dataa;
	int pos;
}node_firstpos[12];

void insert(char x, char y, int pos)
{
	edge[pos].vis = false;
	edge[pos].i = x;
	edge[pos].j = y;
	edge[pos].ilink = 0;
	edge[pos].jlink = 0;
	for (int i = 1; i <= n; i++)
	{
		if (node_firstpos[i].dataa == x || node_firstpos[i].dataa == y)
		{
			int tmp = node_firstpos[i].pos;
			int tmp_dataa = node_firstpos[i].dataa;
			if (tmp == 0)
			{
				node_firstpos[i].pos = pos;
			}
			else {
				int tm = 0;
				while (tmp != 0)
				{
					tm = tmp;
					if (edge[tmp].i == tmp_dataa)
					{
						tmp = edge[tmp].ilink;
					}
					else {
						tmp = edge[tmp].jlink;
					}
				}
				if (edge[tm].i == tmp_dataa)
				{
					edge[tm].ilink = pos;
				}
				else {
					edge[tm].jlink = pos;
				}
			}
		}
	}
}

void pri()
{
	for (int i = 1; i <= m; i++)
	{
		cout << edge[i].i << " " << edge[i].ilink << " " << edge[i].j << " " << edge[i].jlink << endl;
	}
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		char da;
		cin >> da;
		node_firstpos[i].dataa = da;
		node_firstpos[i].pos = 0;
	}
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		char x, y;
		cin >> x >> y;
		insert(x, y, i);
	}
	pri();
	return 0;
}

/*
5
A B C D E
6
A B
A C
C B
C E
D B
C D
*/

 这个代码实现比较复杂，我还不是很懂这个实现怎么应用到图论中，之后更新再解释吧。下面介绍一个简单版的。

四、简洁实用版有向邻接多重表

对于上面的邻接多重表，其实我们遍历的时候就知道这个似乎不需要储存那么多的信息，我只知道每个点在哪一个边，和那个边连接的那个点的下一个边是谁（对照邻接多重表）一直遍历下去，就找到了和这个点连接的所有的边，这也是邻接多重表的一个演化。

代码实现：

这个代码的精髓是由于边的顺序是没有关系的，我们记录边在那个边的时候，记录的是最后一个边，next记录的是前一个边，这样我们就可以一路递推就可以完成整个图的储存。

#include<iostream>
#define next nex
using namespace std;
const int maxn=1000001;
int first[maxn],next[maxn<<1],to[maxn<<1],val[maxn<<1],tot;
//tot是边的编号，next代表的是该点连接的下一个边，to代表该边连接的另一个点，val代表边权
int n,m;
void add(int x,int y,int z)
{
	next[++tot]=first[x];//该点连接的前一个边
	first[x]=tot;//点连接的最后一个边
	to[tot]=y;
	val[tot]=z;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y,1);
	}
	for(int e=first[2];e;e=next[e])//e从最后一个边开始，到e不为空，e下一个边是其前一个边
	{
		cout<<2<<"->"<<to[e]<<endl;
	}
	return 0;
}

/*
测试样例：
6 5
1 2 
2 3 
2 4 
2 5 
1 6
*/

参考博客：https://blog.youkuaiyun.com/qq_43085848/article/details/126315097