二叉树的基本性质（考点）

自学所用，不对之处望请斧正

参考连接：B站学习视频
考点一：
设非空二叉树中度为0、1和2的结点个数分别为n0、n1,和n2，则n0=n2+1(叶子结点比二分支结点多一个)
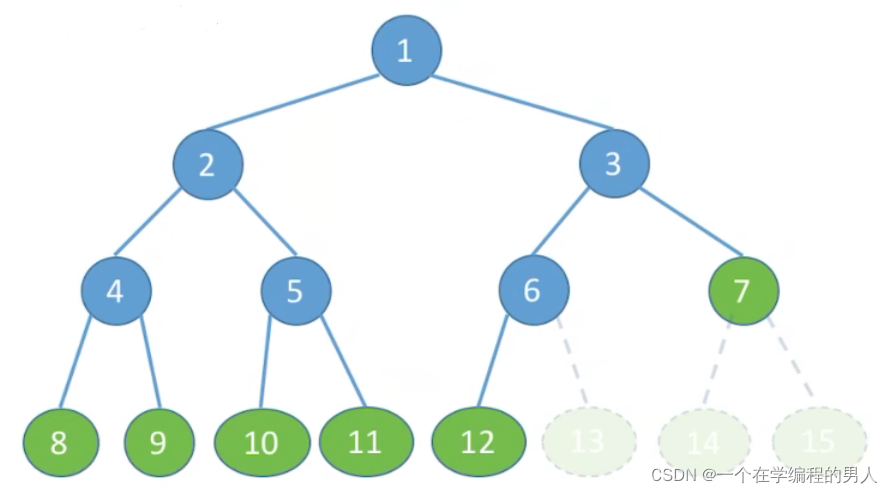
这个性质随便找个树都可以看的出来如下图

蓝色结点均为度为二的结点，数目为7；
绿色结点均为度为零的结点，数目为8；
绿色结点 = 蓝色结点 + 1；
注：此图并非个例

这个性质具体推导过程如下：
总结点个数 = n0 + n1 + n2;
总结点个数 = n0 * 0 + n1 * 1 + n2 * 2 + 1 = n1 + 2 * n2 + 1;
注：第一个式子是以结点本身相加得到，第二个式子是以各结点的孩子结点相加再加上根结点得到;
两式相减可得 n0 = n2 + 1;

考点二：
二叉树第i层至多有2的i - 1次方个结点
M叉树第i层至多有M的i - 1次方个结点

简单结论 看图即可！

考点三：
高度为h的二叉树至多有2的h次方-1个结点
此结论可由上图使用等比数列求和公式得到！

考点四：

第一个结论推导思想：高度为h的完全二叉树结点个数大于高度为h - 1的满二叉树，小于或等于高度为h的满二叉树。（参考点三结论）

第二个结论推导思想：度为h的完全二叉树结点个数大于或等于高度为h - 1的满二叉树 + 1，小于高度为h的满二叉树 + 1。

自己推 别死记

考点五：

因为 n = 2 * n2 + n1 + 1 且 完全二叉树中度为1的结点 只能有0或1个，(2 * n2 + 1 )必然为奇数；
所以可以通过判断n的奇偶来确定 n1 是 0 还是 1；
当n = 2k; n0 = k; n1 = 1; n2 = k - 1;
推导过程如下:
n1 = 1;
2k = 2 * n2 + n1 + 1;
2 * n2 + 1 = 2k - 1;
n2 = k - 1;
n0 = n2 + 1;
n0 = k;

当n = 2k - 1;n0 = k; n1 = 0; n2 = k - 1;
推导过程如下:
n1 = 0;
2k - 1 = 2 * n2 + 1;
n2 = k - 1;
n0 = n2 + 1;
n0 = k;

好家伙一顿推导 就 n1随着 n变呗就；

*完全二叉树的小性质： （用到过特别说明一下）
按层序从左向右标号 第i个结点的左孩子为 2i 右孩子 为 2i + 1 父结点为 [(int)i / 2];
[(int) n / 2]为分支结点 大于它的都是叶子结点；（n为总结点个数）
观察下图即可