hdu3507 Print Article

传送门
令$s[i]={\sum }_{i=1}^{n}C[i]$
有$DP$转移方程：
f [ i ] = m i n { f [ p ] + ( s [ i ] − s [ p ] ) 2 + m }         ( p ∈ [ 0 , i − 1 ] ) ) f[i]=min\{f[p]+(s[i]-s[p])^2+m\}\ \ \ \ \ \ \ (p∈[0,i-1])) f[i]=min{f[p]+(s[i]−s[p])2+m}       (p∈[0,i−1]))

令$0<=j<k<=i-1$。那么如果$j$的转移比$k$更优，那么有：
$$f[j]+(s[i]-s[j]{)}^2+m<f[k]+(s[i]-s[k]{)}^2+m$$

$$f[j]+s[i{]}^2+s[j{]}^2-2\ast s[i]\ast s[j]<f[k]+s[i{]}^2+s[k{]}^2-2\ast s[i]\ast s[k]$$

然后把只与$j$有关的挪到一块，把只与$k$有关的挪到一块。
$$(f[j]+s[j{]}^2)-(f[k]+s[k{]}^2)<2\ast s[i]\ast (s[j]-s[k])$$
令$T[i]=f[i]+s[i{]}^2$，于是有

$$T[j]-T[k]<2\ast s[i]\ast (s[j]-s[k])$$

由于$j<k$，于是$s[j]-s[k]<0$，那么有：
$$\frac{T[j]-T[k]}{s[j]-s[k]}>2\ast s[i]$$

这便是从$j$转移比从$k$转移更优的条件。
观察发现，左边的东西可以看做是斜率。$(k=\frac{\Delta y}{\Delta x})$
那么我们把每一个状态看做是一个点。第$i$个状态的坐标就是$(s[i],T[i])$。
求$f[i]$时，考虑从前$i$个点中最优的一个转移（包含坐标原点，即所有东西挤在一行）
令这个点为$j$。考虑任意一个$k$，满足$k>j$。
如果$jk$这条直线斜率比$2\ast s[i]$小，那么$k$就比$j$更优。这是不行的。

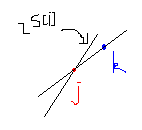
所以可以想象前面的$i$个状态在平面上对应出来一些点，一个斜率为$2\ast s[i]$的直线从下面无穷远处向上平移，它遇见的第一个点就是$f[i]$的最优转移。
显然，该直线遇见的第一个点一定在凸包上。可以用一个队列存储这些点。
然后有一个特点，就是$s[i]$是随着$i$增大而增大的。
也就是说，判断所用直线的斜率是单增的。
于是队列的左边界是单增的。
注意，队列里面存的是编号。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=5e5+10;
int head,tail,n,m,q[maxn];ll f[maxn],s[maxn];
inline int read(){
	int x=0;char ch=getchar();
	while(!isdigit(ch)) ch=getchar();
	while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
	return x;
}
inline ll calc(int i){return f[i]+s[i]*s[i];}
inline ll getx(int i,int j){return s[i]-s[j];}
inline ll gety(int i,int j){return calc(i)-calc(j);}
int main(){
	while(scanf("%d%d",&n,&m)!=EOF){
		head=tail=0;
		for(int i=1;i<=n;++i){
			s[i]=read()+s[i-1];
			while(head<tail&&gety(q[head+1],q[head])<=2*s[i]*getx(q[head+1],q[head])) head++;
			f[i]=f[q[head]]+(s[i]-s[q[head]])*(s[i]-s[q[head]])+m;
			while(head<tail&&((calc(i)-calc(q[tail]))*(s[q[tail]]-s[q[tail-1]])<=(calc(q[tail])-calc(q[tail-1]))*(s[i]-s[q[tail]]))) tail--;
			q[++tail]=i;
		}printf("%lld\n",f[n]);
	}
}