Mysql 的索引为什么使用 B+ 树而不使用跳表？

在我们的印象中，mysql数据表里无非就是存储一行行的数据。跟个excel似的。

直接遍历这一行行数据，性能就是O(n)，比较慢。为了加速查询，使用了B+树来做索引，将查询性能优化到了O(lg(n))。

但问题就来了，查询数据性能在 lg(n) 级别的数据结构有很多，比如redis的zset里用到的跳表，也是lg(n)，并且实现还贼简单。

那为什么mysql的索引，不使用跳表呢？

我们今天就来聊聊这个话题。

B+树的结构

我简单总结下B+树的结构。

B+树查询过程

如上图，一般B+树是由多个页组成的多层级结构，每个页16Kb，对于主键索引来说，最末级的叶子结点放行数据，非叶子结点放的则是索引信息（主键id和页号），用于加速查询。

比方说我们想要查找行数据5。会先从顶层页的record们入手。record里包含了主键id和页号（页地址）。关注黄色的箭头，向左最小id是1，向右最小id是7。那id=5的数据如果存在，那必定在左边箭头。于是顺着的record的页地址就到了6号数据页里，再判断id=5>4，所以肯定在右边的数据页里，于是加载105号数据页。

在105号数据页里，虽然有多行数据，但也不是挨个遍历的，数据页内还有个页目录的信息，它可以通过二分查找的方式加速查询行数据，于是找到id=5的数据行，完成查询。

从上面可以看出，B+树利用了空间换时间的方式（构造了一批非叶子结点用于存放索引信息），将查询时间复杂度从O(n)优化为O(lg(n))。

跳表的结构

看完B+树，我们再来看下跳表是怎么来的。

同样的，还是为了存储一行行的数据。

我们可以将它们用链表串起来。

单链表

想要查询链表中的其中一个结点，时间复杂度是O(n)，这谁顶得住，于是将部分链表结点提出来，再构建出一个新的链表。

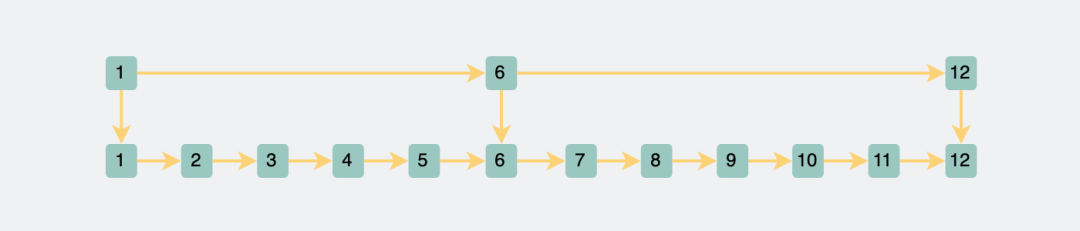
两层跳表

这样当我想要查询一个数据的时候，我先查上层的链表，就很容易知道数据落在哪个范围，然后跳到下一个层级里进行查询。这样就把搜索范围一下子缩小了一大半。

比如查询id=10的数据，我们先在上层遍历，依次判断1,6,12，很快就可以判断出10在6到12之间，然后往下一跳，就可以在遍历6,7,8,9,10之后，确定id=10的位置。直接将查询范围从原来的1到10，变成现在的1,6,7,8,9,10，算是砍半了。

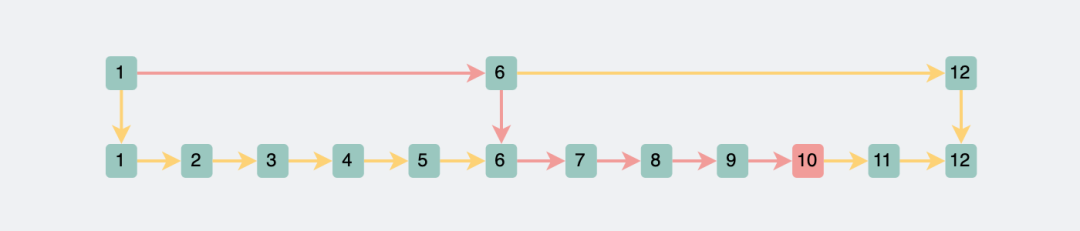
两层跳表查找id为10的数据

既然两层链表就直接将查询范围砍半了，那我多加几层，岂不妙哉？

于是跳表就这样变成了多层。

三层跳表

如果还是查询id=10的数据，就只需要查询1,6,9,10就能找到，比两层的时候更快一些。

三层跳表查询id为10的数据

可以看出，跳表也是通过牺牲空间换取时间的方式提升查询性能。时间复杂度都是lg(n)。

B+树和跳表的区别

从上面可以看到，B+树和跳表的最下面一层，都包含了所有的数据，且都是顺序的，适合用于范围查询。往上的层级都是构建出来用于提升搜索性能的。这两者实在是太像了。但他们两者在新增和删除数据时，还是有些区别的。下面我们以新增数据为例聊一下。

B+树新增数据会怎么样

B+树本质上是一种多叉平衡二叉树。关键在于"平衡"这两个字，对于多叉树结构来说，它的含义是子树们的高度层级尽量一致（一般最多差一个层级），这样在搜索的时候，不管是到哪个子树分支，搜索次数都差不了太多。

当数据库表不断插入新的数据时，为了维持B+树的平衡，B+树会不断分裂调整数据页。

我们知道B+树分为叶子结点和非叶子结点。

当插入一条数据时，叶子结点和它上层的索引结点（非叶子结点）最大容量都是16k，它们都有可能会满。

为了简化问题，我们假设一个数据页只能放三条行数据或索引。

加入一条数据，根据数据页会不会满，分为三种情况。

• 叶子结点和索引结点都没满。这种情况最简单，直接插入到叶子结点中就好了。

叶子和非叶子都未满

• 叶子结点满了，但索引结点没满。此时需要拆分叶子结点，同时索引结点要增加新的索引信息。

叶子满了但非叶子未满.drawio

• 叶子结点满了，且索引结点也满了。叶子和索引结点都要拆分，同时往上还要再加一层索引。

叶子和非叶子都满了

从上面可以看到，只有在叶子和索引结点都满了的情况下，B+树才会考虑加入一层新的结点。

而从之前的文章知道，要把三层B+树塞满，那大概需要2kw左右的数据。

跳表新增数据

跳表同样也是很多层，新增一个数据时，最底层的链表需要插入数据。

此时，是否需要在上面的几层中加入数据做索引呢？

这个就纯靠随机函数了。

理论上为了达到二分的效果，每一层的结点数需要是下一层结点数的二分之一。

也就是说现在有一个新的数据插入了，它有50%的概率需要在第二层加入索引，有25%的概率需要在第三层加个索引，以此类推，直到最顶层。

举个例子，如果跳表中插入数据id=6，且随机函数返回第三层（有25%的概率），那就需要在跳表的最底层到第三层都插入数据。

跳表插入数据

如果这个随机函数设计成上面这样，当数据量样本足够大的时候，数据的分布就符合我们理想中的"二分"。

跟上面B+树不一样，跳表是否新增层数，纯粹靠随机函数，根本不关心前后上下结点。

好了，基础科普也结束了，我们可以进入正题了。

Mysql的索引为什么使用B+树而不使用跳表？

B+树是多叉树结构，每个结点都是一个16k的数据页，能存放较多索引信息，所以扇出很高。三层左右就可以存储2kw左右的数据（知道结论就行，想知道原因可以看之前的文章）。也就是说查询一次数据，如果这些数据页都在磁盘里，那么最多需要查询三次磁盘IO。

跳表是链表结构，一条数据一个结点，如果最底层要存放2kw数据，且每次查询都要能达到二分查找的效果，2kw大概在2的24次方左右，所以，跳表大概高度在24层左右。最坏情况下，这24层数据会分散在不同的数据页里，也即是查一次数据会经历24次磁盘IO。

因此存放同样量级的数据，B+树的高度比跳表的要少，如果放在mysql数据库上来说，就是磁盘IO次数更少，因此B+树查询更快。

而针对写操作，B+树需要拆分合并索引数据页，跳表则独立插入，并根据随机函数确定层数，没有旋转和维持平衡的开销，因此跳表的写入性能会比B+树要好。

其实，mysql的存储引擎是可以换的，以前是myisam，后来才有的innodb，它们底层索引用的都是B+树。也就是说，你完全可以造一个索引为跳表的存储引擎装到mysql里。事实上，facebook造了个rocksDB的存储引擎，里面就用了跳表。

直接说结论，它的写入性能确实是比innodb要好，但读性能确实比innodb要差不少。感兴趣的话，可以在文章最后面的参考资料里看到他们的性能对比数据。

redis为什么使用跳表而不使用B+树或二叉树呢？

redis支持多种数据结构，里面有个有序集合，也叫ZSET。内部实现就是跳表。那为什么要用跳表而不用B+树等结构呢？

这个几乎每次面试都要被问一下。

虽然已经很熟了，但每次都要装作之前没想过，现场思考一下才知道答案。

真的，很考验演技。

大家知道，redis 是纯纯的内存数据库。

进行读写数据都是操作内存，跟磁盘没啥关系，因此也不存在磁盘IO了，所以层高就不再是跳表的劣势了。

并且前面也提到B+树是有一系列合并拆分操作的，换成红黑树或者其他AVL树的话也是各种旋转，目的也是为了保持树的平衡。

而跳表插入数据时，只需要随机一下，就知道自己要不要往上加索引，根本不用考虑前后结点的感受，也就少了旋转平衡的开销。

因此，redis选了跳表，而不是B+树。

总结

• B+树是多叉平衡搜索树，扇出高，只需要3层左右就能存放2kw左右的数据，同样情况下跳表则需要24层左右，假设层高对应磁盘IO，那么B+树的读性能会比跳表要好，因此mysql选了B+树做索引。

• redis的读写全在内存里进行操作，不涉及磁盘IO，同时跳表实现简单，相比B+树、AVL树、少了旋转树结构的开销，因此redis使用跳表来实现ZSET，而不是树结构。

• 存储引擎RocksDB内部使用了跳表，对比使用B+树的innodb，虽然写性能更好，但读性能属实差了些。在读多写少的场景下，B+树依旧YYDS。

参考资料

《MYSQL内核：INNODB存储引擎 卷1》

《RocksDB和Innodb引擎性能PK胜负难料？》